Если плоскость пересекает поверхность прямого кругового цилиндра (7 видео)

Содержание

Сечения цилиндра. Любая плоскость может пересекать поверхность прямого кругового цилиндра:
Пересечение цилиндра проецирующей плоскостью
Пересечение цилиндра плоскостью
Пересечение поверхностей плоскостями
🎬 Видео

Видео:Точка, линия на поверхности прямого кругового цилиндра. Сечение плоскостью наклонного цилиндра.Скачать

Сечения цилиндра. Любая плоскость может пересекать поверхность прямого кругового цилиндра:

Любая плоскость может пересекать поверхность прямого кругового цилиндра:

по окружности, если плоскость сечения перпендикулярна его образующим (рис.30);

по двум образующим, если секущая плоскость параллельна оси цилиндра и отстоит от неё на расстоянии, которое меньше радиуса цилиндра (рис.31);

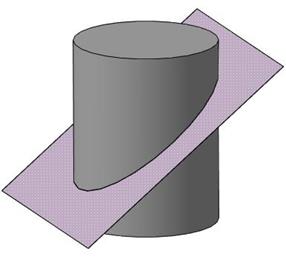
по эллипсу, если секущая плоскость наклонена к оси цилиндра и пересекает все его образующие (рис.32). Натуральная величина большой оси эллипса равна отрезку А₂В₂ следа секущей плоскости, заключённому между фронтальными очерковыми образующими цилиндра. Малая ось CD равна диаметру цилиндрической поверхности. Фронтальной проекцией фигуры сечения является отрезок А₂В₂, горизонтальной – окружность, профильной – эллипс. Для построения профильной проекции эллипса определяем достаточное количество промежуточных точек – 1, 2, 3 и 4.

Опорные точки А и В являются точками видимости на П₂, т.к. расположены на фронтальном очерке поверхности, и одновременно экстремальными относительно плоскостей проекций П₁ и П₃. опорные точки С и D являются точками видимости на П₃, поскольку расположены на профильном очерке, и экстремальными относительно фронтальной плоскости проекций.

Для того, чтобы найти натуральный размер эллипса, полученный в результате сечения цилиндра плоскостью, проводим параллельно фронтальной проекции плоскости сечения α ось Х. На эту ось переносим все точки сечения 1,2,3 и т.д., через которые проводим прямые перпендикулярные оси, и от этих точек откладываем расстояния, равные расстояниям от оси симметрии на горизонтальной проекции до точек окружности. Получим точки, принадлежащие фигуре сечения, т. е. эллипсу.

На рис.33 построены три проекции цилиндра, усечённого плоскостью β. Плоскость пересекает основание цилиндра по прямой, поэтому фигурой сечения является неполный эллипс. Большая ось эллипса определяется отрезком А₂В₂, малая CD равна диаметру цилиндра. Для наглядности плоский срез цилиндра показан на чертеже заштрихованным. Дано изображение натуральной величины фигуры сечения.

Видео:Построение линии пересечения поверхности конуса с проецирующей плоскостьюСкачать

Пересечение цилиндра проецирующей плоскостью

Если прямой круговой цилиндр рассечь плоскостью, параллельной его основаниям, то линия пересечения боковой поверхности с этой плоскостью будет окружность (рис. 282, а).

Если цилиндр рассечь наклонной плоскостью так, чтобы пересеклись все его образующие, то линия пересечения боковой поверхности с этой плоскостью будет эллипсом, величина и форма которого зависят от угла наклона секущей плоскости к плоскостям оснований цилиндра (рис. 282, б).

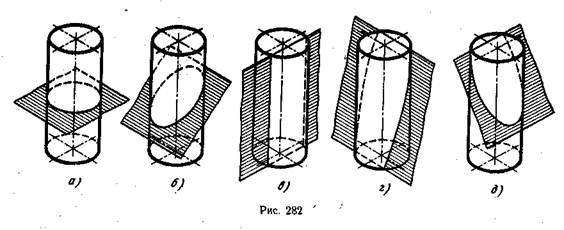Если плоскость пересекает поверхность прямого кругового цилиндра

Если цилиндр рассечь плоскостью, перпендикулярной к его основаниям, линия пересечения боковой поверхности с этой плоскостью будет прямоугольником (рис. 282, в).

Читайте также: Цилиндр для замка 30х50 с вертушкой

Если цилиндр рассечь наклонной плоскостью так, что она пересечет основания и боковую поверхность, то линия пересечения будет частью эллипса, отсеченной двумя хордами оснований (рис. 282, г).

Если секущая плоскость пересечет одно основание и часть боковой поверхности, то линия пересечения боковой поверхности с этой плоскостью будет частью эллипса отсеченного одной хордой основания (рис. 282, д).

Видео:Построение линии пересечения поверхности цилиндра с проецирующей плоскостиСкачать

Пересечение цилиндра плоскостью

Линией пересечения поверхности цилиндра плоскостью может быть окружность, две образующие, эллипс.

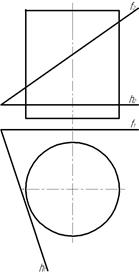
Пример 1. Построить линию пересечения цилиндра плоскостью α(f∩h) (рис. 97).

Линией пересечения прямой круговой цилиндрической поверхности плоскостью общего положения является эллипс. Данная цилиндрическая поверхность является горизонтально-проецирующей, так как ее образующие перпендикулярны горизонтальной плоскости проекций. Следовательно, линия пересечения, как принадлежащая такой поверхности, на горизонтальную плоскость проекций проецируется в виде очерка этой поверхности, т. е. в виде окружности. На фронтальную плоскость проекций линия пересечения проецируется в виде эллипса.

Точки эллипса построены по принадлежности их плоскости α(h∩f) при помощи фронталей. Фронтальные проекции точек С и K отделяют видимую часть эллипса от невидимой части (рис. 98).

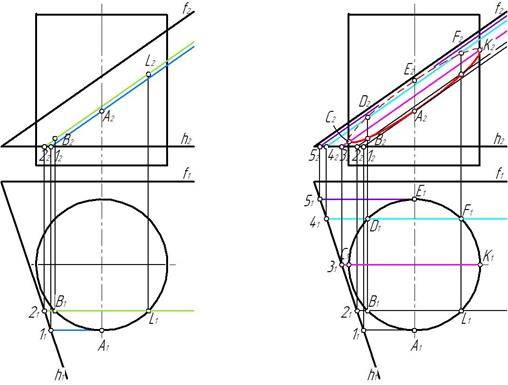
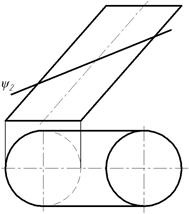
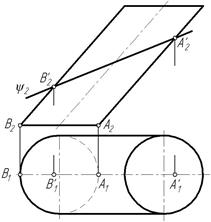
Пример 2. Построить линию пересечения наклонного цилиндра с фронтально-проецирующей плоскостью ψ( ψ₂) (рис. 99).

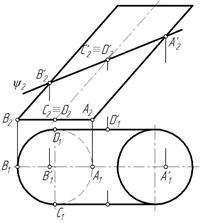
Линией пересечения плоскости ψ с поверхностью цилиндра будет эллипс. Фронтальная проекция эллипса совпадает с фронтальной проекцией плоскости ψ₂.

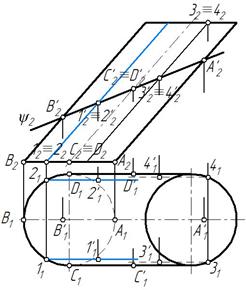
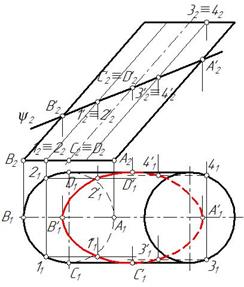
Горизонтальную проекцию эллипса построим по точкам. Определяем проекции характерных точек, находящихся на очерковых образующих.

Это проекции точек А‘, В‘, С‘, D‘ (рис. 100). Затем отмечаем две произвольные точки 1‘ и 2‘, принадлежащие образующим цилиндра 1 и 2 и плоскости ψ, а также точки 3 и 4. Полученные точки соединяем плавной кривой с учетом видимости. Точки 1′₁, 2′₁, В’₁, С’₁, D ‘₁ принадлежат видимым образующим, следовательно они видимы. На очерковых образующих в точках С’₁ и D ‘₁ меняется видимость, т. е. эллипс становится невидимым (рис. 101).

Пересечение пирамиды плоскостью

Линия пересечения поверхности многогранника плоскостью будет плоская ломаная линия,состоящая из звеньев прямых.

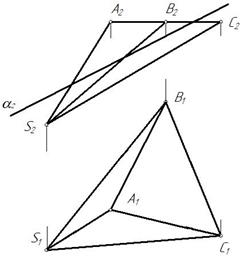
Пример 1. Построить линию пересечения пирамиды фронтально-проецирующей плоскостью α(α₂) (рис. 102).

Фронтально-проецирующая плоскость пересекает основание пирамиды АВС в точках 3 и 4. Ребра SА и SB плоскость пересекает в точках 1 и 2 соответственно. Строим проекции точек 1, 2,3 и 4 и соединяем их горизонтальные проекции с учетом видимости. Грань ВSС невидима относительно плоскости проекций П₁, следовательно, прямая 2₁ 3₁ невидима (рис. 103).

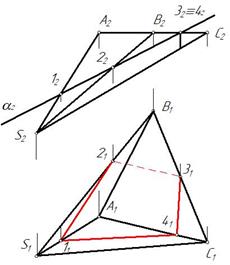
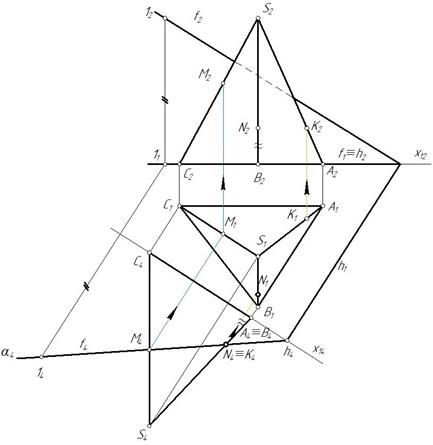
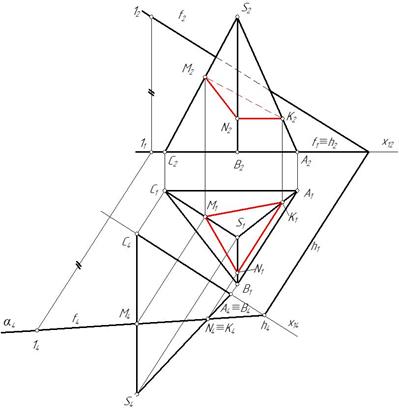
Пример 2. Построить линию пересечения пирамиды плоскостью α(f∩h) (рис. 104).

Читайте также: Прямой круговой цилиндр это фигура

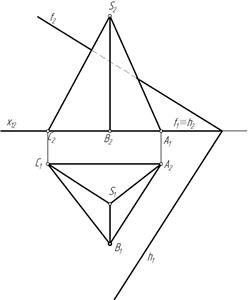
Линией пересечения трехгранной пирамиды с плоскостью будет треугольник,точки которого принадлежат ребрам пирамиды. Поскольку ребро SA является профильной прямой задачу целесообразно решать при помощи дополнительного ортогонального проецирования.

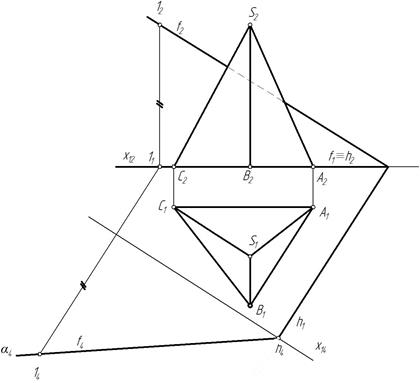
Преобразуем плоскость α(h∩f) из общего положения в частное, для этого построим дополнительную ортогональную проекцию плоскости α на плоскость ей перпендикулярную. П₄^α и П₄^П₁ (рис. 105). Проводим ось х₁₄ ^ h₁ и строим дополнительную проекцию плоскости и пирамиды.

На фронтали отмечаем произвольную точку 1, строим дополнительную проекцию 1₄, горизонталь спроецируется в точку. Плоскость спроецируется в прямую α₄. Строим также дополнительную ортогональную проекцию пирамиды. На пересечении с проекциями ребер пирамиды отмечаем дополнительные проекции точек М₄, N_4, K₄ (рис. 106).

Затем находим горизонтальные и фронтальные проекции этих точек и соединяем их с учетом видимости (рис. 107). Грань АSC не видима относительно плоскости проекций П₂, прямая K ₂ М₂ не видима.

Дата добавления: 2019-09-13 ; просмотров: 904 ; Мы поможем в написании вашей работы!

Видео:Лекция #13Скачать

Пересечение поверхностей плоскостями

Форму деталей часто образуют срезом или вырезом части материала плоскостями из исходных тел — заготовок, ограниченных криволинейными поверхностями. При этом возникает необходимость построения на чертеже проекций линии пересечения поверхности плоскостью. Такие же линии строят на чертежах деталей, поверхности которых ограничены пересекающимися между собой участками плоскости и поверхности.

В случае пересечения линейчатой поверхности плоскостью линия пересечения может быть кривой или прямой.

Для построения линии пересечения линейчатой поверхности плоскостью в общем случае строят точки пересечения прямолинейных образующих поверхности с секущей плоскостью, т. е. находят точки пересечения прямой с плоскостью. Искомую кривую проводят через эти точки.

Для построения линии пересечения линейчатой поверхности с плоскостью в общем случае применяют вспомогательные секущие плоскости. Точки искомой линии определяются в пересечении линий, по которым вспомогательные секущие плоскости пересекают данные поверхность и плоскость. Примеры применения вспомогательных плоскостей рассмотрены ниже.

При подборе вспомогательных плоскостей надо стремиться к упрощению построений. Если секущая плоскость — плоскость частного положения, то задача упрощается, так как одна проекция линии пересечения плоскости с кривой поверхностью уже имеется и совпадает со следом секущей плоскости. Построение недостающих проекций линии пересечения сводится к построению недостающих проекций точек на поверхности по заданным проекциям этих точек на одной из проекций поверхности.

Пересечение цилиндрической поверхности плоскостью.Для построения линии пересечения цилиндрической поверхности плоскостью в общем случае находят точки пересечения образующих с секущей плоскостью. При необходимости не исключается применение и вспомогательных секущих плоскостей, пересекающих поверхность и плоскость.

Читайте также: Может ли повести чугунный блок цилиндров от перегрева

Заметим, что любую цилиндрическую поверхность плоскость, расположенная параллельно образующей этой поверхности, пересекает по прямым линиям (образующим).

Вид линии, образованной при пересечении плоскостью прямого кругового цилиндра, определяется положением плоскости относительно оси. Эта линия — окружность, если плоскость перпендикулярна оси; две прямые (проекции 1’2′ и 3’4′ на рисунке 75) или одна прямая (касательная), если плоскость параллельна оси (след P_w); эллипс (1—2—3—4 на рисунке 76), если плоскость расположена под углом к оси.

Образование выреза на цилиндре двумя плоскостями Р (P_v) || W и T(T_W) || V показано на рисунке 76.


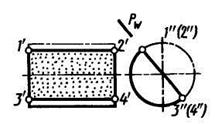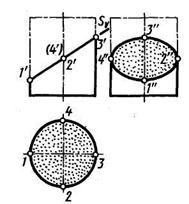Рисунок 75	Рисунок 76	Рисунок 77

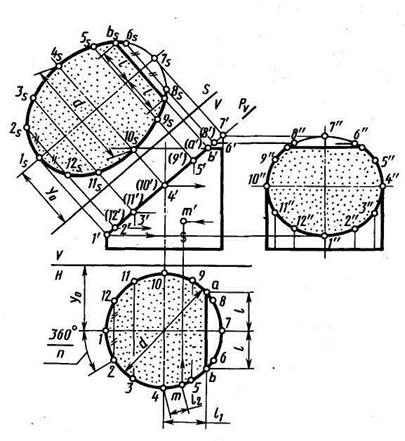
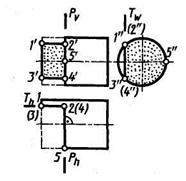
Цилиндр с наклонным срезом.Рассмотрим построение чертежа цилиндра со срезом проецирующей плоскостью под некоторым углом к его оси (не равным 0° и 90°), натуральной величины среза (рисунок 78).

Ось цилиндра и вся цилиндрическая поверхность перпендикулярны плоскости Н. Следовательно, все точки цилиндрической поверхности, в том числе и линия пересечения ее с плоскостью Р (P_v) проецируются на плоскость Н в окружность. На ней отмечают горизонтальные проекции точек 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 и 12 эллипса, расположив их равномерно по окружности. В проекционной связи строят фронтальные проекции 1′, 2′, 3′, 4′, 5′, 6′, 7′, 8′, 9′, 10′, 11′ и 12′ отмеченных точек на фронтальном следе Р_V, секущей плоскости. Профильные проекции тех же точек строят по их горизонтальной и фронтальной проекциям на линиях связи.

Профильная проекция линии пересечения цилиндра с секущей плоскостью – эллипс, большая ось 10″4″ которого в данном случае равна диаметру цилиндра, а малая 1″7″ — профильная проекция отрезка 1—7.

Натуральный вид фигуры сечения цилиндра плоскостью Р построен способом перемены плоскостей проекций на плоскости S, перпендикулярной плоскости V.

Пересечение конической поверхности плоскостью.При пересечении конической поверхности вращения плоскостью получаются различные линии — прямые, замкнутые кривые — окружности и эллипсы, незамкнутые кривые — параболы и гиперболы, а также точка. Вид указанных линий определяется положением секущей плоскости относительно вершины конической поверхности и соотношением между величинами углов наклона секущей плоскости и образующей конической поверхности к ее оси.

Если секущая плоскость Р (P_v) проходит через вершину (рисунок 79, а), то пересечение плоскости с конической поверхностью в зависимости от угла α наклона плоскости к оси поверхности образует: