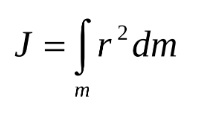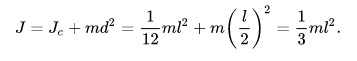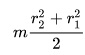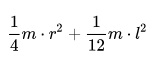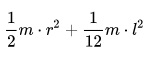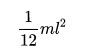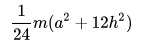Любая электромеханическая система включает, как правило, элементы вращательного и поступательного движения, как правило, от электродвигателя к рабочему органу механизма. Циклы работы электропривода состоит из пуска и разгона системы, установившегося режима, и замедления до полной остановки. Для расчета режимов работы необходимо определить моменты инерции передаточного механизма. Значения моментов инерции простейших геометрических тел приведены ниже. Следует отметить, что момент инерции
, где маховый момент.
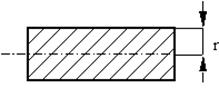
сплошной цилиндр
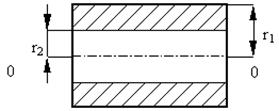
полый цилиндр
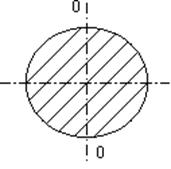
| стержень вращается вокруг оси 0_0 |
Задача 2.1.Компрессор приводится в движение двигателем типа АК-112-8 с номинальными данными: Uном=380В; Рном=160кВт; nном=735об/мин. Вал двигателя непосредственно соединен с валом компрессора и маховиком (рисунок 2.1). Момент инерции соединительной муфты и коленчатого вала составляют соответственно 5% и 3% от момента инерции маховика. Материал маховика – чугун с удельным весом γ=7,5 т/м³.Определить момент инерции привода.
1) Определяем массу маховика без пустот
2) Находим возможный момент инерции осевой пустоты
3) Определяем возможный момент инерции полых выемок
Поскольку таких выемок в маховике две, суммарный момент инерции равен .
Задача 2.2. Электродвигатель с маховым моментом GD²=20кг∙м² и маховиком разгоняется до частоты вращения 1500об/мин (рисунок 2.2). Определить момент инерции и время разгона двигателя с пусковым моментом Мп =400Н∙м. Материал маховика – сталь с удельным весом γ=7,8т/м³, решить самостоятельно.
Задача 2.3.Электродвигатель с маховым моментом GD²=10кг∙м² и маховиком разгоняется до частоты вращения 1000об/мин (рисунок 2.3). Определить момент инерции и время разгона двигателя с пусковым моментом Мп =300Н∙м. Материал маховика – сталь с удельным весом γ=7,8т/м³.
Большинство судовых механизмов работают при малых скоростях рабочего органа, тогда как электродвигатели имеют частоту вращения до 3000 об/мин. Поэтому вал электродвигателя соединяется с рабочим органом механизма с помощью редуктора. Для исследования процессов и определения параметров системы её заменяют одним эквивалентным звеном. Такая система называетсяприведенной.Элементы вращательного и поступательного движения приводятся к валу двигателя.
Задача 2.4.Механизм подъема мостового крана имеет следующие характеристики: Z1=Z3=10; Z2=Z4=50; nд=1500об/мин; Dб=0,6м; G=1,5т; GD0²=1,5 кг∙м²; GD1²=2 кг∙м²; GD2²=20 кг∙м² (рисунок 2.4). Определить приведенный к валу двигателя момент инерции, приняв для упрощения к.п.д. равным 100%.
Учитывая, что: определяем
Угловая частота двигателя:
Приведенный момент инерции элементов вращательного движения
Приведенный радиус инерции
Если в реальных условиях принять к.п.д. шестеренок η1=η2=0,95 ; барабан-канат η3=0,95; блок-канат η4=0,95, тогда будем иметь
Читайте также: При перезарядки тм выше давления включения компрессора
Силы и моменты, действующие
В системе электропривода.
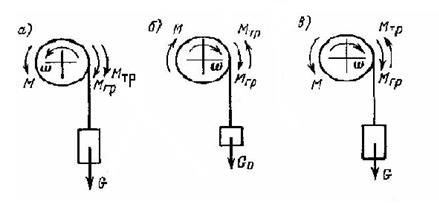
Соотношение статических моментов, преодолеваемых двигателем лебедки при подъеме и спуске одного и того же груза (рис.3.1а).
Рисунок 3.1(а) – Взаимодействие моментов, действующих на вал.
Рисунок 3.1(б) – Абсолютное значение статического момента:
Вычтя из первого уравнения второе, получим (рисунке 3.1.б)
Это соотношение моментов справедливо при расчете грузоподъемных механизмов электроприводов.
Задача 3.2. Определить статические моменты на валу двигателя грузовой трехтонной лебедки при подъеме и спуске номинального груза и холостого гака, если масса холостого гака m0=60кг; диаметр грузового барабана Dб=400мм; передаточное отношение редуктора i=23,3; КПД механизма при подъеме номинального груза η=0,8.
1.Загрузка механизма при подъеме холостого гака Fx/Fн=m0/mн=60/3000=0,02 соответствует КПД (рисунок 3.2) η0=0,15.
2. Статические моменты (на валу двигателя):
при подъеме номинального груза
при спуске номинального груза
при подъеме холостого гака
при спуске холостого гака
Рисунок 3.2. – Зависимость КПД зубчатых передач η от загрузки механизма
Задача 3.3.Определить время, за которое двигатель лебедки (данные смотри в задаче 3.1.) под действием неизменного пускового момента Мп=450 Н∙м разгонится при подъеме и спуске номинального груза до скорости ωст=97 рад/с и остановится после отключения от сети и наложения тормоза с Мт=2Мст2. Момент инерции двигателя Jдв=1,9 кг∙м². Инерционность передачи и грузового барабана учитываем введением коэффициента k=1,2. Скорость подъема и спуска груза υ=50 м/мин. (В реальных условиях эти скорости определяют из механической характеристики двигателя в соответствии с Мст.).
Решение:Приведенный момент инерции электромеханической системы
Видео:Расчёт момента инерции тела относительно оси вращения. Момент инерции однородного стержняСкачать

Физический смысл момента инерции
Когда тело продолжает двигаться при отсутствии на него воздействия каких-либо сил, говорят о проявлении инерции. Именно ею объясняются трудности удержаться на ногах при резком торможении автобуса или усидеть в седле велосипеда, когда под колеса резко выбегает кот. Кроме инерции, проявляющейся при движении тел по прямой, аналогичное явление бывает при вращении вокруг оси. В таком случае в физике говорят о моменте инерции – скалярной величине, измеряющей инертность тела при осевом вращении.
Видео:Момент инерцииСкачать

Момент инерции и его физический смысл
Обеспечить поступательное движение предмета при его толкании будет тем тяжелее, чем больше он весит. Аналогичные эксперименты предусматривались школьной программой и относились к прямо направленному действию.
Было понятно, что именно масса тела характеризует степень его инертности и является ее мерой.
Читайте также: Кулачковых валов дизеля 10д100
При совершении предметом вращательных движений наблюдается иной вид зависимости. В данном случае мерой инертности выступает момент инерции.
Момент инерции – скалярная измеряемая характеристика инертности тела в момент совершения осевого вращения.
Задачи по определению величины момента инерции решаются с помощью теоремы Гюйгенса-Штейнера, смысл которой заключается в следующем:
МИ для тела, вращающегося вокруг какой-либо оси, равна сумме слагаемых единиц: момент инерции предмета, который вращается вокруг оси, параллельной данной, и проходящей через центр масс, а также произведения массы на расстояние между осями, возведенное в квадрат.
В приведенной формуле используются следующие обозначения: d – расстояние между осями, m – масса тела, Iz – момент инерции относительно рассматриваемой оси, а Ic – относительно оси, которая проходит через центр масс. В профильной литературе и учебниках буква I может заменяться J.
Формулировка способа количественного измерения момента инерции при осевом вращении предмета стала возможной в результате работы двух ученых-математиков: Гюйгенса и Штейнера. Теорема дает возможность быстрого решения задач на определение инерции предмета любой формы, для которого уже просчитана центробежная сила. Формула Штейнера позволяет вычислить момент инерции этого предмета относительно выбранной оси, проходящей параллельно прямой, следующей через центр фигуры.
Видео:Геометрические характеристики. Моменты инерции. Радиусы инерции. Сопромат.Скачать

Единицы измерения в системе СИ
Единицей измерения момента инерции, принятой в системе СИ, является кг, умноженный на метр в квадрате — кг·м². В еще одной системе измерения (СГС) единицей измерения является грамм на квадратный сантиметр — г·см².
Видео:Урок 94. Вычисление моментов инерции телСкачать

Как рассчитать момент инерции, формула
Измерение значения момента инерции можно произвести теоретически, согласно формуле. Для этого условно движущийся предмет разбивается на мелкие составляющие, масса которых обозначается dm. В конечном итоге момент инерции (МИ) равняется сумме произведений всех образовавшихся масс на расстояние до оси, возведенное в квадрат.
Исходя из этой формулы, момент инерции, кроме массы тела, определяется положением оси, вокруг которой предмет вращается, а также его формой и габаритами.
Возможность рассчитать моменты инерции полезна, к примеру, при исследованиях свойств и структуры элементов Солнечной системы. Это так называемый безразмерный момент инерции. Высчитанная по формуле величина дает представление о распределении массы по глубине.
Видео:Вычисление моментов инерции составного сеченияСкачать

Виды моментов инерции
Кроме безразмерного момента инерции, в физике существуют понятия:
- центробежный МИ;
- главный МИ;
- геометрический МИ;
- МИ относительно плоскости;
- центральный МИ;
- тензор инерции;
- эллипсоид инерции.
Центробежными МИ относительно прямоугольных осей координат (декартовой системы) считаются Jxy, Jxz, Jyz. Ось ОХ является главной, когда центробежные моменты инерций Jxy и Jxz равняются нулям.
Читайте также: Правка центровых отверстий вала
Любая точка тела может являться центром трех главных осей инерции. Они характеризуются взаимной перпендикулярностью. МИ относительно них считается главным для данного предмета. Главные оси, которые пролегают через центр масс, — являются главными центральными осями инерции предмета. МИ относительно них – главные центральные МИ. Для однородного тела ось симметрии всегда является главной центральной осью инерции.
Для геометрических МИ существуют формулы, основывающиеся на объеме относительно оси и площади относительно оси.
Твердое тело может иметь МИ относительно плоскости. Тогда это – скалярная величина, которая рассчитывается суммированием произведений массы каждой точки предмета и расстояния от нее до плоскости, возведенного в квадрат.
Понятие «Центрального МИ» связано с точкой О, МИ относительно полюса либо полярным МИ.
Видео:Определение момента инерции сеченияСкачать

Момент инерции тела относительно оси вращения
МИ служит единицей измерения инерции тела, которое вращается вокруг оси, подобно тому, как масса является мерой при поступательном движении.
Определить МИ предметов касательно оси вращения позволяет формула Штейнера.
Наглядное подтверждение применения формулы Штейнера – расчет МИ стержня, ось вращения которого проходит через конец.
Видео:Нахождение момента инерции стержня путем интегрированияСкачать

Моменты инерции простейших объектов
Момент инерции некоторых однородных тел, имеющих простую форму, в зависимости от характеристик осей вращения можно определить по следующим формулам:
- МИ точечного предмета либо полого цилиндра с тонкими стенками (с массой m и радиусом r) = mr 2
- МИ диска или сплошного цилиндра = 1/2 mr 2
- МИ цилиндра с толстыми стенками, у которого внешний радиус обозначен r2, а внутренний – r1, :
Видео:Определение осевых моментов инерции составного несимметричного сечения. СопроматСкачать

Примеры решения задач
Применение на практике приведенных формул происходит, например, для решения следующих задач. Задано найти МИ однородного диска с известными массой и радиусом. Из дополнительных сведений: ось вращения – через центр диска. Для решения диск разбивается на тонкие кольца, радиусы которых равняются от 0 до R. Взяв одно из них и обозначив его радиус буквой \(r\) , а массу – \(dm\) , формула для расчета МИ (согласно теореме Гюйгенса-Штейнера) выглядит следующим образом: \(dJ=dmr2.\) С учетом подстановки в конечную формулу для определения МИ формулы для массы кольца получаем: 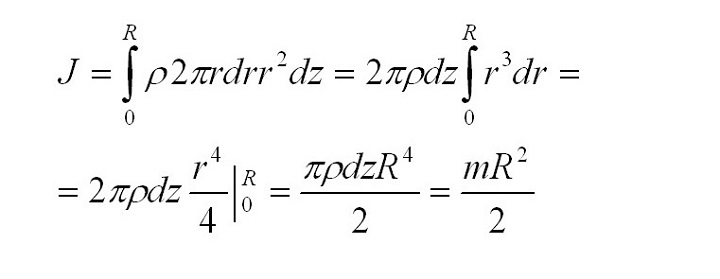
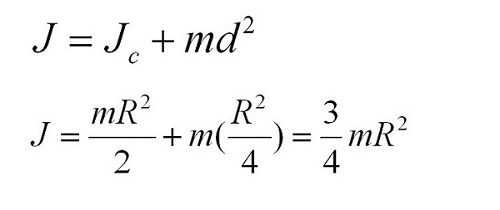
- Свежие записи
- Чем отличается двухтактный мотор от четырехтактного
- Сколько масла заливать в редуктор мотоблока
- Какие моторы бывают у стиральных машин
- Какие валы отсутствуют в двухвальной кпп
- Как снять стопорную шайбу с вала
- Правообладателям
- Политика конфиденциальности
📹 Видео
Определение момента инерции и разгон с рассчитанным темпомСкачать
Расчет момента инерции тонкого стержняСкачать
Определение моментов инерции твёрдых тел методом крутильных колебаний (лабораторная работа М30)Скачать
КРУЧЕНИЕ ВАЛА. Касательные напряжения. Сопромат.Скачать
Моменты инерции Прямоугольника ► Вывод моментов инерции для прямоугольникаСкачать
Техническая механика/Определение общих осевых моментов инерции сложносоставного сечения.Скачать
Момент силы относительно точки и осиСкачать
#1 определение момента инерции кольца методом колебанийСкачать
Кручение. Расчет составного вала кольцевого сечения.Скачать
2 а Моменты инерции сферы и шараСкачать
Момент инерции абсолютно твердого тела. 10 класс.Скачать