Формула для расчета прочности вала (7 видео)

Валы применяются во многих механизмах для передачи вращающего момента от одной детали к другой. Как правило, расчетная нагрузка для вала в виде внешнего крутящего момента М определяется исходя из передаваемой мощности Nи заданной угловой скорости ωвращения вала:

ω – угловая скорость в рад/с.

С использованием других единиц мощности и/или скорости вращения вала в формуле (2.13) появляется числовой коэффициент. Например, часто применяется такая формула:

n – скорость вращения вала, об/мин.

Для обеспечения работоспособности валы должны удовлетворять условиям прочности и жесткости. Для расчета вала на прочность необходимо знать наибольшие касательные напряжения в сечениях вала от действующей нагрузки, для расчета на жесткость – наибольшие относительные углы закручивания.

На практике применяются валы гладкие (постоянного сечения) и ступенчатые. В случае ступенчатого вала необходимо получить расчетные касательные напряжения и относительные углы закручивания на каждом участке постоянного сечения, а затем выбрать из них соответствующие наибольшие значения.

Условие прочности вала из пластичного материала имеет вид:

гдеτmax- наибольшие касательные напряжения для вала в целом;

[τ] — допускаемое напряжение вала при кручении ;

τ_T – предел текучести материала при кручении;

n_T— коэффициент запаса по текучести.

Касательные напряжения для каждого участка вала вычисляются по формуле (3.2).

Величина допускаемого напряжения зависит от различных факторов, но в основном от материала вала. Для пластичных материалов можно принимать .

При проведении проектировочного расчета вала определяются размеры поперечных сечений вала с использованием условия прочности (3.15) и формул (3.2), (3.4), (3.6):

Здесь значение крутящего момента М_к и выражение для полярного момента сопротивления W_pподставляются для опасного сечения, т.е. для поперечного сечения на участке вала, где действуют наибольшие касательные напряженияτmax.

Условие жесткостидля вала имеет вид:

где – наибольшее значение относительного угла закручивания для вала;

– допускаемый относительный угол закручивания для вала.

Для валов различного назначения [φ]΄=(0,25−0,3) град/м.

Следует обратить внимание, что в формулу (3.17) значение[φ]΄подставляется в радианах в секунду. Для перевода градусов в радианы нужно воспользоваться преобразованием

Расчет вала на жесткость может быть не только проверочным, но и проектировочным, т.е. служить для определения размеров сечения. Так, при расчете вала на жесткость можно определить необходимое значение диаметра из условия (3.17)):

Здесь значение крутящего момента М_к и выражение для полярного момента инерции J_pподставляются для поперечного сечения на участке вала.где возникает наибольший относительный угол закручивания .

При совместном расчете вала на прочность и жесткость для определения величины диаметра вала расчетных значений, полученных по формулам (3.16) и (3.18), выбирается наибольшее, чтобы выполнялись оба условия – прочности и жесткости.

Содержание

Расчет валов на прочность и жесткость при кручении
Расчет валов на прочность и жесткость при кручении
5.5. Расчет валов на жесткость
📹 Видео

Видео:КРУЧЕНИЕ ВАЛА. Касательные напряжения. Сопромат.Скачать

Расчет валов на прочность и жесткость при кручении

Видео:Расчет вала на прочность и жесткость. Эпюра крутящих моментовСкачать

Расчет валов на прочность и жесткость при кручении

Расчет вала на прочность И жесткость на кручение Для своей конструкции можно рекомендовать следующий порядок расчета вала на прочность и жесткость при кручении. По схеме вала и действующему на него крутящему моменту строится график

крутящего момента для отдельных участков (§ 16). Выберите материал расчетного вала и определите допустимое напряжение[t] для этого материала. Условия записи Секционная прочность 214 вала с максимальным значением крутящего момента(согласно диаграмме крутящего момента) (9.12).

Если вал достаточно длинный и отдельные секции достаточно сильно отличаются по величине крутящего Людмила Фирмаль

момента, то они должны быть ступенчато спроектированы. Диаметр вала каждой ступени рассчитывается по одной и той же формуле(9.12), но значения крутящего момента различны для разных участков в зависимости от графика крутящего момента. Учитывая, что можно написать формулу для расчета диаметра вала

из сплошного круглого вала Wp=уравнение (9.13: (9.16) Определить диаметр полой оси, заданный соотношением между размерами внутреннего и наружного диаметров из конструктивных соображений, т. е. коэффициент= — тогда, учитывая уравнение(9.11), из уравнения (9.13)следует:: (9.17)) После определения размеров вала из условий прочности проверьте жесткость вала по формуле (9.14).

Допустимый относительный угол поворота вала составляет 0,3°для каждого метра статической нагрузки[0′] — длина вала, переменная нагрузка[0°1=0,25°, ударная нагрузка[0 ′ 4=0,15°]. Учитывая, что формула (9.14) представляет угол закрутки в радианах, значение данного допустимого угла преобразуется в радианы, и в испытании выполняется условие жесткости (9.14), в противном случае размеры вала должны выбираться из условия жесткости(9.15).): Подставляя в эту формулу формулу момента полярной инерции, находим ее для непрерывной оси (9.18) Для полого вала Иногда при расчете вала

известно, что передаваемая мощность n равна лошадиным силам, а число оборотов-n в минуту. В этом деле 21 крутящий момент формулы может быть выражен непосредственно в терминах мощности n и числа оборотов n, исходя из Формулы (3.1): МК=71 620-кгс*(9.20) мощность/(задается в киловаттах, когда крутящий момент определяется по формуле (3.2): МК-97 360-кгс * см.(9.21）) >

27, например. Найти мощность, передаваемую валом, диаметр Людмила Фирмаль

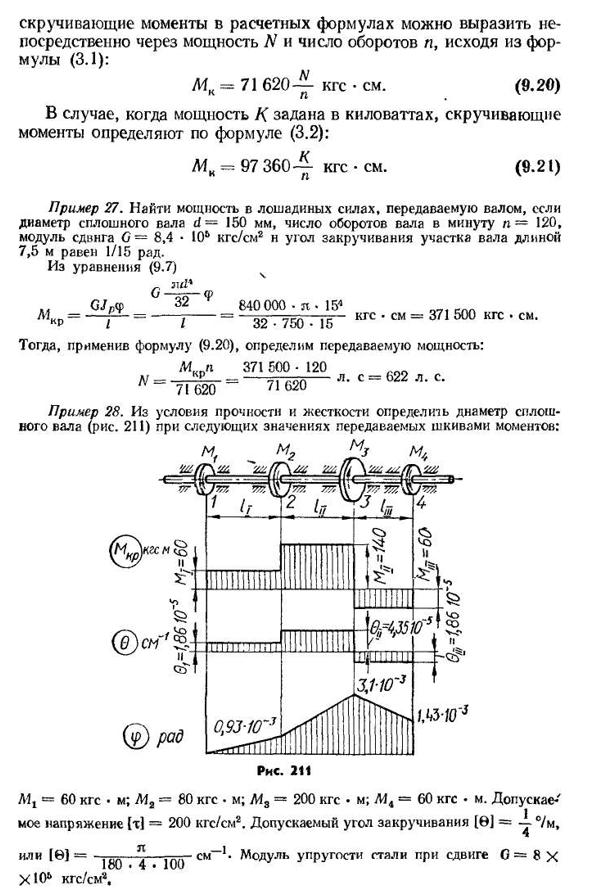
сплошного вала d-150мм, число оборотов вала n-120 в минуту, модуль сдвига G— 8,4 • 10 длина участка оси кгс / см2н с углом кручения 7,5 м составляет 1/15 Радиана. Из уравнения(9.7) И ой.. GJpat/7=/7 / =50 см h=J=90 см. В этом случае одна из секций фиксируется (рис. 211 настоящего раздела/). В пределах каждой секции 0-const угол кручения каждой секции изменяется по линейному закону,B, MD. Max=M V и формула на основе L\ymk В (А+Б) л[т] *

Видео:9.1 Расчет валов приводаСкачать

5.5. Расчет валов на жесткость

5.5. РАСЧЕТ ВАЛОВ НА ЖЕСТКОСТЬ

За меру жесткости принимают относительный угол закручивания, то есть угол, приходящийся на единицу длины вала Условие жесткости: ≤ [θ] где [θ] имеет размерность рад/м. Чаще пользуются условием Допускаемое значение угла [θ°] закручивания зависит от назначения вала. Принимают [θ°] = (0,3–1,0) град/м. При расчете валов на прочность и жесткость часто задают мощность N, передаваемую валом и частоту его вращения n. Для вычисления крутящего момента по этим данным удобно воспользоваться таблицей Пример 5.1. Расчета вала на прочность и жесткость I. Определение внутренних усилий Значение ведущего момента Мвед определим из условия равновесия вала: Σ Мх = 0; Мвед – М1 – М2 – М3 = 0, откуда Мвед = М1 + М2 + М3 = 5 + 7 + 6 = 18 кН·м. Для расчетов на прочность и жесткость необходимо найти положение опасных сечений и величины крутящих моментов, действующих в этих сечениях вала (рис. 5.3, а). Воспользовавшись методом сечений определим внутренние усилия и построим эпюру крутящих моментов (рис. 5.3, б). Опасными являются все сечения на участке II, где действует Тmax = 12 кН·м. II. Проектный расчет валов сплошного и полого сечений Предварительно найдем допускаемое касательное напряжение, связанное с допускаемым нормальным напряжением. Принимаем по третьей теории прочности [τ] = 0,5 [σ] = 0,5·160 = 80 МПа. Из условия прочности и жесткости при кручении находим требуемые значения полярных момента сопротивления и момента инерции Из условия прочности и жесткости выполнить проектный расчет: определить диаметры валов в двух вариантах исполнения – сплошного и полого с коэффициентом пустотелости с = d/D = 0,8. Результаты округлить согласно ГОСТу. Построить эпюры углов закручивания вала. Валы сопоставить по металлоемкости и жесткости. Дано: М1 = 5 кН·м; a = 0,6 м; М2 = 7 кН·м; b = 0,8 м; М3 = 6 кН·м; с = 0,7 м; [σ] = 160 МПа; [θ] = 0,8 град/м. Рис. 5.3. Схема нагружения вала (а), эпюра крутящих моментов (б), эпюры углов закручивания сплошного (в) и полого (г) валов Результаты расчетов Форма сечения Сплошное Полое Момент сопротивления Углы закручивания характерных сечений вала сплошного и полого сечений Момент инерции принятый Жесткость сечения G·Ip = 80·109·1,19·10-5 = 0,955·106 Н·м2 G·Ip = 80·109·1,20·10-5 = 0,961·106 Н·м2. Углы закручивания участков вала Углы закручивания характерных сечений вала Строим эпюры углов закручивания сплошного и полого валов (рис. 5.3, в и г) III. Сопоставление металлоемкости валов двух вариантов Металлоемкость вала определяется его объемом, то есть произведением длины на площадь поперечного сечения. Поскольку длина вала неизменна, сопоставим площади поперечных сечений сплошного вала с полым Выводы: 1. Из условий прочности и жесткости найдены диаметры вала двух вариантов исполнения, сплошного и пустотелого: 105 и 120 мм соответственно. 2. Вычислены деформации валов на каждом из участков, построены эпюры углов закручивания валов сплошного и пустотелого. Жесткости валов практически одинаковы. 3. Сопоставлены металлоемкости валов двух вариантов исполнения. Расход металла для вала сплошного сечения вдвое больше, чем для вала пустотелого. Примечание. Полученный результат по сопоставлению металлоемкости валов ожидаем, поскольку достаточно большой объем материала, сосредоточенный около центра тяжести сечения, испытывает напряжения ниже допускаемого и вклад его в общую прочность конструкции невелик. Поэтому целесообразно убирать неработающий материал из этой области. Конструкции из полого сечения созданы природой: камыш, тростник, бамбук, злаковые культуры, трубчатые кости птиц и млекопитающих. В авиации и космонавтике используют полые валы, в строительстве – пустотные плиты перекрытий.

источники:

https://evakuatorinfo.ru/formula-dlya-rascheta-prochnosti-vala