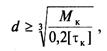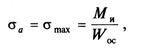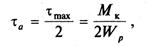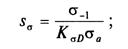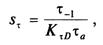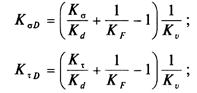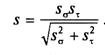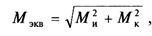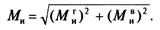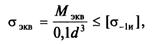скручивающих элементов машины работают на совместное действие кручения и изгиба. Эти детали имеют коленчатый вал. При расчете элементов, действующих одновременно на изгиб и кручение, сначала необходимо изучить расчетные значения изгибающих моментов
l1i и крутящего момента l4k. Это показано на примере прямой оси Людмила Фирмаль
круглого сечения со шкивом и кривошипом. Схема вала показана на рисунке. 443 и 444. Рассмотрим момент, когда натяжение ремня T и t на правом конце кривошипного пальца становится горизонтальной силой P, а кривошип становится вертикальным. Размеры конструкции можно найти на чертежах. Объявления, которые определяют изгиб и крутящий момент вала. Сила,
действующая на шкив T и t (натяжение ремня), заменяется силой T4-L, приложенной в центре колеса, а пара (T-t)R Q Ro является радиусом шкива. Сила Т4
Т, вместе с весом шкива к, произведет гнуть вала; РО пары (т—т), переплетая вал, сбалансировано парой приложенной к правому концу. Заменить силу Р, действующую на палец кривошипа, силой Р, приложенной к валу при продолжении оси точки М и парой моментов Р/G0. Таким образом, pH§и (T—t)
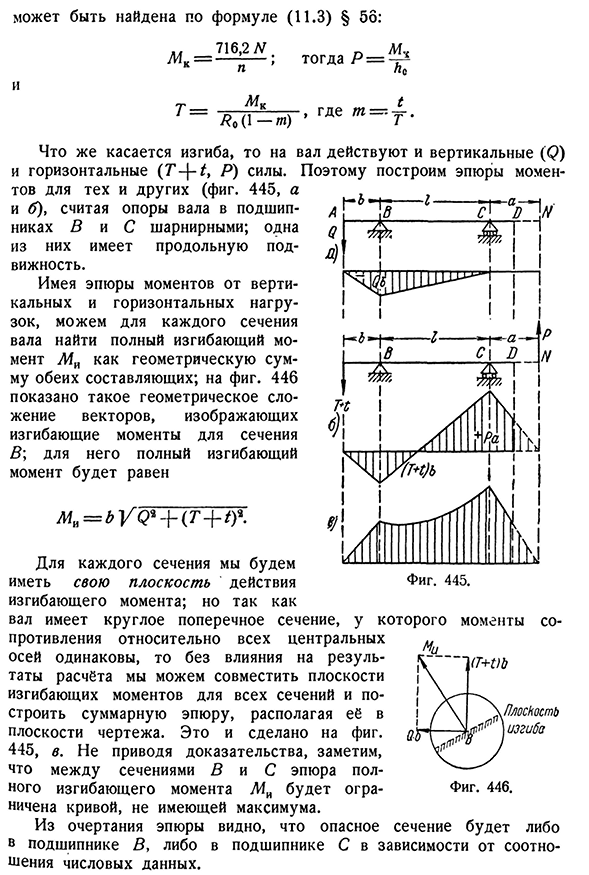
- R o приложены к концам вала; при равновесии, равномерном ходе машины, моменты этих пар равны и момент скручивания. Если мощность, передаваемая валом со скоростью вращения p и шкивом N в единицу времени, известна, то величина крутящего момента§ 166] определения изгиба и крутящего момента 511. Можно найти по формуле (11.3)§ 56: L4C= 716,2 Вт Тогда R= ХК И Т= 7?О (1-м)’ Где W=u. Что касается изгиба, то на вал действуют как вертикальные (Q), так
и горизонтальные (P) силы. Поэтому мы строим моменты appspy для каждого из них(рис. 445, а и в), считая подшипники В и с, опоры вала шарнирно сочленены; один из них имеет продольную подвижность. Имея график момента от вертикальной и горизонтальной нагрузок, мы показываем суммарный изгиб Mo 446 как геометрическую сумму обеих составляющих каждой секции вала, изображающую вектор-подобный геометрический изгибающий момент для секции\, где суммирующий момент равен Ma=V = V = V = V = V = V = V.
Фигура. Четыреста сорок пять Вал имеет круглое поперечное сечение, коэффициенты которого для его центральной оси одинаковы, Людмила Фирмаль
не влияя на результаты расчета, и мы изгибаем МО для всех сечений это делается на рисунке. 445, B. заметим, что график всего изгибающего момента L4I между участками B и C ограничен максимальной кривой, не давая доказательства Из контура графика видно, что опасной деталью может быть либо подшипник в, либо подшипник с, в зависимости от соотношения числовых данных.
Читайте также: Как посчитать дисторсию для вала
Видео:Понимание напряжений в балкахСкачать

ПроСопромат.ру
Видео:КРУЧЕНИЕ ВАЛА. Касательные напряжения. Сопромат.Скачать

Технический портал, посвященный Сопромату и истории его создания
Видео:БАЛКА - 90 СТУДЕНТОВ САМОСТОЯТЕЛЬНО СТРОЯТ ЭПЮРЫ после просмотра этого видео!Скачать

Расчет вала при совместном действии изгиба и кручения. Подбор сечения вала
Задача. Шкив с диаметром Д1 и с углом наклона ветвей ремня к горизонту 

1) определить моменты, приложенные к шкивам ;
2) построить эпюру крутящих моментов Мк ;
3) определить окружные усилия t1 и t2 ;
4) определить давления на вал, принимая их равными трем окружным усилиям ;
5) определить силы, изгибающие вал в горизонтальной и вертикальной плоскостях;
6) построить эпюры от горизонтальных сил Мг и от вертикальных сил Мв ;
7) построить эпюру суммарных изгибающих моментов;
8) найти опасное сечение и определить максимальный расчетный момент (по третьей теории прочности);
9) Подобрать диаметр вала d при [σ] =80MПа и округлить его значение.
1) Определяем крутящие моменты и строим эпюру крутящих моментов Т к
Соответствующие этим крутящим моментам окружные усилия t1 и t2 :
Усилие на шкиве Д1
Усилие на шкиве Д2
Тогда приведенное к центру вала давление на вал в местах насадки шкивов будет равно (по заданию принимая их равными трем окружным усилиям):
Определяем опорные реакции.
Расчетную схему представим в виде балки на двух опорах — шарнирно-неподвижной и шарнирно-подвижной.
Горизонтальная плоскость:
Вертикальная плоскость:
Строим эпюры изгибающих моментов от сил, действующих в горизонтальной и вертикальной плоскостях Мг и МB .
Определяем суммарные моменты по формуле :
Строим эпюру суммарных моментов М с .
Максимальный расчетный момент по третьей теории прочности:
Определим опасное сечение — оно будет в сечении, где максимален изгибающий и крутящий моменты (см. эпюры крутящих и суммарных изгибающих моментов). Для этого сечения и вычислим расчетный момент:
Читайте также: Отклонения формы поверхности вала для подшипника
Момент сопротивления сечения из найдем из формулы для изгиба , тогда:
где W – момент сопротивления при изгибе, W=0,1d 3
Видео:Определение реакций опор в балке. Сопромат.Скачать

Расчет валов
Критерии работоспособности и виды разрушений валов и осей
Для валов и осей применяют качественные углеродистые и легированные стали. Для валов и осей неответственных передач применяют стали обыкновенного качества (без термообработки).
Валы и оси обрабатывают на токарных станках, посадочные поверхности могут шлифоваться.
Валы и вращающиеся оси при работе испытывают циклически изменяющиеся напряжения (рис. 11.3) и чаще всего выходят из строя в результате усталостных разрушений.
Основными расчетными нагрузками являются крутящий момент (для валов) и изгибающий момент.
Основными критериями работоспособности являются прочность и жесткость.
Расчет валов проводится в два этапа: проектировочный только под действием крутящего момента и проверочный расчет с учетом крутящего и изгибающего моментов.
1. Проектировочный (предварительный) расчет вала проводят по формуле
где Мк — крутящий момент, Мк= Т; Т — вращающий момент на валу; d — диаметр вала; [тк] — допускаемое напряжение при кручении, [тк] = 20. 30 МПа.
Полученное значение диаметра вала округляют до ближайшего большего размера из ряда чисел R40 по ГОСТ «Нормальные линейные размеры» (см. табл. П37 Приложения). Форму и размеры вала уточняют при эскизной проработке вала после определения размеров колес, муфт и подшипников, по которым определяют длину шеек и цапф вала.
Проверочный расчет спроектированного вала проводят по сопротивлению усталости и на жесткость.
Предварительно определяют все конструктивные элементы вала, обработку и качество поверхности отдельных участков. Составляется расчетная схема вала и наносятся действующие нагрузки.
2. Проверочный уточненный расчет на сопротивление усталости заключается в определении расчетных коэффициентов запаса прочности в опасных сечениях, выявленных по эпюрам моментов с учетом концентрации напряжений.
Читайте также: Как открутить шкив коленчатого вала ваз 2110
Принимают, что напряжение изгиба меняется по симметричному циклу (см. рис. 11.3, а), а напряжение кручения — по отнулевому (см. рис. 11.3, б).
Амплитуда цикла изменения напряжений изгиба вала
где Мж — изгибающий момент;
амплитуда отнулевого цикла изменения напряжений кручения
где Wос, Wp — момент сопротивления изгибу и кручению сечений вала соответственно.
по нормальным напряжениям
по касательным напряжениям
где σ-1 — предел выносливости при расчете на изгиб; τ-1 — предел выносливости при расчете на кручение; KσD, KτD — общий коэффициент концентрации напряжений при изгибе и кручении соответственно:
где Кσ, Кτ, — коэффициенты снижения предела выносливости за счет местных концентраторов — галтелей, выточек, поперечных отверстий, шпоночных пазов (эффективный коэффициент концентрации напряжений); Kd — коэффициент влияния абсолютных размеров; KF — коэффициент влияния обработки поверхности; Kv — коэффициент упрочнения поверхности; значения перечисленных коэффициентов приведены в специальной литературе.
Расчетный коэффициент запаса выносливости в сечении при совместном действии изгиба и кручения
Минимально допустимое значение коэффициента запаса прочности 1,6. 2,5.
Расчет осей ведут только на изгиб: при расчете неподвижных осей принимают изменения напряжений по отнулевому циклу, при расчете подвижных — по симметричному.
3. Упрощенный проверочный расчет на усталость проводят в предположении, что нормальные напряжения (изгиба) и касательные напряжения (кручения) меняются по симметричному циклу. Одновременное действие крутящего и изгибающего моментов рассчитывается по гипотезе наибольших касательных напряжений
где Мп — суммарный изгибающий момент, геометрическая сумма изгибающих моментов в вертикальной и горизонтальной плоскостях:
Условие сопротивления усталости
где σэкв — эквивалентные напряжения в сечении; Мэкв — эквивалентный момент в сечении; d — диаметр вала в сечении; [σ-1и] — допускаемое напряжение изгиба при симметричном цикле изменения напряжений.
В большинстве случаев ограничиваются упрощенным проверочным расчетом. В специальных случаях используют коленчатые (непрямые) валы и валы с изменяемой формой геометрической оси (гибкие). Используют сплошные и полые (с осевым отверстием) валы.
- Свежие записи
- Чем отличается двухтактный мотор от четырехтактного
- Сколько масла заливать в редуктор мотоблока
- Какие моторы бывают у стиральных машин
- Какие валы отсутствуют в двухвальной кпп
- Как снять стопорную шайбу с вала
📸 Видео
Расчет вала на прочность и жесткость. Эпюра крутящих моментовСкачать
Расчет вала на изгиб с кручениемСкачать
Изгиб с кручениемСкачать
9.1 Расчет валов приводаСкачать
Определение экстремума эпюры моментов MСкачать
ЗАПОМНИ ТРИ ГЛАВНЫХ ПРАВИЛА и ты сможешь удивить своего препода по сопромату!Скачать
Продольная сила N, Поперечная сила Q, изгибающий момент М – ВИДНО? ДА, ВИДНО! ЗНАКИ ВИДНО? ВИДНО!Скачать
Кручение. Расчет составного вала кольцевого сечения.Скачать
Прочность и жесткость валов. Часть 6: Эпюры моментов выходного вала (цилиндрическая передача).Скачать
Как построить эпюры изгибающего момента и поперечной силы. СопроматСкачать
Изгиб с кручением пример решения задач по сопротивлению материаловСкачать
Изгиб с кручением пример решения задач по сопротивлению материалов. Теории прочностиСкачать
Кручение зажатого валаСкачать
Кручение валаСкачать
ОРИГИНАЛЬНЫЙ МЕТОД ОБУЧЕНИЯ СОПРОМАТУ. Проверка прочности сечения.Скачать