Формула расчета передаточного числа в планетарном редукторе

Планетарными называют передачи, имеющие зубчатые колеса с подвижными осями. Отличительной особенностью механизмов, включающих планетарную передачу (или передачи), является наличие двух или более степеней свободы. При этом угловая скорость любого звена передачи определяется угловыми скоростями остальных звеньев.

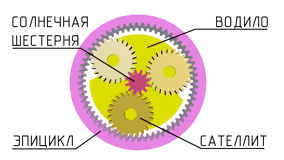
Наибольшее распространение получила простая одинарная планетарная передача (рис. 1), которая состоит из центрального колеса 1 с наружными зубьями, неподвижного центрального колеса 3 с внутренними зубьями; сателлитов 2 – колес с наружными зубьями, зацепляющихся одновременно с колесами 1 и 3 (на рис. 1 число сателлитов с = 3), и водила Н, на котором закреплены оси сателлитов. Водило соединено с тихоходным валом. В планетарной передаче одно колесо неподвижно (соединено с корпусом). Обычно внешнее центральное колесо с внутренними зубьями называют коронным (коронная шестерня или эпицикл), а внутреннее колесо с внешними зубьями – солнечным колесом (солнечная шестерня или солнце).

При неподвижном колесе 3 вращение колеса 1 вызывает вращение сателлитов 2 относительно собственных осей, а обкатывание сателлитов по колесу 3 перемещает их оси и вращает водило Н. Сателлиты таким образом совершают вращение относительно водила и вместе с водилом вокруг центральной оси, с. е. совершают движение, подобное движению планет. Поэтому такие передачи и называют планетарными.

При неподвижном колесе 3 движение передают чаще всего от колеса 1 к водилу Н, можно передавать движение от водила Н к колесу 1.

В планетарных передачах применяют не только цилиндрические, но и конические колеса с прямым или косым зубом.

Если в планетарной передаче сделать подвижными все звенья, т. е. оба колеса и водило, то такую передачу называют дифференциальной .
С помощью дифференциального механизма можно суммировать движение двух звеньев на одном или раскладывать движение одного звена на два других. Например, в дифференциале заднего моста автомобиля движение от водила Н передают одновременно колесам 1 и 3, что позволяет при повороте одному колесу вращаться быстрее другого.

Разновидности планетарных передач

Существует много различных типов и конструкций планетарных передач. Наиболее широко в машиностроении применяют однорядную планетарную передачу, схема которой показана на рисунке 1. Эта передача конструктивно проста, имеет малые габариты. Находит применение в силовых и вспомогательных приводах. КПД планетарной передачи η = 0,96…0,98 при передаточных числах u = 3…8.

Планетарные механизмы, в составе которых присутствуют одна или несколько планетарных передач подразделяются на однорядные, двухрядные и многорядные. Каждый набор из центральных зубчатых колёс и сателлитов, вращающихся в одной плоскости, образует так называемый планетарный ряд . Простой планетарный механизм с набором одновенцовых сателлитов является однорядным. Простые планетарные механизмы с двухвенцовыми сателлитами являются двухрядными. Сложные планетарные механизмы могут быть двух, трёх, четырёх и даже пятирядными.

Для получения больших передаточных чисел в силовых приводах применяют многоступенчатые планетарные передачи. На рис. 2,а планетарная передача составлена из двух последовательно соединенных однорядных планетарных передач. В этом случае суммарное передаточное число u = u₁×u₂ ≤ 64, а КПД равен η = η₁×η₂ = 0,92…0,96.

На рисунке 2, б показана схема планетарной передачи с двухрядным (двухвенцовым) сателлитом, для которой при передаче движения от колеса 1 к водилу Н при n₄ = 0 передаточное число определяется из зависимостей:

В этой передаче u = 3…19 при КПД η = 0,95…0,97.

Как упоминалось выше, планетарные передачи, у которых все звенья подвижны, называют дифференциальными или просто дифференциалами.

Неизбежные погрешности изготовления приводят к неравномерному распределению нагрузки между сателлитами. Для выравнивания нагрузки в передачах с тремя сателлитами одно из центральных колес выполняют самоустанавливающимся в радиальном направлении (не имеющим радиальных опор). Для самоустановки сателлитов по неподвижному центральному колесу применяют сферические подшипники качения.
Высокие требования предъявляются к прочности и жесткости водила, при этом его масса должна быть минимальной. Обычно водила выполняют литыми или сварными.

Достоинства и недостатки планетарных передач

Основными достоинствами планетарных передач являются:

• малые габариты и масса вследствие передачи мощности по нескольким потокам, численно равным количеству сателлитов. При этом нагрузка в каждом зацеплении уменьшается в несколько раз;
• удобство компоновки в машинах благодаря соосности ведущего и ведомого валов;
• работа с меньшим шумом, чем в обычных зубчатых передачах, что обусловлено меньшими размерами колес и замыканием сил в механизме. При симметричном расположении сателлитов силы в передаче взаимно уравновешиваются;
• малые нагрузки на валы и опоры, что упрощает конструкцию опор и снижает потери в них;
• возможность получения больших передаточных чисел при небольшом числе зубчатых колес и малых габаритах передачи.

Не лишены планетарные передачи и недостатков:

• повышенные требования к точности изготовления и монтажа передачи;
• большее количество деталей, в т. ч. подшипников, и более сложная сборка.

Область применения планетарных передач

Планетарные передачи применяют как редукторы в силовых передачах и приборах, в коробках передач автомобилей и другой самоходной техники, при этом передаточное число такой КПП может изменяться путем поочередного торможения различных звеньев (например, водила или одного из колес), в дифференциалах автомобилей, тракторов и т. п.

Читайте также: Ремонт редуктора заднего моста мерседес спринтер 906

Широкое применение планетарные передачи нашли в автоматических коробках передач автомобилей благодаря удобству управления передаточными числами (переключением передач) и компактности. Можно встретить планетарные передачи и в механизмах привода ведущих колес современных велосипедов. Часто применяют планетарную передачу, совмещенную с электродвигателем (мотор-редуктор, мотор-колесо).

Передаточное число планетарных передач

При определение передаточного числа планетарной передачи используют метод остановки водила ( метод Виллиса ).
По этому методу всей планетарной передаче мысленно сообщается дополнительное вращение с частотой вращения водила n_Н , но в обратном направлении. При этом водило как бы останавливается, а закрепленное колесо освобождается. Получается так называемый обращенный механизм, представляющий собой обычную непланетарную передачу, в которой геометрические оси всех колес неподвижны. Сателлиты при этом становятся промежуточными (паразитными) колесами, т. е. колесами, не влияющими на передаточное число всего механизма.
Передаточное число в обращенном механизме определяется как в духступенчатой передаче с одним внешним и вторым внутренним зацеплением.

Здесь существенное значение имеет знак передаточного числа. Передаточное число считают положительным, если в обращенном механизме ведущее и ведомое звенья вращаются в одну сторону, и отрицательным, если в разные стороны. Так, для обращенного механизма передачи по рис. 1 имеем:

где z – числа зубьев колес.

В рассматриваемом обращенном механизме знак минус показывает, что колеса 2 и 3 вращаются в обратную сторону по отношению к колесу 1.

В качестве примера определим передаточное число для планетарной передачи, изображенной на рис. 1, при передаче движения от колеса 1 к водилу Н. Мысленная остановка водила в этой передаче равноценна вычитанию его частоты n_Н из частоты вращения колес.
Тогда для обращенного механизма этой передачи имеем:

Для планетарной передачи, у которой колесо 3 закреплено в корпусе неподвижно ( n₃ = 0), колесо 1 является ведущим, а водило Н – ведомым.
Тогда получим передаточное число такой передачи:

Подбор чисел зубьев планетарных передач

В отличие от обычных зубчатых передач расчет планетарных начинают с подбора чисел зубьев на колесах и сателлитах. Рассмотрим последовательность подбора чисел зубьев на примере планетарной передачи, изображенной на рис. 1.

Число зубьев z₁ центральной шестерни 1 задают из условия неподрезания ножки зуба: z₁ ≥ 17. Принимают z₁ = 24 при Н ≤ 350 НВ; z₁ = 21 при Н ≤ 52 HRC и z₁ = 17 при Н > 52 HRC.

Число зубьев неподвижного центрального колеса 3 определяют по заданному передаточному числу u :

Число зубьев z₂ сателлита 2 вычисляют из условия соосности, в соответствии которым межосевые расстояния a_w зубчатых пар с внешним и внутренним зацеплением должны быть равны.
Из рис. 1 для немодифицированной прямозубой передачи:

где d = mz — делительные диаметры колес.

Так как модули зацеплений планетарной передачи одинаковые, то формула (1) принимает вид:

Полученные числа зубьев z₁ , z₂ , и z₃ проверяют по условиям сборки и соседства.

Условие сборки требует, чтобы во всех зацеплениях центральных колес с сателлитами имело место совпадение зубьев со впадинами, в противном случае собрать передачу будет невозможно. Установлено, что при симметричном расположении сателлитов условие сборки удовлетворяется, когда сумма зубьев центральных колес (z₁ + z₃) кратна числу сателлитов с = 2…6 (обычно с = 3), т. е. должно соблюдаться условие:

Условие соседства требует, чтобы сателлиты не задевали зубьями друг друга. Для этого необходимо, чтобы сумма радиусов вершин зубьев соседних сателлитов, равная d_a2 = m(z₂ + 2 ) , была меньше расстояния l между их осями (рис. 1), т. е.:

Из формулы (2) следует, что условие соседства удовлетворяется, когда

Расчет на прочность планетарных передач

Расчет на прочность зубчатых передач планетарного типа ведут по методике, применяемой для обычных зубчатых передач. Основными критериями работоспособности для большинства планетарных передач (как и для всех зубчатых передач), является усталостная контактная прочность рабочих поверхностей зубьев и прочность зубьев при изгибе. При этом под контактной прочностью понимают способность контактирующих поверхностей зубьев обеспечить требуемую безопасность против прогрессирующего усталостного выкрашивания, а прочностью при изгибе – способность зубьев обеспечить требуемую безопасность против усталостного излома зуба.

Расчет выполняют для каждого зацепления. Например, в передаче, изображенной на рис. 1, необходимо рассчитать внешнее зацепление колес 1 и 2 и внутреннее – колес 2 и 3. Так как модули и силы в этих зацеплениях одинаковы, а внутреннее зацепление по своим свойствам прочнее внешнего, то при одинаковых материалах колес достаточно рассчитать только внешнее зацепление.

Расчет начинают с подбора чисел зубьев колес, как было показано выше.

При определении допускаемых напряжений коэффициенты долговечности находят по эквивалентных числам циклов нагружения. При этом число циклов перемены напряжений зубьев за весь срок службы вычисляют при вращении колес только относительно друг друга.

Читайте также: Задний редуктор ford escape

При определении допускаемых напряжений изгиба для зубьев сателлита вводят коэффициент Y_A , учитывающий двустороннее приложение нагрузки (симметричный цикл нагружения).

Межосевое расстояние планетарной прямозубой передачи для пары колес внешнего зацепления (центральной шестерни с сателлитом) определяют по формуле:

где u’ = z₂/z₁ – передаточное число рассчитываемой пары колес;
К_c = 1,05…1,15 – коэффициент неравномерности распределения нагрузки между сателлитами;
Т₁ – вращающий момент на валу центральной шестерни, Нм;
с – число сателлитов;
ψ_ba — коэффициент ширины венца колеса:
ψ_ba = 0,4 для Н ≤ 350 НВ;
ψ_ba = 0,315 при 350 НВ ψ_ba = 0,25 для Н > 50 HRC.

Ширина b₃ центрального колеса 3 определяется по формуле b₃ = ψ_baa_w .
Ширину b₂ венца сателлита принимают на 2…4 мм больше значения b₃ ; ширина центральной шестерни b₁ = 1,1 b₂ .

Модуль зацепления определяют по формуле:

Получнный расчетом модуль округляют до ближайшего стандартного значения, а затем уточняют межосевое расстояние:

Окружную силу F_t в зацеплении вычисляют по формуле:

Радиальную силу F_r определяют по формуле:

где α_w = 20˚ – угол зацепления.

Видео:Расчет планетарной зубчатой передачиСкачать

Расчет передаточного числа планетарного редуктора

Планетарные редукторы относятся к механическим зубчатым передачам.

Механические передачи служат для передачи энергии на расстояние, как правило с преобразованием по скорости и моменту. В зубчатых передачах движение осуществляется благодаря непосредственному контакту зубчатых коле

Редуктор – это устройство преобразующее высокую угловую скорость вращения входного вала (от двигателя) в более низкую на выходном валу (к полезной нагрузке), повышая при этом вращающий момент.

Передаточное отношение (i) – это отношение угловой скорости ведущего вала к угловой скорости ведомого вала .

Планетарные редукторы – это механизмы в которых оси отдельных колес являются подвижными. Простейший планетарный редуктор, состоящий из четырех звеньев, изображен на рисунке 1. В этих редукторах колеса с подвижными осями вращения называются планетарными колесами или сателлитами (звено 1), а звено, на котором располагаются оси сателлитов, – водилом или планетарным водилом [H] (звено 2). Зубчатые колеса с неподвижными осями вращения называются солнечными или центральными (звено 3); неподвижное колесо – коронной шестерней, эпициклом или опорным колесом (звено 4). На практике, для повышения прочности планетарного редуктора, количество сателлитов увеличивают до максимально возможного. Планетарный редуктор, изображенный на рисунке 1, носит название редуктора Джемса.

Рис. 1. Простейший планетарный редуктор.

Передаточное отношение U от колеса 3 до водила H редуктора, при неподвижной коронной шестерне, имеет вид:

где, U – коэффициент передаточного отношения;
индекс (1) – указывает на что, что неподвижным является элемент 1, в данном случае это коронная шестерня;
индексы 3 и H – указывают, что расчет передаточного отношения от колеса 3 (солнечная шестерня) к водилу H;
r – радиусы колес, индексы указывают на радиус соответствующего колеса (r1 – радиус коронной шестерни);
z – количество зубьев шестерни, индексы указывают на количество зубьев соответствующего колеса);

На рисунке 2 изображен вид классического одноступенчатого планетарного редуктора:

Рис. 2 Одноступенчатый планетарный редуктор

При использовании планетарной передачи в качестве редуктора один из трёх её основных элементов фиксируется неподвижно, а два других служат в качестве ведущего и ведомого. Таким образом, передаточное отношение будет зависеть от количества зубьев каждого компонента, а также от того, какой элемент закреплён. Для получения самого большого передаточного отношения, неподвижным оставляют коронную шестерню, см. рисунок 3. Такие передачи как правило используют в планетарных мотор-редукторах, на транспорте и машиностроении.

Рис. 3. Анимация работы одноступенчатого планетарного редуктора, с неподвижным эпициклом

На практике широко применяются многоступенчатые планетарные редукторы. Давайте рассмотрим двигатель постоянного тока с планетарным редуктором. Для примера возьмем планетарный мотор-редуктор МРП42 производства ООО «Электропривод» с передаточным отношением 1/144. Такое большое передаточное отношение можно получить, используя редуктор с несколькими ступенями. На рисунке 4 изображена первая ступень.

Рис. 4. Первая ступень планетарного редуктора.

Вращение от мотора передается на водило через сателлиты первой ступени. На водиле первой ступени закреплена шестеренка передающая вращение дальше (на вторую ступень).

Передаточное отношение первого звена:

Вторая ступень, мало отличается от первой, см. рисунок 5.

Рис. 5. Вторая ступень планетарного редуктора

Передаточное отношение второго звена:

В третьей ступени установлены четыре сателлита, для увеличения нагрузочной способности на редуктор, вследствие чего уменьшен их диаметр, рисунок 6.

Передаточное отношение второго звена:

Рис. 6. Третья ступень планетарного редуктора.

Подсчет полного передаточного отношения, складывается из произведения передаточных отношений все звеньев, вошедших в состав редуктора:

Подсчитанное по формулам передаточное отношение соответствует заявленному для рассматриваемого в нашем примере мотор-редуктора.

Законченный вариант планетарного редуктора изображен на рисунке 7, в нем добавлен присоединительный фланец с установленным подшипником скольжения. В этом редукторе все шестерни выполнены из металла, что обуславливает продолжительный жизненный цикл изделия.

Читайте также: Из чего прокладка крышки редуктора

Рис. 7. Планетарный редуктор в сборе.

Приглашаем на выставку «МЕТАЛЛООБРАБОТКА-2018»

Приглашаем на выставку «Росупак-2017»

Приглашаем на выставку «Металлообработка-2017»

В продаже мотор-редукторы МРП, МРЦ

BMD-R – блоки дистанционного управления коллекторными двигателями постоянного тока

BMD-DIN – начат выпуск блоков управления коллекторными двигателями с креплением на DIN-рейку

Загрузить всю книгу

Видео:Планетарная передача пять передаточных чисел в однойСкачать

2.3. Передаточное отношение планетарных и дифференциальных механизмов

Звенья, вращающиеся вокруг неподвижной оси, называются основными или центральными.

Центральное колесо 1 называется солнечным, а неподвижное 3 – коронным или корончатым. Зубчатое колесо 2 имеющее подвижную ось называется сателлитом. Звено Н называется водилом или поводком. Механизмы, в состав которых входят зубчатые колеса с подвижными осями называются планетарными или дифференциальными.

Планетарными (рис. 14 а) называются механизмы, имеющие одну степень свободы. Дифференциальные (рис. 14 б) механизмы имеют две и более степени свободы.

Эти механизмы обязательно должны быть соосными, то есть оси солнечных колёс должны располагаться на одной и той же прямой линии.

Рассмотрим дифференциальный механизм (рис. 15).

, таким образом определённость в движении звеньев этого механизма будет в том случае, если будут известны законы движения двух его ведущих звеньев.

Так как сателлиты имеют подвижные оси, то использовать формулы для расчёта передаточного отношения механизмов с неподвижными осями не представляется возможным. В этом случае прибегают к методу инверсии (метод обращённого движения).

Будем рассматривать движение всех колёс относительно водила. Всем звеньям зададим вращательное движение с угловой скоростью водила, но в обратном направлении и найдём скорости всех звеньев механизма. Для этого вычтем угловую скорость водила из всех угловых скоростей колёс.

Скорость звена в действительном движении (до инверсии)

Скорость звена в обращённом движении (после инверсии)

Механизм, полученный в результате инверсии (остановки водила) называется обращённым (рис. 16). В результате получили обычную зубчатую передачу с неподвижными осями.

Эту зависимость (1) называют формулой Виллиса для дифференциальных механизмов.

Дифференциальный механизм никакого определённого передаточного отношения не имеет, если ведущим является одно из звеньев (колесо или водило), и приобретает определённость, если ведущих колёс будет два.

Передаточное отношение обращённого механизма можно рассчитать,

У планетарных механизмов (рис. 2.29) одно из центральных (основных) колёс неподвижно, тогда формула Виллиса примет вид:

или в общем случае:

Передаточное отношение планетарного механизма от любого n-го колеса равно 1 минус передаточное отношение от этого же самого колеса к солнечному колесу, при неподвижном водиле.

Планетарными называют передачи , в которых , кроме зубчатых ко – лес с неподвижными осями , имеются колеса , вращающиеся и одновре – менно перемещающиеся по окружности ( планетарные колеса или сател – литы ).

Планетарные передачи отличаются компактностью при больших передаточных числах . Вес планетарного редуктора в 2 – 3 раза меньше

по сравнению с весом простых зубчатых редукторов тех же мощностей и передаточных чисел . Это достигается за счет распределения нагрузки между несколькими сателлитами и применения внутреннего зацепле – ния . Однако планетарные передачи требуют повышенной точности из – готовления и сложнее в сборке , чем простые . На практике встречается большое количество различных схем планетарных механизмов [1], в данном разделе рассмотрим наиболее известные из них ( рис .1).

Рис .1. Схемы планетарных передач : а – с одновенцовым сателлитом ; б – с двух – венцовым сателлитом , с одним внешним и одним внутренним зацеплением ; в – с двухвенцовым сателлитом , с двумя внешними зацеплениями ; г – с двухвен – цовым сателлитом , с двумя внутренними зацеплениями . 1, 3 – центральные зуб – чатые колеса ; 2, 2′ – планетарные колеса или сателлиты ; H – водило

Звено , в котором закреплены оси сателлитов , называют водилом H .

В одних схемах движение подается на одно из центральных колес ,

а снимается с водила , в других ведущим является водило , а ведомым – центральное колесо .

PDF created with FinePrint pdfFactory Pro trial version http://www.fineprint.com

Видео:Как узнать передаточное число редуктора?Скачать

Передаточное отношение планетарной передачи

При определении передаточного отношения планетарного меха – низма используют метод обращения движения . Он состоит в том , что всем звеньям механизма сообщают добавочную угловую скорость , рав –

ную по величине угловой скорости водила и противоположную ей по направлению (– w Н ). Тогда угловые скорости всех колес уменьшаются на величину w Н , а угловая скорость водила становится равной нулю , и пла – нетарный редуктор превращается в простой зубчатый , для которого от –

ношение угловых скоростей может быть выражено через отношение

чисел зубьев входящих в него колес .

Формула передаточного отношения планетарных механизмов для приведенных на рис .1 схем имеет вид :

• Свежие записи
  • Чем отличается двухтактный мотор от четырехтактного
  • Сколько масла заливать в редуктор мотоблока
  • Какие моторы бывают у стиральных машин
  • Какие валы отсутствуют в двухвальной кпп
  • Как снять стопорную шайбу с вала

  
  

  источники:

  https://evakuatorinfo.ru/formula-rascheta-peredatochnogo-chisla-v-planetarnom-reduktore

  📽️ Видео

  Передаточное число шестерен. Паразитные шестерниСкачать

  

  Как вычислить передаточное число редуктораСкачать

  

  5 режимов работы планетарной передачи дифференциального механизмаСкачать

  

  Как рассчитать передаточное число (отношение) зубчатого редуктораСкачать

  

  Кратко о передаточном числе в зубчатой передаче.Скачать

  

  Двухрядный планетарный редуктор 1:36 / Double Row Planetary Gearbox 1:36Скачать

  

  Загадочная планетарная передача [Ликбез для всех]Скачать

  

  7. Определение передаточного отношения планетарного механизма аналитическим методомСкачать

  

  Легко! Узнать передаточное число редуктора, без вскрытия!!Скачать

  

  7 недостатков планетарной передачиСкачать

  

  7 преимуществ планетарной передачи для инженера конструктораСкачать

  

  Как считать передаточные числа трансмиссии, скорость и тягу автомобиляСкачать

  

  Передаточное число или отношениеСкачать

  

  Как планетарный механизм дает больше крутящего момента при одних и тех же размерахСкачать

  

  Инверсный планетарный редуктор, прецессирующий редуктор - объяснение большого передаточного числаСкачать

  

  Кинематика планетарного механизмаСкачать

  

  4. Определение передаточного отношения планетарного механизма графическим методомСкачать