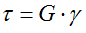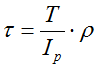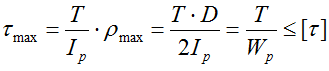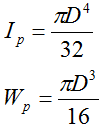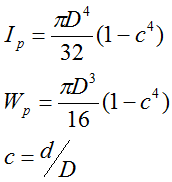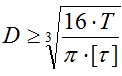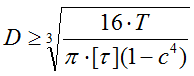Формулу для расчета угла закручивания вала

На этой странице приведен еще один пример решения задачи по Сопромату, в которой необходимо произвести расчет вала переменного сечения (ступенчатого), нагруженного крутящими моментами. По результатам расчетов необходимо подобрать размеры вала, а также определить максимальную деформацию вала на скручивание (угол закручивания).

Результаты расчетов оформлены эпюрами крутящих моментов, касательных напряжений и углов закручивания бруса.

Студентам технических специальностей ВУЗов в качестве методической помощи предлагаются к скачиванию готовые варианты контрольных работ по сопромату (прикладной механике). Представленные задания и примеры их решения предназначены, в частности, для учащихся Алтайского Государственного технического университета.
Варианты контрольных работ можно скачать в формате Word для ознакомления с порядком решения заданий, или для распечатывания и защиты (при совпадении вариантов).

Видео:КРУЧЕНИЕ ВАЛА. Касательные напряжения. Сопромат.Скачать

Расчет вала

Условие задачи:

К стальному валу, состоящему из 4-х участков длиной l₁…l₄ приложено четыре сосредоточенных момента М₁…М₄ (см. рис. 1 ).

Требуется:

Построить эпюру крутящих моментов М_кр , подобрать диаметр вала из расчета на прочность, построить эпюру максимальных касательных напряжений τ_max , построить эпюру углов закручивания φ вала и определить наибольший относительный угол закручивания вала.

Исходные данные:

Указания:

Вычертить схему вала в соответствии с исходными данными.
Знаки моментов в исходных данных означают: плюс – момент действует против часовой стрелки относительно оси Z , минус – по часовой стрелке (см. навстречу оси Z ). В дальнейшем значения моментов принимать по абсолютной величине.
Участки нумеровать от опоры.
Допускаемое касательное напряжение [ τ ] для стали принимать равным 100 МПа.

Решение:

1. Определим методом сечений значения крутящих моментов на каждом силовом участке от свободного конца вала.
Крутящий момент равен алгебраической сумме внешних моментов, действующих на вал по одну сторону сечения.

2. Подберем сечение вала из расчета на прочность при кручении по полярному моменту сопротивления для участка, где величина крутящего момента максимальная (без учета знака):

Так как для круглого сечения полярный момент равен: W_р = πD 3 /16 , то можно записать:

D ≥ 3 √ (16М_кр/π[τ]) ≥ 3√(16×12,2×10 3 /3,14×[100×10 6 ]) = 0,0855 м или D ≥ 85,5 мм.

( Здесь и далее знак «√» означает квадратный корень из выражения )

В соответствии со стандартным рядом, предусмотренным ГОСТ 12080-66, принимаем диаметр вала D = 90 мм.

3. Определим угол закручивания для каждого участка вала по формуле:

где
G – модуль упругости 2-го рода; для стали G = 8×10 10 Па;
I_p – полярный момент инерции (для круглого сечения I_р = πD 4 /32 ≈ 0,1D 4 , м 4 ).
Произведение G×I_р = 8×10 10 ×0,1×0,094 ≈ 524880 Н×м 2 – жесткость сечения данного вала при кручении.

Расчитываем углы закручивания на каждом участке:

4. Определяем углы закручивания сечений вала, начиная от жесткой заделки (опоры):

5. Определяем максимальное касательное напряжение на каждом силовом участке по формуле:

6. Наибольший относительный угол закручивания Θ_max определим по формуле:

7. По результатам расчетов строим эпюры крутящих моментов М_кр , касательных напряжений τ_max и углов закручивания φ (см. рис. 2).

Читайте также: Хонда элемент датчик входного вала

Видео:Кручение. Расчет составного вала кольцевого сечения.Скачать

Расчеты стержней при кручении

Нагружение стержня, при котором из всех внутренних силовых факторов в его поперечных сечениях не равен нулю только момент, вектор которого направлен вдоль оси стержня, называется кручением. Стержни, работающие в таких условиях, называются валами.

При кручении цилиндрического вала, в его поперечных сечениях возникают только касательные напряжения, и это напряженное состояние называется «чистый сдвиг». При этом, поперечные сечения вала остаются плоскими и не меняют своего размера в радиальном направлении. Так же не меняются расстояния между поперечными сечениями, но при этом они поворачиваются друг относительно друга на некоторый угол φ.

В общем случае, максимальные касательные напряжения возникают у края поперечного сечения, за исключением наружных углов, в которых касательные напряжения равны нулю. Стержень не круглого поперечного сечения испытывает депланации — точки его сечения выходят из плоскости и перемещаются вдоль оси стержня в различных направлениях.

Онлайн расчеты, представленные в данном разделе, рассматривают кручение круглого вала сплошного сечения, кручение круглого вала с отверстием, выполненным с эксцентриситетом, треугольное, прямоугольное сечение, а так же кручение стержней стандартных сечений — уголка, двутавра и швеллера.

Видео:КРУЧЕНИЕ. ЭПЮРЫ ЗАКРУЧИВАНИЯ. Углы поворота. СопроматСкачать

Расчет кручения вала круглого сечения

Расчет максимальных касательных напряжений и угла поворота при кручении вала сплошного круглого сечения.

Исходные данные:

D — наружный диаметр вала, в миллиметрах;

L — длина вала, в миллиметрах;

Т — крутящий момент на валу, в ньютонах × метр;

Е — модуль упругости материала вала, в паскалях.

КРУЧЕНИЕ ВАЛА КРУГЛОГО СЕЧЕНИЯ

Крутящий момент на валу Т, Н*м

Максимальное касательное напряжение τ, МПа

Максимальное касательное напряжение:

Угол поворота:

φ = 2T×L / (π×r 4 × G),где
G — модуль сдвига.

Видео:Расчет вала на прочность и жесткость. Эпюра крутящих моментовСкачать

Расчет кручения вала круглого сечения с отверстием

Расчет максимальных касательных напряжений и угла поворота при кручении вала круглого сечения c отверстием.

Исходные данные:

D — наружный диаметр вала, в миллиметрах;

d — внутренний диаметр вала, в миллиметрах;

e — эксцентриситет отверстия, в миллиметрах;

L — длина вала, в миллиметрах;

Т — крутящий момент на валу, в ньютонах × метр;

Е — модуль упругости материала вала, в паскалях.

КРУЧЕНИЕ ВАЛА С ОТВЕРСТИЕМ

Крутящий момент на валу Т, Н*м

Максимальное касательное напряжение τ, МПа

Видео:Сопромат №4: Расчет вала на прочность и жесткостьСкачать

Расчет кручения стержня прямоугольного сечения

Расчет максимальных касательных напряжений и угла поворота при кручении стержня прямоугольного сечения.

Исходные данные:

a — длина сечения стержня, в миллиметрах;

b — высота сечения стержня, в миллиметрах;

L — длина стержня, в миллиметрах;

Т — крутящий момент, в ньютонах × метр;

Е — модуль упругости материала стержня, в паскалях.

КРУЧЕНИЕ ПРЯМОУГОЛЬНОГО СТЕРЖНЯ

Максимальное касательное напряжение τ, МПа

Видео:Сопротивление материалов. Лекция: кручение тонкостенного профиляСкачать

Расчет кручения стержня треугольного сечения

Расчет максимальных касательных напряжений и угла поворота при кручении стержня треугольного равнобедренного сечения.

Исходные данные:

a — длина основания сечения стержня, в миллиметрах;

b — длина боковой стороны сечения стержня, в миллиметрах;

L — длина стержня, в миллиметрах;

Т — крутящий момент, в ньютонах × метр;

Читайте также: Замена вала hp 1018

Е — модуль упругости материала стержня, в паскалях.

КРУЧЕНИЕ СТЕРЖНЯ ТРЕУГОЛЬНОГО СЕЧЕНИЯ

Длина боковой стороны b, мм

Максимальное касательное напряжение τ, МПа

Видео:Определение центра тяжести сложных сечений. Фигуры из ГОСТ.Скачать

Расчет кручения стержня прямоугольного сечения с тонкой стенкой

Расчет максимальных касательных напряжений (τ на стороне b иτ₁ на стороне a) и угла поворота при кручении стержня прямоугольного сечения с тонкой стенкой.

Исходные данные:

a — длина сечения сечения стержня, в миллиметрах;

b — высота сечения стержня, в миллиметрах;

s — толщина стенки стержня на стороне b, в миллиметрах;

s₁ — толщина стенки стержня на стороне a, в миллиметрах;

L — длина стержня, в миллиметрах;

Т — крутящий момент, в ньютонах × метр;

Е — модуль упругости материала стержня, в паскалях.

КРУЧЕНИЕ ТОНКОСТЕННОГО ПРЯМОУГОЛЬНОГО СТЕРЖНЯ

Максимальное касательное напряжение τ, МПа

Максимальное касательное напряжение τ₁, МПа

Видео:Кручение. Часть 6 Жесткость валаСкачать

Расчет кручения уголка

Расчет максимальных касательных напряжений и угла поворота при кручении уголка.
Стержни таких поперечных сечений как уголок, швеллер, двутавр никогда не предназначаются для передачи крутящего момента, но в некоторых случаях могут испытывать крутящие нагрузки вследствие особенностей общей геометрии конструкции.

Исходные данные:

a — высота уголка, в миллиметрах;

b — ширина уголка, в миллиметрах;

b, d — толщина полок уголка, в миллиметрах;

r — радиус закругления полок, в миллиметрах;

L — длина стержня, в миллиметрах;

Т — крутящий момент, в ньютонах × метр;

Е — модуль упругости материала стержня, в паскалях.

Максимальное касательное напряжение τ, МПа

Видео:9.1 Расчет валов приводаСкачать

Расчет кручения швеллера

Расчет максимальных касательных напряжений и угла поворота при кручении швеллера.

Исходные данные:

a — ширина швеллера, в миллиметрах;

с — высота швеллера, в миллиметрах;

b — толщина полки, в миллиметрах;

d — толщина стенки, в миллиметрах;

r — внутренний радиус закругления, в миллиметрах;

L — длина стержня, в миллиметрах;

Т — крутящий момент, в ньютонах × метр;

Е — модуль упругости материала стержня, в паскалях.

Максимальное касательное напряжение τ, МПа

Видео:Сопротивление материалов. Лекция: кручение круглого стержняСкачать

Расчет кручения двутавра

Расчет максимальных касательных напряжений и угла поворота при кручении двутавра.

Исходные данные:

a — ширина двутавра, в миллиметрах;

с — высота двутавра, в миллиметрах;

b — толщина полки, в миллиметрах;

d — толщина стенки, в миллиметрах;

r — внутренний радиус закругления, в миллиметрах;

L — длина стержня, в миллиметрах;

Т — крутящий момент, в ньютонах × метр;

Е — модуль упругости материала стержня, в паскалях.

Видео:11. Кручение ( практический курс по сопромату )Скачать

iSopromat.ru

Подборка формул для расчета валов и брусьев на кручение и решения задач сопротивления материалов по расчету внутренних моментов, касательных напряжений, деформаций и углов закручивания при кручении.

τ — касательные напряжения,
T – внутренний крутящий момент,
I_p – полярный момент инерции сечения вала,
W_p – полярный момент сопротивления сечения,
[ τ ] – допустимое напряжение,
G – модуль упругости II рода (модуль сдвига),
ρ — расстояние от центра сечения до рассматриваемой точки,
D – внешний диаметр вала,
d – внутренний диаметр вала кольцевого сечения.

Закон Гука при кручении (чистом сдвиге)

Расчет касательных напряжений в произвольной точке сечения вала

Формулы полярных моментов инерции и сопротивления

Читайте также: Шарнир карданного вала газ

• для вала сплошного (круглого) сечения
  
• для вала кольцевого сечения
  

Формулы для подбора диаметра вала по условию прочности

• сплошное круглое сечение
  
• кольцевое сечение
  

Абсолютные деформации (угол закручивания участков вала)

Видео:Кручение валаСкачать

Тема 2.4. Кручение

Под кручением понимается такой вид деформации, когда в поперечных сечениях бруса действует только крутящий момент M_k, (другое обозначение T, M_z), а остальные силовые факторы (нормальная и поперечная силы и изгибающие моменты) отсутствуют.

Или другое определение кручением называют деформацию, возникающую при действии на стержень пары сил, расположенной в плоскости, перпендикулярной к его оси (рис.1).

Кручение возникает в валах, винтовых пружинах, в элементах пространственных конструкций и т.п.

Деформация кручения наблюдается если прямой брус нагружен внешними моментами (парами сил M), плоскости действия которых перпендикулярны к его продольной оси

В чистом виде деформация кручения встречается редко, обычно присутствуют и другие внутренние силовые факторы (изгибающие моменты, продольные силы).

Стержни круглого или кольцевого сечения, работающие на кручение, называют валами.

Внешние крутящие моменты передаются на вал в местах посадки на него шкивов, зубчатых колес, там, где поперечная нагрузка смещена относительно оси вала.

Мы будем рассматривать прямой брус только в состоянии покоя или равномерного вращения. В этом случае алгебраическая сумма всех внешних скручивающих моментов, приложенных к брусу, будет равна нулю.

При расчете брусьев, испытывающий деформацию кручения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от M_k), возникающих в брусе, и нахождение угловых перемещений в зависимости от внешних скручивающих моментов.

При расчете валов обычно бывает известна мощность, передаваемая на вал, а величины внешних скручивающих моментов, подлежат определению. Внешние скручивающие моменты, как правило, передаются на вал в местах посадки на него шкивов, зубчатых колес и т.п.

В ряде случаев величины внешних крутящих моментов определяются по величине потребляемой мощности и по скорости вращения вала. Если вал делает в минуту n оборотов (n- частота вращения, единицы измерения — об/мин.), то вращающий момент можно найти по формуле: М_вр=P/n,

эта формула дает значение момента в Н·м, если мощность выражена в Вт, а частота вращения n — об/мин.

§2. Построение эпюр крутящих моментов

Для определения напряжений и деформаций вала необходимо знать значения внутренних крутящих моментов M_k (M_z) в поперечных сечениях по длине вала. Диаграмму, показывающую распределение значений крутящих моментов по длине бруса, называют эпюрой крутящих моментов. Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала.

В простейшем случае, когда вал нагружен только двумя внешними моментами (эти моменты из условия равновесия вала ΣM_z=0 всегда равны друг другу по величине и направлены в противоположные стороны), как показано на рис. 1, крутящий момент M_z в любом поперечном сечении вала (на участке между внешними моментами) по величине равен внешнему моменту |M₁|=|M₂|.

• Свежие записи
  • Чем отличается двухтактный мотор от четырехтактного
  • Сколько масла заливать в редуктор мотоблока
  • Какие моторы бывают у стиральных машин
  • Какие валы отсутствуют в двухвальной кпп
  • Как снять стопорную шайбу с вала

  
  

  источники:

  https://evakuatorinfo.ru/formulu-dlya-rascheta-ugla-zakruchivaniya-vala

  💥 Видео

  2 1 Кручение круглого вала К выполнению РГЗСкачать

  

  Сопромат. Практическое занятие №1.4Скачать

  

  Формулы для расчета сечения кабеля и проводаСкачать

  

  Кручение круглого стержняСкачать

  

  Определение реакций опор в балке. Сопромат.Скачать

  

  Статически неопределимый вал. Расчет на прочность при крученииСкачать

  

  Формула ЖуравскогоСкачать