Где используется цилиндр в жизни (5 видео)

Что такое цилиндр? Цилиндр (круговой цилиндр) – тело, которое состоит из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов, – образующими цилиндра

Виды цилиндров Наклонный (косой) Эллиптический

Площадь цилиндра (прямой круговой) Площадь боковой поверхности цилиндра можно вычислить, умножив длину образующей на периметр сечения цилиндра плоскостью, перпендикулярной образующей (основание). Sb = Ph P = 2πR  Sb = 2πRh. Площадь полной поверхности цилиндра равна сумме площадей его боковой поверхности и его оснований. Sp = 2πRh + 2πR2 = 2πR(h + R)

Площадь цилиндра (наклонный круговой) Для расчета площади боковой поверхности наклонного цилиндра потребуется перемножить значения образующей и периметра сечения, которое будет перпендикулярно выбранной образующей. Sбок= х Р, где х — длина образующей цилиндра, Р — периметр сечения. Сечение, кстати, лучше выбирать такое, чтобы оно образовывало эллипс. Тогда будут упрощены расчеты его периметра. Длина эллипса вычисляется по формуле, которая дает приблизительный ответ. l = π (а + в), где «а» и «в» — полуоси эллипса, то есть расстояния от центра до ближайшей и самой дальней его точек. Площадь всей поверхности нужно вычислять с помощью такого выражения: Sпол = 2 π r^2 + х Р

Объём цилиндра (прямой круговой) Объем цилиндра определяется по стандартной схеме: площадь поверхности основания умножается на высоту.

Объём цилиндра (наклонный круговой) Площадь поверхности основания умножают на расстояние между плоскостями – перпендикулярный отрезок, построенный между ними. Как видно из рисунка, такой отрезок равен произведению длины образующей на синус угла наклона образующей к плоскости.

Скошенный цилиндр Прямой круговой цилиндр со скошенным основанием либо кратко скошенный цилиндр определяют с помощью радиуса основания R, минимальной высоты h1 и максимальной высоты h2.

Где в повседневной жизни встречается цилиндр? Трубы водо- и газопроводные — те же цилиндры, только с большой длиной.

Где в повседневной жизни встречается цилиндр? Гидроцилиндры к машинах и механизмах для подачи жидкостей.

Где в повседневной жизни встречается цилиндр? Тубус для ношения чертежей.

Где в повседневной жизни встречается цилиндр? Круглый стакан, кастрюля, круглая ваза, бутылка — те же цилиндры.

Где в повседневной жизни встречается цилиндр? Архитектура

Курс профессиональной переподготовки

Содержание

Библиотечно-библиографические и информационные знания в педагогическом процессе
Охрана труда
Охрана труда
Оставьте свой комментарий
Подарочные сертификаты
Цилиндр в архитектуре
Содержимое разработки
Презентация по геометрии на тему «Цилиндр и его элементы»(11 класс)
🔍 Видео

Библиотечно-библиографические и информационные знания в педагогическом процессе

Курс повышения квалификации

Охрана труда

Курс профессиональной переподготовки

Охрана труда

Международная дистанционная олимпиада Осень 2021

Вам будут интересны эти курсы:

Оставьте свой комментарий

Минобразования Кузбасса рекомендовало техникумам и школам уйти на каникулы до 7 ноября

Большинство московских родителей поддерживают экспресс-тестирование на ковид в школах

В школе в Пермском крае произошла стрельба

Около половины детей болеют коронавирусом в бессимптомной форме

Почти все вузы в России открыли пункты вакцинации от ковида

Минпросвещения планирует прекратить прием в колледжи по 43 профессиям

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Читайте также: Главный цилиндр сцепления пежо 406 где находится

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Цилиндры ФараоновСкачать

Цилиндр в архитектуре

Презентация полезна тем, что показывает повсеместное архитектурное использование фигуры цилиндр.

Содержимое разработки

Государственное бюджетное профессиональное образовательное учреждение

«Ковровский медицинский колледж имени Е. И. Смирнова»

Специальность: «Акушерское дело»

Подготовил студент 05 – А группы

В современном мире в архитектуре начинается использование всё более новых, сложных и интересных фигур. Людям становится скучно жить среди однообразных пятиэтажных домов. Моё внимание привлёк цилиндр. Фигура не простая сама по себе, а применить её в строительстве – сложно и неоднозначно. В моей презентации я хочу рассказать Вам о том, что же такое цилиндр, поведаю о некоторых его особенностях и покажу на примере его использование в одной из главных наук мира – архитектуре.

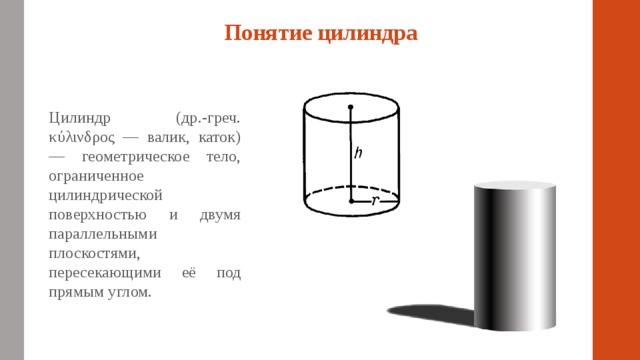
Цилиндр (др.-греч. κύλινδρος — валик, каток) — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её под прямым углом.

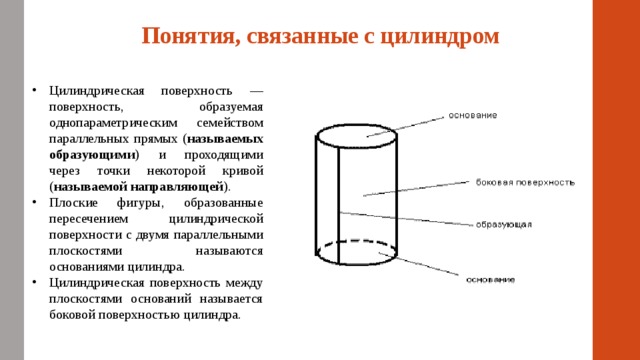
Понятия, связанные с цилиндром

Цилиндрическая поверхность — поверхность, образуемая однопараметрическим семейством параллельных прямых ( называемых образующими ) и проходящими через точки некоторой кривой ( называемой направляющей ).
Плоские фигуры, образованные пересечением цилиндрической поверхности с двумя параллельными плоскостями называются основаниями цилиндра.
Цилиндрическая поверхность между плоскостями оснований называется боковой поверхностью цилиндра.

Хронология цилиндра в архитектуре

Цилиндры в древней архитектуре

Сами цилиндры появились в архитектуре ещё в древние века, они выступали в роли несущих и второстепенных элементов. Конечно, всё началось с округлых колонн. Их применяли всё время и такой архитектурных ход был распространён. Здания же цилиндрической формы появились лишь в наше время.

Первые каменные колонны применили в Древнем Египте при постройке Пирамиды Джосера в 2650 году до н.э. Впервые в истории была применена каменная постройка из 40 колонн высотой каждой из них в 10 метров. Так как эти колонны были первыми на земле, архитектор Имхотеп соединил каждую из них со стеной с одной стороны.

Также одни из самых популярных сооружений цилиндрической формы является Колизей в Риме.

Цилиндры в современной архитектуре

Среди компонентов современной архитектуры можно найти немало кубических конструкций (особенно из стекла), треугольников в виде, например, фронтонов; и случайные изгибы тоже часто встречаются. Но что насчёт цилиндров? При их упоминании в связи со строительством зданий вспоминается стиль арт-деко, который весьма недолго был популярен в начале 20 века.

Цилиндры и закруглённые углы использовались им для передачи динамики плавных движений. В поле ретроспективы также оказываются башенки средневековых сооружений и примитивные промышленные здания Америки.

Тем не менее, цилиндры нашли себе место в современной архитектуре. Редкие образцы производят сильнейшее впечатление, если перекликаются с контекстом.

Есть два вопроса, отсутствие ответов на которые, объясняет нежелание архитекторов включать цилиндрические формы в структуру зданий, тем более жилых. Что будет находиться внутри? И как связать цилиндр с остальной частью здания эмоционально и физически?

Читайте также: Осевой цилиндр это ботаника

По первому пункту можно заметить, что внутри цилиндров обычно возводятся лестницы, которые наполняют всю конструкцию практическим смыслом. Что касается второго вопроса, здесь будут продемонстрированы здания, смежные стены которых разделены цилиндрическим элементом, который может выдаваться вперёд или стоять вровень с фасадом.

Ещё с древних времен люди использовали в строительстве цилиндрические формы зданий. Мы убедились, что непросто выбрать такой сложной фигуре своё место в архитектурном пространстве. Но, хоть это и сложно, выглядит потрясающе!

Видео:Зачем на стенках цилиндров нового двигателя наносят царапины. Хонингование, что этоСкачать

Презентация по геометрии на тему «Цилиндр и его элементы»(11 класс)

Ищем педагогов в команду «Инфоурок»

Описание презентации по отдельным слайдам:

муниципальное автономное общеобразовательное учреждение средняя общеобразовательная школа № 45 Методическое пособие для учащихся 11 классов Составил учитель математики высшей категории Гавинская Елена Вячеславовна. г.Калининград 2016-2017 учебный год

В древности при строительстве грандиозных храмов и дворцов людям приходилось таскать и носить на себе огромные валуны и колонны. Тогда и было замечено, что катать предметы намного легче и удобнее. Примерно так и появились и популяризовались цилиндры. И по сей день эти тела вращения часто встречаются в нашей жизни. В архитектуре, в технике, в мире моды – цилиндры побывали везде.

Определение. Цилиндр (греч. kýlindros, валик, каток) — геометрическое тело, ограниченное цилиндрической поверхностью (называемой боковой поверхностью цилиндра) и не более чем двумя поверхностями (основаниями цилиндра).

Другие определения цилиндра. Цилиндр — это фигура, состоящая из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Цилиндром называется тело, ограниченное замкнутой цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими эту поверхность. У Евклида цилиндр получается вращением прямоугольника. У Кавальери – движением образующей (при произвольной направляющей – «цилиндрика»).

Вклад Евклида в математику. О Евклиде почти ничего неизвестно, откуда он был родом, где и у кого учился. Папп Александрийский (III в.) сообщает, что он был очень доброжелателен ко всем тем, кто сделал хоть какой-нибудь вклад в математику, корректен, в высшей степени порядочен и совершенно лишен тщеславия. Евклид, как и другие великие греческие геометры, занимался астрономией, оптикой и теорией музыки. До нас дошли его сочинения, посвященные прикладным вопросам: «Феномены» (элементарная сферическая астрономия), «Оптика» (учение о перспективе) и «Сечение канона» ( теория музыки). Это были первые прообразы будущих исследований по математической физике: в них теория выводилась строго дедуктивно из явно сформулированных физических гипотез и математических постулатов. Гораздо больше мы знаем о математическом творчестве Евклида. Прежде всего Евклид является для нас автором «Начал», по которым учились математики всего мира. Эта удивительная книга пережила более двух тысячелетии, но до сих пор не утратила своего значения не только в истории науки, но и самой математике. Созданная там система евклидовой геометрии и теперь изучается во всех школах мира и лежит в основе почти всей практической деятельности людей. На геометрии Евклида базируется классическая механика, ее апофеозом было появление в 1687 г. Математических начал натуральной философии Ньютона, где законы земной и небесной механики и физики устанавливаются в абсолютном евклидовом пространстве. Содержание «Начал» далеко не исчерпывается элементарной геометрией — это основы всей античной математики. Здесь подводится итог более чем 300-летнему ее развитию и вместе с тем создается прочная 6aзa для дальнейших исследований. Последующие математики ссылались на предложения «Начал», как на нечто окончательно установленное.

Читайте также: Главный тормозной цилиндр замена манжетов уаз

Вклад Кавальери в математику. В своем основном труде «Геометрия» (1635г.) Кавальери развил разработанный им задолго до выхода книги новый метод определения площадей и объемов – так называемый метод неделимых. Неделимыми Кавальери называл параллельные между собой хорды плоской фигуры или параллельные плоскости тела. Важнейший признак неделимости состоит в том, что число измерений его на единицу меньше самого геометрического образа. У плоской фигуры 2 измерения, у ее неделимого, т.е. у отрезка – 1 измерение. Кавальери доказал теорему о том, что площади двух подобных фигур относятся как квадраты, а объемы – как кубы соответствующих неделимых, и установил, что отношение суммы квадратов всех неделимых треугольника к сумме квадратов всех неделимых параллелограмма, имеющего с треугольником одинаковые основания и высоту, равно 1:3. Впоследствии Кавальери нашел аналогичные соотношения для суммы кубов и т.д. до девятой степени неделимых. Труды Кавальери сыграли огромную роль в формировании исчисления бесконечно малых.

Элементы цилиндра. Круги, ограничивающие цилиндрическую поверхность называются основаниями цилиндра. Отрезки образующих, заключенные между основаниями, называются образующими цилиндра, а образованная ими поверхность – боковой поверхностью цилиндра. Ось цилиндрической поверхности называется осью цилиндра.

Свойства цилиндра. Основания равны и параллельны. Образующие равны и параллельны. Все сечения цилиндра плоскостями, параллельными плоскостям оснований цилиндра, равны основаниям цилиндра.

1. Основания циилиндра равны и параллельны. Справедливость этого утверждения следует из того, что множество концов образующих, лежащих в плоскости β, получается из окружности L параллельным переносом на вектор ОО1. Параллельный перенос является движением и, значит, наложением, а при наложении любая фигура переходит в равную ей фигуру. Следовательно, при параллельном переносе на вектор ОО1 окружность L перейдет в равную ей окружность L1 радиуса r с центром в точке О1. Доказательства свойств. α β L L1 о о1

2. Образующие цилиндра равны и параллельны. Все образующие цилиндра перпендикулярны к плоскостям оснований. Но плоскости оснований цилиндра параллельны. Значит, все образующие цилиндра – расстояния между параллельными плоскостями, следовательно, (по теореме) они равны и параллельны.

3. Все сечения цилиндра плоскостями, параллельными плоскостям оснований цилиндра, равны основаниям цилиндра. Действительно, любое такое сечение является общим основанием двух цилиндров, на которые секущая плоскость разбивает данный цилиндр. Поэтому оно равно другим основаниям этих цилиндров, которые являются основаниями исходного цилиндра.

Влияние оснований на цилиндр. Если основания цилиндра плоские (и, следовательно, содержащие их плоскости параллельны), то цилиндр называют стоящим на плоскости. Если основания стоящего на плоскости цилиндра перпендикулярны образующей, то цилиндр называется прямым. В частности, если основание стоящего на плоскости цилиндра — круг, то говорят о круговом (круглом) цилиндре; если эллипс — то эллиптическом. α β

Виды цилиндра. Бесконечное тело, ограниченное замкнутой бесконечной цилиндрической поверхностью, называется бесконечным цилиндром. Прямой круговой цилиндр — это поверхность, образованная вращением одной из параллельных прямых вокруг другой, принятой в качестве оси вращения. Бесконечное тело, ограниченное замкнутым цилиндрическим лучом и его основанием, называется открытым цилиндром. Основание и образующие цилиндрического луча называют соответственно основанием и образующими открытого цилиндра. Конечное тело, ограниченное замкнутой конечной цилиндрической поверхностью и двумя выделившими её сечениями, называется конечным цилиндром, или собственно цилиндром. Сечения называются основаниями цилиндра. По определению конечной цилиндрической поверхности, основания цилиндра равны.