Где применяется цилиндр в жизни (6 видео)

Презентация полезна тем, что показывает повсеместное архитектурное использование фигуры цилиндр.

Содержимое разработки

Государственное бюджетное профессиональное образовательное учреждение

«Ковровский медицинский колледж имени Е. И. Смирнова»

Специальность: «Акушерское дело»

Подготовил студент 05 – А группы

В современном мире в архитектуре начинается использование всё более новых, сложных и интересных фигур. Людям становится скучно жить среди однообразных пятиэтажных домов. Моё внимание привлёк цилиндр. Фигура не простая сама по себе, а применить её в строительстве – сложно и неоднозначно. В моей презентации я хочу рассказать Вам о том, что же такое цилиндр, поведаю о некоторых его особенностях и покажу на примере его использование в одной из главных наук мира – архитектуре.

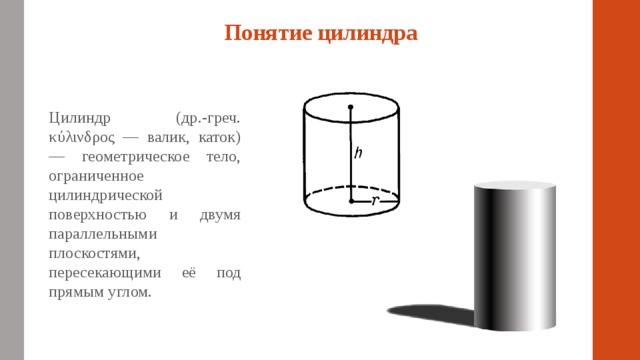
Цилиндр (др.-греч. κύλινδρος — валик, каток) — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её под прямым углом.

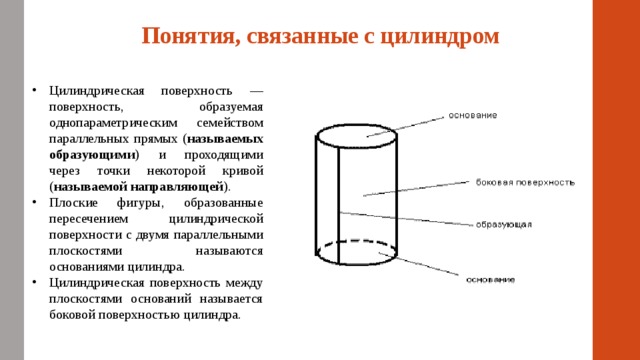
Понятия, связанные с цилиндром

Цилиндрическая поверхность — поверхность, образуемая однопараметрическим семейством параллельных прямых ( называемых образующими ) и проходящими через точки некоторой кривой ( называемой направляющей ).
Плоские фигуры, образованные пересечением цилиндрической поверхности с двумя параллельными плоскостями называются основаниями цилиндра.
Цилиндрическая поверхность между плоскостями оснований называется боковой поверхностью цилиндра.

Хронология цилиндра в архитектуре

Цилиндры в древней архитектуре

Сами цилиндры появились в архитектуре ещё в древние века, они выступали в роли несущих и второстепенных элементов. Конечно, всё началось с округлых колонн. Их применяли всё время и такой архитектурных ход был распространён. Здания же цилиндрической формы появились лишь в наше время.

Первые каменные колонны применили в Древнем Египте при постройке Пирамиды Джосера в 2650 году до н.э. Впервые в истории была применена каменная постройка из 40 колонн высотой каждой из них в 10 метров. Так как эти колонны были первыми на земле, архитектор Имхотеп соединил каждую из них со стеной с одной стороны.

Видео:Объём цилиндраСкачать

Также одни из самых популярных сооружений цилиндрической формы является Колизей в Риме.

Цилиндры в современной архитектуре

Среди компонентов современной архитектуры можно найти немало кубических конструкций (особенно из стекла), треугольников в виде, например, фронтонов; и случайные изгибы тоже часто встречаются. Но что насчёт цилиндров? При их упоминании в связи со строительством зданий вспоминается стиль арт-деко, который весьма недолго был популярен в начале 20 века.

Цилиндры и закруглённые углы использовались им для передачи динамики плавных движений. В поле ретроспективы также оказываются башенки средневековых сооружений и примитивные промышленные здания Америки.

Тем не менее, цилиндры нашли себе место в современной архитектуре. Редкие образцы производят сильнейшее впечатление, если перекликаются с контекстом.

Есть два вопроса, отсутствие ответов на которые, объясняет нежелание архитекторов включать цилиндрические формы в структуру зданий, тем более жилых. Что будет находиться внутри? И как связать цилиндр с остальной частью здания эмоционально и физически?

По первому пункту можно заметить, что внутри цилиндров обычно возводятся лестницы, которые наполняют всю конструкцию практическим смыслом. Что касается второго вопроса, здесь будут продемонстрированы здания, смежные стены которых разделены цилиндрическим элементом, который может выдаваться вперёд или стоять вровень с фасадом.

Ещё с древних времен люди использовали в строительстве цилиндрические формы зданий. Мы убедились, что непросто выбрать такой сложной фигуре своё место в архитектурном пространстве. Но, хоть это и сложно, выглядит потрясающе!

Методическая разработка урока на тему: «Тела вращения в практической деятельности и в жизни человека»

Ищем педагогов в команду «Инфоурок»

Тема урока: Тела вращения в практической деятельности и в жизни человека.

Вид занятия: Семинар «Защита темы» -мотивация познавательной деятельности студентов – показать прикладную направленность темы.

1. Обучающая: показать применение темы в практических ситуациях.

2. Развивающая: продолжить формирование умения распознавать геометрические модели тел, применять математические знания в практических ситуациях, описанных условием задачи.

3. Воспитательная: продолжить воспитание мотивации учения, раскрывая профессиональную и практическую значимость изучаемого материала.

Обеспечение занятия: компьютер, проектор, модели многогранников и круглых тел, обобщающие таблицы по теме, раздаточный материал.

Вступительная беседа. Материал этого раздела большой по объёму. Вопросы теории подробно рассмотрены нами на предыдущих занятиях.

Задача итогового занятия ещё раз подчеркнуть важность сведений о телах вращения для практики, рассмотреть историю некоторых вопросов, показать связь данного раздела с другими направлениями математики и науки.

При введении понятия «тела вращения» мы уже говорили, что большинство деталей, вытачиваемых из дерева или металла на токарных станках- тела вращения и посуда, изготавливаемая на гончарных кругах и стеклянные банки, бутылки, графины, стаканы, пробирки и различные катушки, барабаны, валы, шайбы, заклёпки, линзы, патроны, снаряды, спортивный диск, мячи, обручи- всё это материальные тела, имеющие форму тел вращения, и где бы мы не оказались, наверняка будем иметь дело с подобными телами.

Читайте также: Игрушка для кошек цилиндр погремушка чистый котик ф 4 см

Цилиндрические резервуары и цистерны, хоккейные шайбы, электроды для электросварки, круглые карандаши, цилиндр двигателя внутреннего сгорания или поршневого насоса тоже цилиндры.

Видео:Почему никто не знает об этой функции штангенциркуля?!Скачать

Естественно насыпанные на горизонтальной поверхности кучи песка, зерна, угля имеют форму конусов. При этом каждому сыпучему материалу соответствует определённый угол естественного укоса (угол уклона, образующий к плоскости основание конуса). Так, например, песку, соответствует угол укоса в 25 0 , глине- 30 0 , щебню-33 0 , углю-42 0 .

Форму усечённого конуса имеют вёдра, тарелки, кадушки, ролики многих подшипников и т.д.

Примеры материальных шаров – шарики подшипников, шарики в дробилках, многие резервуары на нефтеперерабатывающих заводах, конфеты драже, бильярдные шары.

В математике имеют место идеальные модели конуса, цилиндра и др. В реальной же практике о той или иной фигуре вращения можно говорить, что она является конусом или цилиндром с определенным приближением, именно с этим мы встречаемся на производстве.

В курсе стереометрии рассматриваются три основные тела вращения: цилиндр, конус, шар, и у нас учащиеся разделились на три группы:

Общее название этих тел связано с тем, что их образование можно связать с вращением некоторой плоской фигуры вокруг ее стороны как оси.

1 задание: Наиболее полно представить свое тело вращения, назвать все важнейшие понятия. Перечисленные понятия должны быть проиллюстрированы с помощью моделей и рисунков.

Цилиндр — одно из самых распространённых тел. Простейшим цилиндром является прямой круговой цилиндр.

Прямым круговым цилиндром называется тело, образованное вращением прямоугольника вокруг одной из его сторон.

В цилиндре можно выделить два основания, называется осью цилиндра.

Границы цилиндра составляют два основания и боковая поверхность цилиндра, ее можно представлять себе образованной вращением отрезка вокруг оси цилиндра.

Сочинением цилиндра плоскостью параллельной основанию будет круг того же радиуса, что и основания.

Высота цилиндра – это расстояние между основаниями, т.е. длина отрезка оси между центрами оснований. Обычно цилиндр задают двумя числовыми данными: радиусом основания и высоты.

Боковую поверхность цилиндра можно развернуть на плоскость, если представить себе эту поверхность, сделанной из бумаги и разрезать ее параллельные оси цилиндра, то она развернется в форме прямоугольника, одна из сторон которого равна высоте цилиндра, а другая – длине окружности основания.

Конус – коническая форма, также как и цилиндрическая, широко распространена в окружающем нас мире.

Прямым круговым конусом называется тело, образованное вращением прямоугольного треугольника вокруг одного из его катетов.

В конусе можно выделить основание в форме круга и вершину. Прямая, проходящая через вершину и центр основания, называется осью конуса.

Сечением конуса плоскостью, параллельной основанию, будет круг.

Высота конуса – это расстояние от его вершины до основания, т.е. длина отрезка оси, соединяющего вершину и центр основания.

Конус можно задать двумя численными данными, радиусом основания и высотой.

Радиус основания и высота – это катеты того прямоугольного треугольника, вращением которого был образован конус. Гипотенуза этого треугольника называется образующей конуса.

Боковая поверхность конуса образована вращением вокруг оси отрезка, один конец которого совпадает с вершиной конуса.

Так же, как и у цилиндра, боковую поверхность конуса можно развернуть на плоскость. Если разрез сделать по образующей, то разверткой будет круговой сектор.

Если в конусе провести сечение, параллельное основанию, то между основанием и плоскостью сечение получится тело, называемое усеченным конусом.

Шар и сфера – сферой радиуса R (где R >0) с центром в точке О называется множество точек пространства, удаленных от точки О на расстояние R .

Сфера разбивает пространство на две части: внутреннюю, составленную из точек, удаленных от точки О на расстояние меньшее R , и внешнюю, составленную из точек, удаленных от точки О на расстояние большее R .

Видео:Студенты российского вуза разработали вечный двигатель #вечныйдвигатель #изобретенияСкачать

Внутреннюю часть пространства вместе со сферой называют шаром радиуса R с центром в точке О. Таким образом, шар – множество точек пространства, удаленных от точки Она расстояние меньшее или равное R /

Сфера и шар радиуса R с центром в точке О получаются при вращении соответственно окружности и круга вокруг диаметра.

Отрезки, соединяющие точки с центром, называются радиусами сферы. Они же называются радиусами соответствующего шара и сферы называются отрезки, по которым шар пересекается с прямыми, проходящими через центр.

А) Преподаватель называет номер формулы. Студент показывает модель фигуры вращения, которой соответствует предлагаемая формула:

Б) С помощью структурной схемы назвать все вспомогательные понятия тел вращения.

Слово учителя: Для чего математика нужна человеку? В самом деле, почему без нее не обойтись биологу, физику, химику, астроному? Да потому, что она, как и естественные науки изучает окружающий нас мир. Разница лишь в том, что физика, биология, химия – изучают предметы и явления окружающего нас мира со стороны их качества или, как говорят, со стороны содержания, а математика изучает те же предметы со стороны их количества, пространства и времени, говорят со стороны их формы.

Читайте также: Задние тормозные цилиндры 2123 артикул

И так, следующее 3 задание заключается в сообщении учащихся по теме:

Тракторы; сельскохозяйственные машины

— поршень двигателя внутреннего сгорания состоит из цилиндрических, конических и шаровой поверхностей.

— Запальная свеча в двигателях внутреннего сгорания, предназначена для воспламенения горючего в цилиндрах двигателя, состоит из цилиндрических, винтовых и конических поверхностей, а также из шестиугольной призмы.

— Клапан двигателя внутреннего сгорания (например автомобильного, тракторного и др.) состоит из цилиндрических, конических и других поверхностей вращения.

— Рулевое колесо трактора представляет собой кольцевую поверхность.

— Искроуловитель содержит коническую, цилиндрическую и шаровую поверхности.

— Колесо комбайна – есть комбинация цилиндрических поверхностей и т.п., производится анализ примеров использования тел вращения в технических объектах:

Трансмиссионный вал со шкивом – цилиндр, на котором закреплен шкив, представляющий собой комбинацию цилиндра и усеченного конуса. Трансмиссионный вал применяется для передачи вращательного движения.

Верхняя часть домкрата имеет форму усеченного конуса, к которому примыкает бобышка (для крепления шестерни), также имеющая форму усеченного конуса.

Шариковый подшипник, широко используемый в технике, состоит из двух колец, между которыми находятся шарики. Воспринимая нагрузку, шарики одновременно катятся по желобам, проточенным на кольцах, в результате трение скольжения заменяется трением качения.

Шлифованный круг (деталь шлифованного станка) представляет собой усеченный конус.

Металлические трубы для передачи воды, газа, пара – являются полыми круговыми цилиндрами. Для закрепления труб между собой с помощью болтов служат фланцы, представляющие собой круговые цилиндры большего диаметра, но меньшей высоты.

Опрыскиватель – машина для опрыскивания растений ядохимикатами с целью защиты от болезней и вредителей.

Одним из рабочих органов опрыскивателя является резервуар, в котором транспортируется и размещается рабочая жидкость.

Этот резервуар обычно имеет форму цилиндра со сферическим днищем.

Для вычисления его объема рекомендуется формула:

D – диаметр цилиндрической части резервуара

L – длина его сферических частей (высота шаровых сегментов).

Видео:Как использовать интеграл в обычной жизни. Математик МГУ и Савватеев #shortsСкачать

Высеивающий аппарат большинства сеялок представляет собой цилиндрическую катушку с желобками.

Связь математики с организацией и технологией механизированных работ

Площадь боковой поверхности цилиндра применяется в технологии посева зерновых культур.

Учащиеся устанавливают зерновую сеялку на норму высева. Для этого они определяют число оборотов ( m ) колеса семян, необходимое для засева контрольного участка Fk с целью проверки установки сеялки на заданную норму высева по формуле: Fy =2П RH .

Если принять ширину захвата сеялки Bp = H , то участок, засеянный на один оборот колеса сеялки F об. Определяется по тем же формулам, что и на уроке геометрии.

Слово учителя : Геометрия – одна из самых гармоничных областей математики. Она очаровывает стройностью своих аксиом, покоряет строгой логикой доказательств.

За тысячелетия своего существования, математика прошла большой и сложный путь на протяжении которого неоднократно изменялся ее характер, содержание и стиль изложения.

4 задание. Исторический экскурс

История развития человечества доказала уже много раз, что математика – красивейшая наука, без которой не может развиваться ни одна другая. Продуктивнейший метод познания природы – математическое модулирование.

В математике, прежде всего, поражает удивительная универсальность ее модулей и их эффективность в применении для других наук. Правда математическая модель не всегда дает немедленную практическую отдачу. Бывает, что она оказывает полезной только через тысячу лет. Пример тому, конические сечения – линии, которые образуются при сечении кругового конуса плоскостями, не проходящими через его вершину.

Они были открыты в Древней Греции

и описаны Аполлонием Пергским ( III в. –

II в. до н.э.). Имеются три конических сечения.

Эллипс – плоскость сечения пересекает все образующие конуса.

Парабола – плоскость сечения параллельна какой-либо образующей.

Гипербола – плоскость сечения пересекает образующие обеих плоскостей конуса, т.е. обе ветви гиперболы считаются одной кривой.

Конические сечения имеют интересные оптические свойства, которые широко используются в технике.

Это основано на свойствах фокусов конических сечений-эллипса, гиперболы, параболы и поверхностей, образованных вращением этих кривых, которые широко используются в оптических приборах, например-прожекторах.

Конические сечения играют важную роль в природе, например, по эллиптическим, параболическим и гиперболическим орбитами движутся тела в поле тяготения.

Начальные сведения о свойствах тел вращения относятся ко времени зарождения геометрии, как будущей математической науки. Ещё за тысячи лет до наших времён земледельцы пытались хотя бы приблизительно узнать о собранном урожае, вычисляя размеры куч зерна и тех емкостей, где зерно хранилось

Читайте также: Пропуск зажигания 6 цилиндр n52

В связи с развитием мореплавания были нужны астрономические наблюдения, что заставляло человека изучать свойства шара и его частей.

Длительное время зависимости между геометрическими величинами, с помощью которых проводились различные вычисления, употреблялись как некоторые практические правила, без должного обоснования. Уже в УП веке до нашей эры в Греции начали накапливаться знания в области стереометрии. Вырабатывались приёмы математических рассуждений, начали формироваться общие представления о пространственных фигурах и способах доказательства их свойств.

Важная роль в изложении сведений по стереометрии в определённой логической последовательности принадлежит греческому математику Евклиду (Ш век до нашей эры), автору известного научного сочинения «Начала» состоящему из 13 книг. В 12 книге «Начал» исследуются многогранники, круглые тела – цилиндр, конус, шар, в 13 книге – правильные многогранники.

Другой знаменитый древнегреческий математик Архимед (Ш до нашей эры) в своём труде «О шаре и цилиндре» выводит формулы для определения поверхностей и объёмов этих тел, исследует свойства правильных многогранников.

Труды Евклида и Архимеда после перевода их на арабский язык, а с арабского на латинский, проникают в Европу и создают основу для составления учебников для средних школ.

Видео:Для чего необходимо торцевать цилиндры на УралеСкачать

В первой половине ХУП века в развитии геометрии происходят принципиальные изменения: в геометрии используются методы алгебры и математического анализа, которые начинают в те времена зарождаться.

Для нас и сейчас представляют интерес установленные Архимедом зависимости между площадью поверхности цилиндра и шара, объёмом цилиндра и шара определённых размеров. Примером таких утверждений Архимеда являются «…боковая поверхность описанного около шара цилиндра равна поверхности шара; объём описанного около шара цилиндра равен утроенной половине объёма шара, а полная поверхность этого цилиндра равна утроенной половине поверхности шара».

Слово учителя: Современный человек должен понимать мир в котором он живёт. А что, как не математика, позволяет нам одним ключом открыть природу самых различных явлений, познать её сущность. Не потому ли древние греки, выбирая для неё название, остановились на слове «матема», что означает «знание», и не за это ли немецкий учёный математик Гаусс назвал её «царицей наук»?

Признавая за математиков гордое царственное величие, её в то же время, называют и «слугой всех наук». С момента своего возникновения, математика всегда верно служила всем наукам.

5 задание. Задачи производственного содержания

Свободно насыпанный ворох свежеубранной пшеницы по своей форме близок к конусу с углом естественного откоса а=40.

а) Чему равен объём вороха, если его перекидка (длинна линии ASB ) равна р?

OA=1/2 p cos a, то V ₁ =1/3 П R 2 H=

=1/3 П р 2 /4 cos 2 40 0 р /2sin40 0 =

= П /24 р 3 sin 40 0 cos 2 40

Примечание : sin 40 0 =0,6 ; cos 40 0 =0,8

б) какого объёма ворох пшеницы можно насыпать на квадратной площадке со стороной 10м?

V =1/3 П R 2 H =1/3 П 5 х 4,2=110 м 3

При защите почв от водной эрозии на склонах иногда делают лунки в форме полушара диаметром d . Сколько воды может накопиться в такой лунке на склоне с углом наклона а?

Объём воды равен объёму шарового сегмента

H -высота сегмента, т.к расстояние от центра

лунки до поверхности воды ОР= d /2 sin a ,

ОР / r = sin a, то H=d/2 (1 – sin a)

Отсюда находим V = П/24 d 3 (1- sin a ) 2 (2+ sin a )

V= 1/3 П d 2 /4(1- sin a) 2 (2d/2+ d/2 sin a) = П d 2 /12(1 – sin a) 2 (2+ sin a ) d/2=

= П d 3 /24 (1 – sin a) 2 (2 + sin a)

Объём бензина в бочке (или горизонтальной цистерне) иногда находится с помощью рейки. Сколько бензина в бочке, если длина h мокрого конца рейки равна 1,9 дм, диаметр d бочки равен 7,6 дм,а её длина 1 равна 11,6 дм?

Находим, что cos ½= r — h / r =3.8-1.9/3.8=1/2( r = d /2)

А =2/3 П Cos 2/2=1/2 V=1r 2 /2 (1 – sin a) =11.6 3.8 2 /2(2/3 П sin 2/3 П )=83,8(2,09-0,87)=83,8 х 1,22

На основании полученной выше формулы для различных ёмкостей составлены так называемые ёмкостные таблицы, которыми и используются на практике.

Выделите знакомые геометрические формы на предлагаемых моделях или чертежах деталей и механизмов сельскохозяйственных машин.

Видео:Цилиндры.Скачать

Пример одной из таких задач:

Выделите на чертеже искроуловителя трактора МТЗ-80 знакомые геометрические формы. Анализ рисунка позволяет выделить следующие знакомые формы: усеченный конус, шаровой сегмент, цилиндр.

Выделить на чертеже керна (инструмент, применяемый в разметочном деле) знакомые геометрические формы (цилиндр, конус).

Заклепка- деталь служащая для скрепления двух (а иногда и более) металлических частей. (Цилиндр, часть – сегмент).

Пробойник- инструмент для пробивания отверстий в тонком листовом материале (металл-картон; цилиндр, конус)