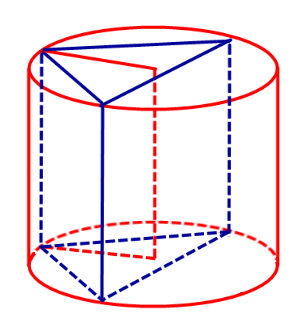
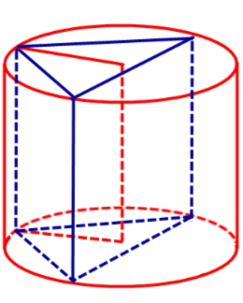
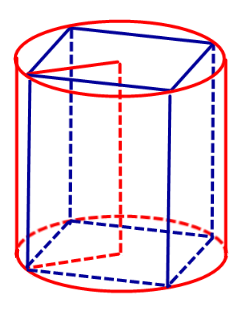
Геометрическая комбинация цилиндр призма (4 видео)

Содержание

Цилиндры, вписанные в призмы. Свойства призмы, описанной около цилиндра
Отношение объемов цилиндра и описанной около него правильной n — угольной призмы
Призмы, вписанные в цилиндры
Призмы, вписанные в цилиндр. Свойства призмы, вписанной в цилиндр
Комбинация цилиндра и призмы.
Комбинация цилиндра и призмы.
Вопрос 1. Какие условия нужны, чтобы конус был вписан в пирамиду ?
Ответ: Конус вписан в пирамиду, если его основание вписано в основание пирамиды и их вершины совпадают.
Вопрос 2 . А что значит « основание конуса вписано в основание пирамиды?»
Вопрос 3 . Как называются выделенные красным цветом отрезки на рис.1 ?
Ответ: Эти отрезки называются апофемами.
Вопрос 4. А что такое апофема?
Ответ: Это высота боковой грани пирамиды.
Задание к рис. 2 : Назовите апофемы и высоту пирамиды.
Дистанционное обучение как современный формат преподавания
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Математика: теория и методика преподавания в образовательной организации
Оставьте свой комментарий
Подарочные сертификаты
📹 Видео

Видео:Призма и цилиндр. Практическая часть. 11 класс.Скачать

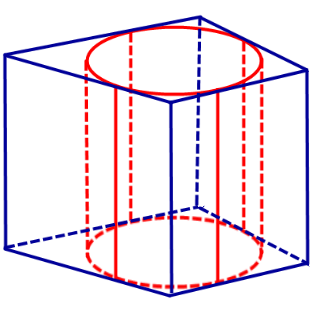
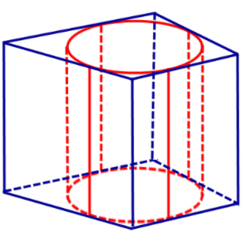
Цилиндры, вписанные в призмы. Свойства призмы, описанной около цилиндра

Определение 2. Если цилиндр вписан в призму, то призму называют описанной около цилиндра.

Прежде, чем перейти к вопросу о том, в какую же призму можно вписать цилиндр, докажем следующее свойство призм.

Утверждение 1. Если в основания призмы можно вписать окружности, то отрезок, соединяющий центры вписанных окружностей, будет параллелелен и равен боковому ребру призмы.

Рассуждая аналогичным образом, заключаем, что точка O’ равноудалена от всех прямых, на которых лежат ребра верхнего основания A’₁A’₂, A’₂A’₃, . , A_{n – 1}A_n , а поскольку O’ лежит в плоскости верхнего основания, то точка O’ является центром вписанной в многоугольник A’₁A’₂ . A’_n окружности.

В силу того, что прямые OO’ и A₁A’₁ параллельны по построению, а прямые OA₁ и O’A’ параллельны как линии пересечения двух параллельных плоскостей третьей плоскостью, замечаем, что четырехугольник OO’A₁A’₁ является параллелограммом, откуда вытекает равенство: OO’ = A₁A’₁ .

Теорема. В призму можно вписать цилиндр тогда и только тогда, когда выполнены следующие два условия:

Призма является прямой призмой;
В основания призмы можно вписать окружности.

Доказательство. Докажем сначала, что если в n – угольную призму вписан цилиндр, то оба условия теоремы выполнены.

Действительно, выполнение условия 2 следует непосредственно из определения цилиндра, вписанного в призму. Докажем, что выполняется и условие 1, т.е. докажем, что описанная около цилиндра призма является прямой призмой.

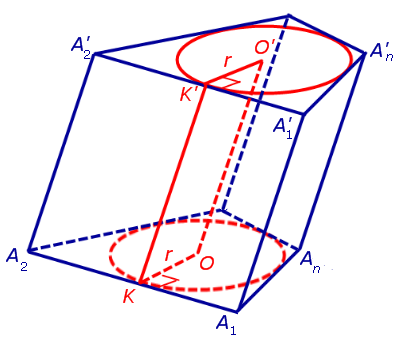
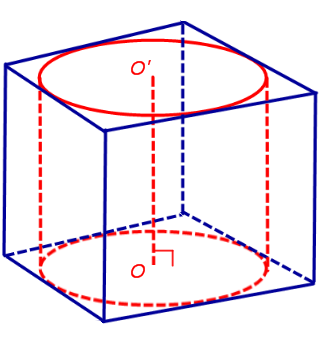
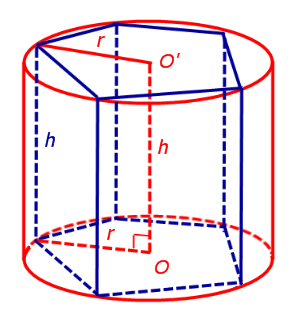
С этой целью рассмотрим ось цилиндра OO’ , соединяющую центры окружностей, вписанных в нижнее и верхнее основания призмы (рис. 3).

Согласно утверждению 1 отрезок OO’ параллелен боковым ребрам призмы. Поскольку ось цилиндра OO’ перпендикулярна к плоскостям его оснований, то и боковые ребра призмы также перпендикулярны к плоскостям оснований, то есть призма является прямой призмой.

Таким образом, мы доказали, что, если призма описана около цилиндра, то оба условия теоремы выполнены.

Теперь рассмотрим прямую n – угольную призму высоты h, в основания которой можно вписать окружности, и докажем, что в такую призму можно вписать цилиндр.

Читайте также: Два вертикальных сообщающихся цилиндра заполнены водой

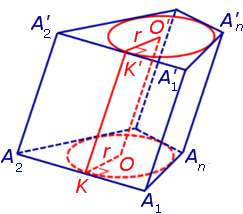
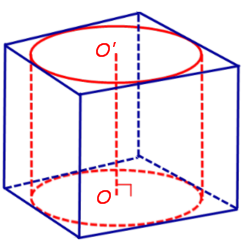
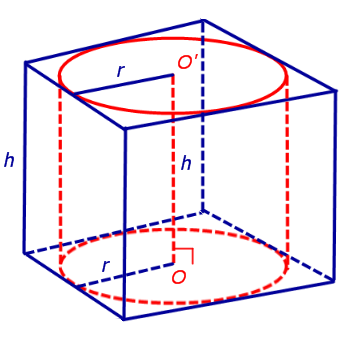
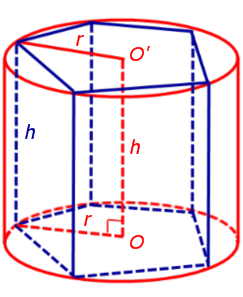
Обозначим буквой O центр окружности радиуса r, вписанной в нижнее основание призмы, а символом O’ обозначим центр окружности, вписанной в верхнее основание призмы (рис. 4).

Поскольку многоугольники, лежащие в основаниях призмы равны, то и радиусы вписанных в них окружностей будут равны. Согласно утверждению 1 отрезок OO’ параллелен и равен боковому ребру призмы. Так как рассматриваемая призма прямая, то ее боковые ребра перпендикулярны плоскости основания и равны высоте призмы h. Значит, и отрезок OO’ перпендикулярен плоскости основания призмы и равен h.

Цилиндр с осью OO’ , радиусом r и высотой h и будет вписан в исходную призму.

Доказательство теоремы завершено.

Следствие 1 . Высота призмы, описанной около цилиндра, равна высоте цилиндра.

Следствие 2. В любую прямую треугольную призму можно вписать цилиндр.

Справедливость этого утверждения вытекает из того факта, что в любой треугольник можно вписать окружность.

Следствие 3. В любую правильную n – угольную призму можно вписать цилиндр.

Для доказательства этого следствия достаточно заметить, правильная призма является прямой призмой. Основаниями правильной призмы являются правильные многоугольники, а в любой правильный n – угольник можно вписать окружность.

Видео:Комбинации тел. Урок 10. Геометрия 11 классСкачать

Отношение объемов цилиндра и описанной около него правильной n — угольной призмы

Задача. Найти отношение объемов цилиндра и описанной около него правильной n — угольной призмы.

Решение. Поскольку и объем цилиндра, и объем призмы объем призмы вычисляются по формуле

а высота цилиндра равна высоте описанной около него призмы, то для объемов цилиндра и описанной около него правильной n — угольной призмы справедливо равенство

Следствие 4. Отношение объема цилиндра к объему описанной около него правильной треугольной призмы правильной треугольной призмы равно

Следствие 5. Отношение объема цилиндра к объему описанной около него правильной четырехугольной призмы правильной четырехугольной призмы равно

Следствие 6. Отношение объема цилиндра к объему описанной около него правильной шестиугольной призмы равно

Видео:Геометрия 11 класс (Урок№15 - Комбинации многогранников и круглых тел.)Скачать

Призмы, вписанные в цилиндры

Видео:Комбинации тел многогранники, цилиндр, конус, шар. Урок 10. Геометрия 11 классСкачать

Призмы, вписанные в цилиндр. Свойства призмы, вписанной в цилиндр

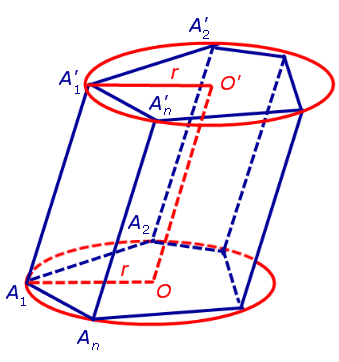
Определение 1. Призмой, вписанной в цилиндр, называют такую призму, основания которой вписаны в окружности оснований цилиндра, а боковые ребра призмы являются образующими цилиндра (рис. 1).

Определение 2. Если призма вписана в цилиндр, то цилиндр называют описанным около призмы.

Прежде, чем перейти к вопросу о том, какую призму можно вписать в цилиндр, докажем следующее свойство призм.

Утверждение 1. Если около оснований призмы можно описать окружности, то отрезок, соединяющий центры описанных окружностей, будет параллелелен и равен боковому ребру призмы.

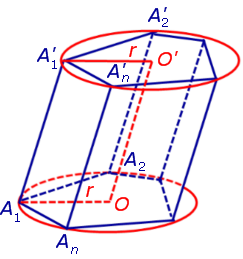
Докажем, что точка O’ является центром окружности радиуса r, описанной около верхнего основания призмы. С этой целью рассмотрим, например, четырехугольник A₁A’₁O’O (рис. 2).

Рассуждая аналогичным образом, заключаем, что

то есть точка O’ – центр окружности радиуса r , описанной около верхнего основания призмы.

В силу того, что четырехугольник OO’A₁A’₁ является параллелограммом, получаем равенство

Читайте также: Цилиндр духовенства 9 букв

Теорема. Около призмы можно описать цилиндр тогда и только тогда, когда выполнены следующие два условия:

Призма является прямой призмой;
Около оснований призмы можно описать окружности.

Доказательство. Докажем сначала, что если около n – угольной призмы описан цилиндр, то оба условия теоремы выполнены.

Действительно, выполнение условия 2 следует непосредственно из определения цилиндра, описанного около призмы. Из этого определения также следует, что вписанная в цилиндр призма является прямой призмой, поскольку образующие цилиндра перпендикулярны к плоскостям его оснований,

Таким образом, мы доказали, что, если призма вписана в цилиндр, то оба условия теоремы выполнены.

Теперь рассмотрим прямую n – угольную призму высоты h, около оснований которой можно описать окружности, и докажем, что около такой призмы можно описать цилиндр.

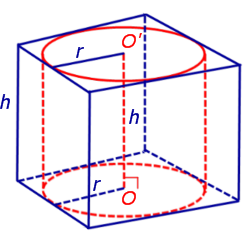
Обозначим буквой O центр окружности радиуса r, описанной около нижнего основания призмы, а символом O’ обозначим центр окружности, описанной около верхнего основания призмы.

Поскольку многоугольники, лежащие в основаниях призмы равны, то и радиусы описанных около них окружностей будут равны. Согласно утверждению 1 отрезок OO’ параллелен и равен боковому ребру призмы. Так как рассматриваемая призма прямая, то ее боковые ребра перпендикулярны плоскости основания и равны высоте призмы h. Значит, и отрезок OO’ перпендикулярен плоскости основания призмы и равен h.

Цилиндр с осью OO’ , радиусом r и высотой h и будет описан около исходной призмы.

Доказательство теоремы завершено.

Следствие 1. Высота призмы, вписанной в цилиндр, равна высоте цилиндра.

Следствие 2. Около любой прямой треугольной призмы можно описать цилиндр (рис. 4).

Следствие 3. Около любого прямоугольного параллелепипеда (в частности, около куба прямоугольного параллелепипеда (в частности, около куба ) можно описать цилиндр (рис. 5).

Замечание 1. Если у прямоугольного параллелепипеда прямоугольного параллелепипеда три ребра, выходящие из одной вершины, равны a, b, c и различны, то существует три возможности описать около этого параллелепипеда цилиндр в зависимости от того, какое из ребер параллелепипеда выбрано в качестве образующей описанного цилиндра (рис. 6, 7, 8).

Видео:Видеоурок по математике "Цилиндр"Скачать

Комбинация цилиндра и призмы.

Ищем педагогов в команду «Инфоурок»

Видео:Миникурс по геометрии. Куб, призма, цилиндр и конусСкачать

Комбинация цилиндра и призмы.

Какие условия нужны, чтобы одна геометрическая фигура была вписана в другую геометрическую фигуру стереометрии;

Что такое высота и апофема;

Теорему Пифагора для решения задач;

Вычислять нужную величину с помощью теоремы Пифагора;

Сделать необходимый чертёж к решению задачи;

Применять свойства геометрических фигур к условиям задачи;

развивать интерес к предмету;

усвоить материал по теме урока;

развивать у учащихся умение концентрироваться, слушать, а так же логическое мышление, речь, внимание, воображение.

воспитывать системность, самостоятельность, этику взаимоотношений.

Оборудование: Компьютер. Материалы к уроку: 4 рисунка комбинации пирамиды и конуса, рисунки к новому материалу « комбинация цилиндра и призмы».

Тип урока: комбинированный.

Актуализация знаний учащихся. Подготовка к активной учебно-познавательной деятельности на основном этапе урока.

Рис. 1

Вопрос 1. Какие условия нужны, чтобы конус был вписан в пирамиду ?

Ответ: Конус вписан в пирамиду, если его основание вписано в основание пирамиды и их вершины совпадают.

Вопрос 2 . А что значит « основание конуса вписано в основание пирамиды?»

Ответ: Это значит, что стороны основания пирамиды должны быть касательными к окружности основания конуса.

Читайте также: Как сделать летающий цилиндр из бумаги

Вопрос 3 . Как называются выделенные красным цветом отрезки на рис.1 ?

Ответ: Эти отрезки называются апофемами.

Вопрос 4. А что такое апофема?

Ответ: Это высота боковой грани пирамиды.

Рис. 2

Задание к рис. 2 : Назовите апофемы и высоту пирамиды.

Ответ: Апофемами являются отрезки SK и SM , а высотой пирамиды является

Рис 3.

Вопрос к рис.3 : А как можно описать конус вокруг пирамиды?

Ответ: Нужно условие совпадение вершин и теперь основание пирамиды должно быть вписано в основание конуса – то есть все вершины основания пирамиды должны лежать на окружности основания конуса.

В случае треугольной и шестиугольной пирамиды эти условия так же выполняются.(Смотреть ответ на вопрос к рис.3)

Решение задачи из учебника № 630.

Новая тема урока: Комбинация цилиндра и призмы.

Цилиндр вписан в призму (или призма описана около цилиндра), если основания цилиндра вписаны в соответствующие основания призмы. Очевидно, что их высоты совпадут.

Вывод: цилиндр можно вписать в призму, если призма прямая, а в ее основание можно вписать окружность. И призму можно вписать в цилиндр с теми же условиями.

Следующая задача:

Сегодня на уроке мы разобрали комбинации призмы и цилиндра, а также решили задачи по теме: цилиндр, описанный вокруг шестиугольной призмы и цилиндр, описанный вокруг прямой четырёхугольной призмы.

Домашнее задание : учебник стр. 146 задача № 634.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Номер материала: ДБ-1523608

Международная дистанционная олимпиада Осень 2021

Вам будут интересны эти курсы:

Оставьте свой комментарий

Минобрнауки утвердило перечень олимпиад для школьников на 2021-2022 учебный год

В школе в Пермском крае произошла стрельба

Школьников не планируют переводить на удаленку после каникул

В Хабаровске утвердили дополнительные школьные каникулы

Школьных охранников предлагают обучать основам психологии

Почти все вузы в России открыли пункты вакцинации от ковида

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.