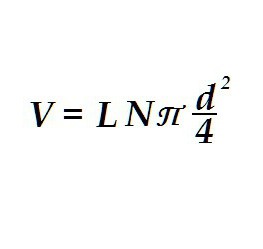Геометрические фигуры формы цилиндров (5 видео)

Название науки «геометрия» переводится как «измерение земли». Зародилась стараниями самых первых древних землеустроителей. А было так: во время разливов священного Нила потоки воды иногда смывали границы участков земледельцев, а новые границы могли не совпасть со старыми. Налоги же крестьянами уплачивались в казну фараона пропорционально величине земельного надела. Измерением площадей пашни в новых границах после разлива занимались специальные люди. Именно в результате их деятельности и возникла новая наука, получившая развитие в Древней Греции. Там она и название получила, и приобрела практически современный вид. В дальнейшем термин стал интернациональным названием науки о плоских и объёмных фигурах.

Планиметрия – раздел геометрии, занимающийся изучением плоских фигур. Другим разделом науки является стереометрия, которая рассматривает свойства пространственных (объёмных) фигур. К таким фигурам относится и описываемая в этой статье – цилиндр.

Примеров присутствия предметов цилиндрической формы в повседневной жизни предостаточно. Цилиндрическую (гораздо реже – коническую) форму имеют почти все детали вращения — валы, втулки, шейки, оси и т.д. Цилиндр широко используется и в строительстве: башни, опорные, декоративные колонны. А кроме того посуда, некоторые виды упаковки, трубы всевозможных диаметров. И наконец – знаменитые шляпы, ставшие надолго символом мужской элегантности. Список можно продолжать бесконечно.

Содержание

Определение цилиндра как геометрической фигуры
Виды цилиндров
Что такое поверхность вращения
Площадь поверхности цилиндра
Определение объёма фигуры
Как построить развёртку цилиндра
Отличия скошенного цилиндра
Геометрические характеристики скошенного цилиндра
Знакомство с геометрическим телом — Цилиндром.
Конспект занятия (ФЭМП) «Цилиндр»
📸 Видео

Видео:Фигуры и формы - 1984Скачать

Определение цилиндра как геометрической фигуры

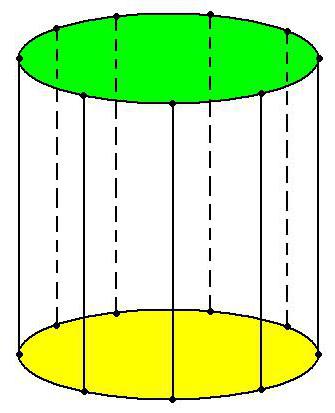
Цилиндром (круговым цилиндром) принято называть фигуру, состоящую из двух кругов, которые при желании совмещаются с помощью параллельного переноса. Именно эти круги и являются основаниями цилиндра. А вот линии (прямые отрезки), связывающие соответствующие точки, получили название «образующие».

Важно, что основания цилиндра всегда равны (если это условие не выполняется, то перед нами – усечённый конус, что-либо другое, но только не цилиндр) и находятся в параллельных плоскостях. Отрезки же, соединяющие соответствующие точки на кругах, параллельны и равны.

Совокупность бесконечного множества образующих — не что иное, как боковая поверхность цилиндра – один из элементов данной геометрической фигуры. Другая её важная составляющая – рассмотренные выше круги. Называются они основаниями.

Видео:Объемные Геометрические ФИГУРЫ Загадки для ДЕТЕЙСкачать

Виды цилиндров

Самый простой и распространённый вид цилиндра – круговой. Его образуют два правильных круга, выступающих в роли оснований. Но вместо них могут быть и другие фигуры.

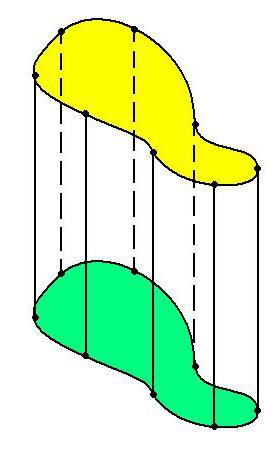
Основания цилиндров могут образовывать (кроме кругов) эллипсы, другие замкнутые фигуры. Но цилиндр может иметь не обязательно замкнутую форму. Например основанием цилиндра может служить парабола, гипербола, другая открытая функция. Такой цилиндр будет открытым или развернутым.

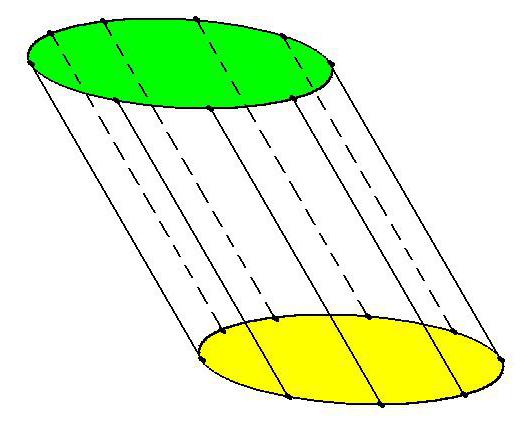
По углу наклона образующих к основаниям цилиндры могут быть прямыми или наклонными. У прямого цилиндра образующие строго перпендикулярны плоскости основания. Если данный угол отличается от 90°, цилиндр – наклонный.

Видео:ТЕМА 2. ПОСТРОЕНИЕ КУБА, ЦИЛИНДРА, ШАРАСкачать

Что такое поверхность вращения

Прямой круговой цилиндр, без сомнения – самая распространённая поверхность вращения, используемая в технике. Иногда по техническим показаниям применяется коническая, шарообразная, некоторые другие типы поверхностей, но 99% всех вращающихся валов, осей и т.д. выполнены именно в форме цилиндров. Для того чтобы лучше уяснить, что такое поверхность вращения, можно рассмотреть, как же образован сам цилиндр.

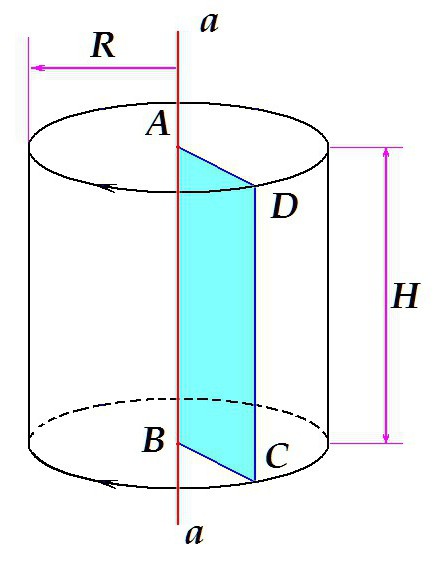
Допустим, имеется некая прямая a, расположенная вертикально. ABCD – прямоугольник, одна из сторон которого (отрезок АВ) лежит на прямой a. Если вращать прямоугольник вокруг прямой, как это показано на рисунке, объём, который он займёт, вращаясь, и будет нашим телом вращения – прямым круговым цилиндром с высотой H = AB = DC и радиусом R = AD = BC.

В данном случае, в результате вращения фигуры — прямоугольника — получается цилиндр. Вращая треугольник, можно получить конус, вращая полукруг – шар и т.д.

Видео:Миникурс по геометрии. Куб, призма, цилиндр и конусСкачать

Площадь поверхности цилиндра

Для того чтобы вычислить площадь поверхности обычного прямого кругового цилиндра, необходимо подсчитать площади оснований и боковой поверхности.

Вначале рассмотрим, как вычисляют площадь боковой поверхности. Это произведение длины окружности на высоту цилиндра. Длина окружности, в свою очередь, равняется удвоенному произведению универсального числа П на радиус окружности.

Площадь круга, как известно, равняется произведению П на квадрат радиуса. Итак, сложив формулы для площади определения боковой поверхности с удвоенным выражением площади основания (их ведь два) и произведя нехитрые алгебраические преобразования, получаем окончательное выражение для определения площади поверхности цилиндра.

Видео:Учим фигуры. Урок 4. Развивающее видео для детей (учим формы – раннее развитие ребенка)Скачать

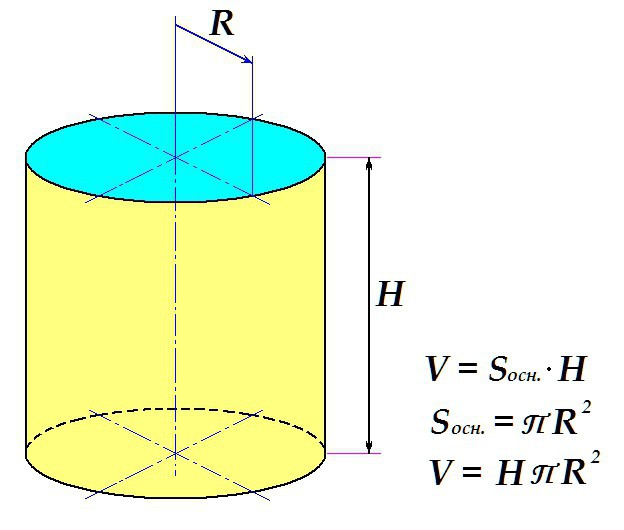
Определение объёма фигуры

Объем цилиндра определяется по стандартной схеме: площадь поверхности основания умножается на высоту.

Таким образом, конечная формула выглядит следующим образом: искомое определяется как произведение высоты тела на универсальное число П и на квадрат радиуса основания.

Читайте также: Mitsubishi не работают два цилиндра

Полученная формула, надо сказать, применима для решения самых неожиданных задач. Точно так же, как объем цилиндра, определяется, например, объём электропроводки. Это бывает необходимо для вычисления массы проводов.

Отличия в формуле только в том, что вместо радиуса одного цилиндра стоит делённый надвое диаметр жилы проводки и в выражении появляется число жил в проводе N. Также вместо высоты используется длина провода. Таким образом рассчитывается объем «цилиндра» не одного, а по числу проводков в оплётке.

Такие расчёты часто требуются на практике. Ведь значительная часть ёмкостей для воды изготовлена в форме трубы. И вычислить объем цилиндра часто бывает нужно даже в домашнем хозяйстве.

Однако, как уже говорилось, форма цилиндра может быть разной. И в некоторых случаях требуется рассчитать, чему равен объем цилиндра наклонного.

Отличие в том, что площадь поверхности основания умножают не на длину образующей, как в случае с прямым цилиндром, а на расстояние между плоскостями – перпендикулярный отрезок, построенный между ними.

Как видно из рисунка, такой отрезок равен произведению длины образующей на синус угла наклона образующей к плоскости.

Видео:Геометрические тела.Скачать

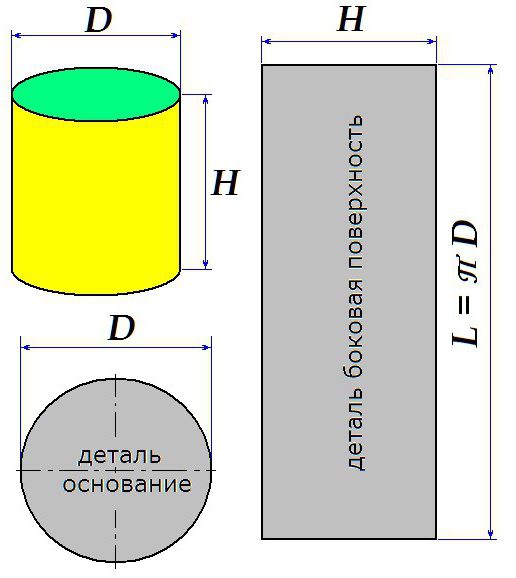
Как построить развёртку цилиндра

В некоторых случаях требуется выкроить развёртку цилиндра. На приведённом рисунке показаны правила, по которым строится заготовка для изготовления цилиндра с заданными высотой и диаметром.

Следует учитывать, что рисунок приведен без учёта швов.

Видео:песня формы | геометрические фигуры для детей | типы фигур | учить формы | Shape SongСкачать

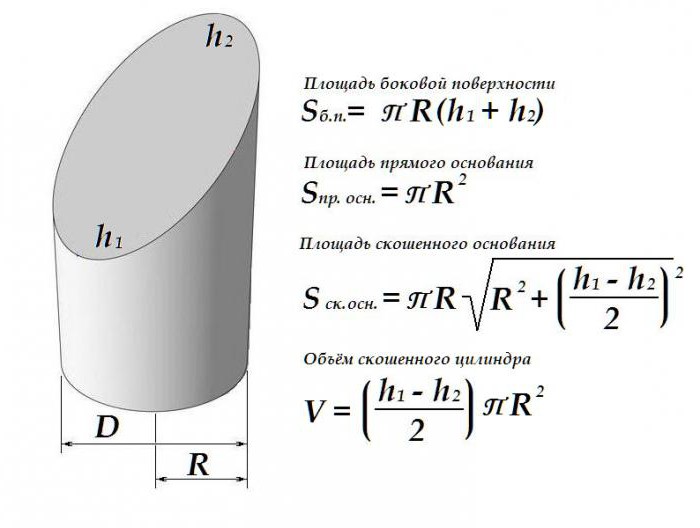
Отличия скошенного цилиндра

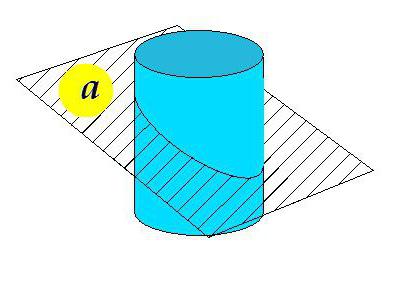
Представим себе некий прямой цилиндр, ограниченный с одной стороны плоскостью, перпендикулярной образующим. А вот плоскость, ограничивающая цилиндр с другой стороны, не перпендикулярна образующим и не параллельна первой плоскости.

На рисунке представлен скошенный цилиндр. Плоскость а под неким углом, отличным от 90° к образующим, пересекает фигуру.

Такая геометрическая форма чаще встречается на практике в виде соединений трубопроводов (колена). Но бывают даже здания, построенные в виде скошенного цилиндра.

Видео:Видеоурок по математике "Цилиндр"Скачать

Геометрические характеристики скошенного цилиндра

Наклон одной из плоскостей скошенного цилиндра слегка изменяет порядок расчёта как площади поверхности такой фигуры, так и ее объёма.

Видео:Объёмные геометрические фигуры. Куб. Цилиндр. Конус. Шар // Математика 1 классСкачать

Знакомство с геометрическим телом — Цилиндром.

Екатерина Искаева
Знакомство с геометрическим телом — Цилиндром.

Задачи: 1. Формировать представление о цилиндре, умение распознавать цилиндр в предметах окружающей обстановки.

2. Закреплять счет в пределах 5, геометрические представления детей, умение находить общие свойства предметов.

Материал: картинки с изображением предметов цилиндрической формы, цилиндры разного диаметра и высоты, карточки с «паспортом» цилиндра, модели цилиндров и кубик, цифры 1 – 5, набор геометрических фигур на каждого ребенка.

1. Знакомство с цилиндром и его свойствами.

Воспитатель показывает картинки предметов цилиндрической формы: стакан, колбасу, шляпу-цилиндр, банку цилиндрической формы, клеящий карандаш.

— Что общего у всех этих предметов вы заметили? (У всех предметов похожа форма.)

Если дети затрудняются ответить на этот вопрос, можно задать наводящие вопросы: одинаков ли материал, из которого сделаны эти предметы, их цвет, размер, назначение.

Затем воспитатель сообщает детям, что предметы такой формы называются цилиндрами, и просит их найти цилиндры на своем столе. Вместе с цилиндрами на столе должны быть предметы и других форм (например, шара, параллелепипеда, конуса). Целесообразно показать также картинки, на которых предметы цилиндрической формы являются элементами: пушка, здание с колоннами, дерево и т. д.

Далее дети знакомятся со свойствами цилиндра.

— Знаете ли вы, почему цилиндр так называется? Очень давно, когда никаких машин еще не было, люди передвигали тяжелые предметы при помощи стволов деревьев. Подумайте – как?

Воспитатель дает детям несколько цилиндров одинакового диаметра (например, карандаши) и кубик и предлагает представить, что кубик – это очень тяжелый груз, который надо переместить с одного конца стола на другой, используя цилиндры. После выполнения задачи воспитатель рассказывает, что слово «цилиндр» в переводе с греческого – «каток», «валик». Одним из его свойств является то, что его можно катить.

Детям предлагается разойтись по группе и найти предметы цилиндрической формы.

Затем дети возвращаются к столу, на котором стоят разные цилиндры. Им предлагается найти фигуры, одинаковые по какому-либо признаку, и у отобранных фигур найти признаки отличия. Например, это могут быть цилиндры, равные по высоте, но разные по толщине, цвету, материалу, из которого они сделаны (цилиндры можно сделать из бумаги, пластилина, взять пластмассовые, металлические цилиндры, деревянные карандаши и т. д.)

2. Физкультминутка: «Кто самый внимательный?»

По команде «Ухо» дети должны схватиться за ухо (можно усложнить, говоря «Правое ухо», по команде «Нос» — за нос. Воспитатель выполняет задание вместе с детьми. Через некоторое время начинает намеренно ошибаться и сбивать детей.

3. Игра: «Паспортный стол».

Читайте также: Можно ли растачивать гильзы блока цилиндров

У детей на столах карточки от 1 до 5. Воспитатель предлагает им рассмотреть фигуры, сделанные из пластилина различных цветов.

Дети отвечают на вопросы воспитателя:

— Сколько всего фигур? (Показывают цифру.)

— Посчитайте от 1 до 5 и от 5 до 1.

— Сколько цилиндров? (Хлопают в ладоши.)

— Почему хлопнули 4 раза? (Вторая фигура – не цилиндр.)

— Чем вторая фигура отличается от остальных?

После всех рассуждений дети приходят к выводу, что у цилиндра с двух сторон одинаковые круги, а у второй фигуры – нет.

Воспитатель ставит цилиндр на стол и просит детей присесть так, чтобы фигура была на уровне глаз. Спрашивает детей о том. что они видят, как это можно зарисовать. Затем поворачивает цилиндр несколько раз и спрашивает детей о том же. В результате обсуждения приходят к выводу:

— Значит, если хотят рассказать о цилиндре, это делают так:

Это «паспорт» фигуры. О чем по нему можно узнать? (О высоте цилиндра, его толщине).

Воспитатель прикладывает цилиндр к прямоугольнику, а основания цилиндра – к кругам и показывает, как «паспорт» сопоставляется с его обладателем.

На столе у детей разные цилиндры. Каждому ребенку дается «паспорт», по которому он должен найти соответствующий этому «паспорту» цилиндр.

4. Игра: «Числовое лото».

Дети раскладывают на столе карточки с цифрами от 1 до 5 (лицом вниз). Карточки перемешиваются. Затем каждый ребенок должен вытащить наугад какую-нибудь карточку и выложить столько фигур «Геометрического лото», имеющих общий признак, сколько указывает цифра на карточке (например, 3 большие фигуры, или 4 красные фигуры, или 2 круга и т. д.).

После выполнения задания дети с воспитателем ходят по группе и проверяют правильность решения.

Требования к уровню подготовки воспитанников по дисциплине «Математика» во второй младшей группе. Количество и счёт: Счёт наизусть в пределах пяти, сравнивать группы предметов, содержащие до 5 предметов, сравнивать количество предметов,.

Видео:Геометрические тела. Раннее развитие. Шар, куб, цилиндр, конус.Скачать

Конспект занятия (ФЭМП) «Цилиндр»

Виктория Проскурякова
Конспект занятия (ФЭМП) «Цилиндр»

Образовательная область: «Познание»

Раздел: ФЭМП

Тема: «Цилиндр»

Цель: Познакомить детей с геометрическим телом – цилиндр на основе обследования зрительно – осязательным путем.

О. З. : Учить детей называть свойства цилиндра, классифицировать по различным признакам

и соотносить форму предметов с геометрическими фигурами.

Р. З. : Развивать познавательный интерес у детей;

В. З. : Воспитывать интерес к познавательно-исследовательской деятельности, самостоятельность, активность.

Словарная работа: цилиндр.

Билингвальный компонент: тело – денесі.

Оборудование: картинки-подсказки, на которых изображены стакан, колбаса, шляпа-цилиндр, банка цилиндрической формы, клей-карандаш, 5 карандашей на каждого ребёнка, листы белой бумаги, цилиндры, цветные карандаши.

Воспитатель: Проскурякова В. Г.

деятельности Действия воспитателя Действия детей

побудительный — Ребята, посмотрите, кто-то потерял цилиндр!

-Но это не простой цилиндр, а волшебный. Цилиндр можно обнять пальцами руки или ладонью?

-Ребята, а раз мы можем обнять предмет, значит, у него есть объём.

Цилиндр – это объёмная фигура.

-Может, попробуем произнести волшебное заклинание?

Пальчиковая игра «Магические слова»

-Ребята, после произнесения волшебного «заклинания» в цилиндре, появилось интересное задание, но очень трудное задание – которое, мы с вами должны выполнить, составить паспорт геометрическому телу «цилиндр».

Паспорт – это документ, в котором мы должны рассказать и перечислить все о цилиндре. Значит, чтобы составить «паспорт» мы должны узнать все тайны и секреты геометрического тела – цилиндр. Дети внимательно слушают воспитателя.

Дети отвечают на вопросы воспитателя.

Произносят волшебное заклинание.

сжимают — разжимают пальцы

бьют кулачок о кулачок, развести руки

поисковый -Ребята, посмотрите в нашем «волшебном цилиндре» появились картинки-подсказки.

На картинках изображены стакан, колбаса, шляпа-цилиндр, банка цилиндрической формы, клей-карандаш.

— Что общего вы заметили на этих картинках?

— Действительно, у всех предметов похожая форма.

— Одинаков ли материал, из которого сделаны эти предметы?

Их размер? Цвет? Назначение?

-Ребята, предметы такой формы называются цилиндрами.

Цилиндром меня называют, друзья.

Похож на стаканчик с мороженым я.

Похож на колонну в старинном соборе,

Похож на бревно и на столбик в заборе.

-Как называется эта фигура?

— Цилиндр можно прокатить?

— Цилиндр можно поставить?

-Найдите цилиндры на своих столах.

-Теперь обратите внимание на картинки, на которых предметы цилиндрическойформы являются элементами: пушка, здание с колоннами, дерево, круглые столбы.

— Знаете ли вы, почему цилиндр так называется?

Очень давно, когда никаких машин ещё не было, люди передвигали тяжёлые предметы при помощи стволов деревьев. Подумайте – как?

-Ребята, вы берёте пять цилиндров одинакового диаметра (карандаши).

Представьте, что кубик- это очень тяжёлый груз, который надо переместить с одного конца стола на другой, используя цилиндры. Вы убедились, что цилиндр, оказывается, может катиться.

Читайте также: Рабочей поверхности гильзы цилиндра

Слово «цилиндр» в переводе с греческого – «каток», «валик».

Одним из его свойств является то, что его можно катить.

— Ребята, предлагаю найти предметы цилиндрической формы в группе.

-Посмотрите на столе, стоят разные цилиндры.

-Ребята, я предлагаю найти цилиндры, одинаковые по какому-либо признаку, и назвать и показать признаки отличия.

Например, цилиндры, равные по высоте,

но они могут быть разные по толщине, цвету, материалу, из которых,они сделаны: из бумаги, пластилина, взять пластмассовые, металлические, деревянные.

— Значит, с помощью таких цилиндров можно перемещать груз, так как у цилиндра с двух сторон одинаковые круги. Оказывается, цилиндр прячет с двух сторон геометрическую фигуру — круг. Круг – это плоская геометрическая фигура. Вы, конечно, помните, что цилиндр можно обнять пальцами руки или ладонью, а раз мы можем обнять предмет, значит, у него есть объём.

Цилиндр – это объёмная фигура.

— Я поставлю цилиндр на стол, а вы присядьте так, чтобы фигура была на уровне глаз.

-Ребята, что вы видите и как это можно зарисовать?

-А теперь поворачиваю цилиндр несколько раз, что вы видите?

— Значит, если хотят рассказать о цилиндре,это делают так:

-О чём по нему можно узнать?

О высоте цилиндра, его толщине.

-Ребята, если приложить цилиндр к прямоугольнику в центре цилиндра спряталась геометрическая фигура – прямоугольник, а основания цилиндра – к кругам и таким образом, мы составили «паспорт» его обладателя.

У вас на столах разные цилиндры.

-Ребята, каждый из вас должен составить с «паспорт», своего цилиндра. Прикладываете цилиндр к центру листка, обводите цилиндр карандашом — получается прямоугольник, затем поворачиваете цилиндр и обводите карандашом круги и раскрашиваете таким же цветом, как и ваш цилиндр.

-Вот и готовы «паспорта». Дети рассматривают картинки и называют их.

Цилиндр можно прокатить.

Цилиндр можно поставить.

Дети знакомятся со свойствами цилиндра.

Дети внимательно слушают воспитателя.

Дети называют предметы похожие на цилиндр.

Дети находят цилиндры равные по высоте, но отличающиеся другими признаками и называют их.

Дети выполняют движения согласно стихотворному тексту.

После всех рассуждений дети приходят к выводу о том, что у цилиндра с двух сторон одинаковые круги.

Дети отвечают на вопросы воспитателя.

Дети составляют «паспорт», обводят цилиндр и раскрашивают геометрические фигуры, из которых состоит цилиндр.

корригирующий — Что нового мы узнали сегодня?

-Как вы думаете, смогли мы составить «паспорт» цилиндра и все узнать о геометрическом теле – цилиндр?

— Если да – то покажите зеленую ладошку, если нет – то красную. Отвечают на вопросы. Оценивают свою работу.

Знать: геометрическое тело – цилиндр.

Иметь: представления о классификации цилиндра по признакам соотнесения к формам геометрических фигур.

Уметь: называть предметы похожие на цилиндр, находить признаки и качества цилиндра зрительно – осязательным способом.

Конспект занятия (ФЭМП) «Число 17» йымдастырылан оу рекетіні технологиялык картасы. Технологическая карта организованной.

Конспект интегрированного занятия по ФЭМП «Число 4» Цель занятия: Познакомить с образованием числа 4 и цифрой 4; учить считать в пределах 4; соотносить числительное с каждым из предметов;.

Конспект открытого занятия по ФЭМП Образовательные области: Коммуникации, Познание. Разделы: Художественная литература, Математика. Цели: упражнять детей в узнавании и назывании.

Конспект занятия по ФЭМП Цель: Развивать у детей чувство времени, умение вычленять из окружающего характерные для того или иного времени суток признаки. Развитие.

Конспект занятия по ФЭМП в младшей группе Общая тема: «Мой детский сад» Тема : Закрепление понятий : «один», «много», «множество». Знакомство с понятием «ни одного» Цели. Учить детей.

Конспект занятия по ФЭМП в младшей группе ДОУ Общая тема: «Зима» Тема: Знакомство с числом «три» Цели. Познакомить с числом «три» и его образованием. Учить считать до трех на основе сравнения.

Конспект занятия по ФЭМП в подготовительной группе. Программное содержание: Обучающие задачи: • Продолжать учить решать простые арифметические задачи. • Упражнять в счёте в пределах 10 в.

Конспект занятия по ФЭМП в средней группе Конспект занятия по ФЭМП в средней группе НЕПОСРЕДСТВЕННАЯ ОБРАЗОВАТЕЛЬНАЯ ДЕЯТЕЛЬНОСТЬ В СРЕДНЕЙ ГРУППЕ Цель: Развитие познавательной активности.

Конспект занятия в средней группе на тему: Геометрическая фигура цилиндр. Сравнение предметов по ширине. Конспект занятия в средней группе на тему: «Геометрическая фигура цилиндр. Сравнение предметов по ширине. Цели: Учить сравнивать предметы.

Мастер-класс по изготовлению карнавальных костюмов «Новогодний цилиндр» Мастер класс «Новогодний цилиндр». Для работы нужно: — 2 листа чёрного плотного картона; — ножницы; — карандаш; — циркуль; — степлер;.