Гиперболический цилиндр второго порядка формула

Видео:Поверхности второго порядкаСкачать

Поверхности второго порядка: их виды, уравнения, примеры

Видео:Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

Общее уравнение поверхности второго порядка и инварианты поворота и переноса декартовой прямоугольной системы координат

Общее уравнение поверхности второго порядка имеет вид

Для определения вида поверхности второго порядка по общему уравнению и приведения общего уравнения к каноническому, нам понадобятся выражения, которые называются инвариантами. Инварианты — это определители и суммы определителей, составленные из коэффициентов общего уравнения, которые не меняются при переносе и повороте системы координат. Эти инварианты следующие:

Следующие два выражения, называемые семиинвариантами, являются инвариантами поворота декартовой прямоугольной системы координат:

В случае, если I 3 = 0 , K 4 = 0 , семиинвариант K 3 будет также и инвариантом переноса; в случае же I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 = 0 семиинвариант K 2 = 0 будет также и инвариантом переноса.

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Виды поверхностей второго порядка и приведение общего уравнения поверхности второго порядка к каноническому

I. Если I 3 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 , λ 2 , λ 3 — корни характеристического уравнения

В зависимости от того, какие знаки у чисел λ 1 , λ 2 , λ 3 и K 4 /I 3 , определяется вид поверхности второго порядка.

Эллипсоид

Если числа λ 1 λ 2 , λ 3 одного знака, а K 4 /I 3 имеет знак им противоположный, то общее уравнение поверхности второго порядка определяет эллипсоид.

После решения характеристического уравнения общее уравнение можно переписать в следующем виде:

Читайте также: Расчет объема цилиндра в цилиндре формула

Тогда полуоси эллипсоида будут

Поэтому каноническое уравнение эллипсоида имеет вид

Мнимый эллипсоид

Если числа λ 1 λ 2 , λ 3 и K 4 /I 3 одного знака, то общее уравнение поверхности второго порядка определяет мнимый эллипсоид.

После решения характеристического уравнения общее уравнение можно привести к каноническому уравнению мнимого эллипсоида:

Мнимый конус

Если числа λ 1 λ 2 , λ 3 , а K 4 = 0 , то общее уравнение поверхности второго порядка определяет мнимый конус.

После решения характеристического уравнения общее уравнение можно привести к каноническому уравнению мнимого конуса:

Однополостный гиперболоид

Если два корня характеристического уравнения имеют один знак, а третий корень и K 4 /I 3 имеют знак, им противоположный, то общее уравнение поверхности второго порядка определяет однополостный гиперболоид.

Обозначая в этом случае через λ 1 и λ 2 корни характеристического уравнения, имеющие один знак, общее уравнение можно переписать в виде:

то каноническое уравнение однополостного гиперболоида будет иметь вид

Двуполостный гиперболоид

Если два корня характеристического уравнения и K 4 /I 3 имеют один и тот же знак, а третий корень характеристического уравнения им противоположный, то общее уравнение поверхности второго порядка определяет двуполостный гиперболоид.

Обозначая в этом случае через λ 1 и λ 2 корни, имеющие один знак, общее уравнение можно переписать в виде:

Последняя запись и есть каноническое уравнение двуполостного гиперболоида.

Конус

Если два корня характеристического уравнения имеют один знак, третий корень имеет знак, им противоположный, а K 4 = 0 , то общее уравнение поверхности второго порядка определяет конус.

Считая, что одинаковый знак имеют корни λ 1 и λ 2 , общее уравнение можно переписать в виде:

известном как каноническое уравнение конуса.

II. Если I 3 = 0 , а K 4 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

Читайте также: Подъемный цилиндр камаз 6520

где λ 1 и λ 2 — отличные от нуля корни характеристического уравнения.

Эллиптический параболоид

Если λ 1 и λ 2 имеют один знак, то общее уравнение поверхности второго порядка определяет эллиптический параболоид.

Общее уравнение можно переписать в виде:

Выбирая перед корнем знак, противоположный знаку λ 1 и λ 2 , и полагая

получим каноническое уравнение эллиптического параболоида:

Гиперболический параболоид

Если λ 1 и λ 2 имеют разные знаки, то общее уравнение поверхности второго порядка определяет гиперболический параболоид.

Обозначая через λ 1 положительный корень, а через λ 2 — отрицательный и беря перед корнем знак минус, переписываем уравнение в виде:

получим каноническое уравнение гиперболического параболоида:

III. Если I 3 = 0 , а K 4 = 0 , I 2 ≠ 0 то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 и λ 2 — отличные от нуля корни характеристического уравнения.

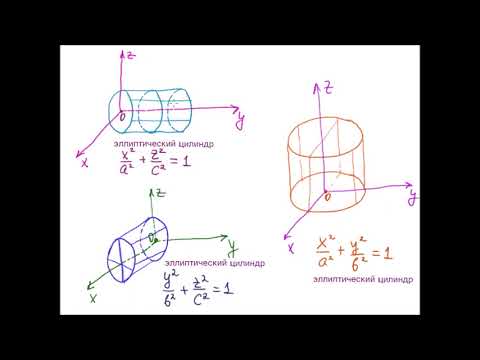
Эллиптический цилиндр

Если λ 1 и λ 2 одного знака, а K 3 /I 2 имеет знак, им противоположный, то общее уравнение поверхности второго порядка определяет эллиптический цилиндр.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

получим каноническое уравнение эллиптического цилиндра:

Мнимый эллиптический цилиндр

Если λ 1 , λ 2 и K 3 /I 2 одного знака, то общее уравнение поверхности второго порядка определяет мнимый эллиптический цилиндр.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

Последняя запись — каноническое уравнение мнимого эллиптического цилиндра.

Мнимые пересекающиеся плоскости

Если λ 1 и λ 2 имеют один знак, а K 3 = 0 , то общее уравнение поверхности второго порядка определяет две мнимые пересекающиеся плоскости.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

получим каноническое уравнение мнимых пересекающихся плоскостей:

Гиперболический цилиндр

Если λ 1 и λ 2 имеют разные знаки, а K 3 ≠ 0 , то общее уравнение поверхности второго порядка определяет гиперболический цилиндр.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

Читайте также: Передние тормозные цилиндры газ 2410

Таким образом, каноническое уравнение гиперболического цилиндра:

Пересекающиеся плоскости

Если λ 1 и λ 2 имеют разные знаки, а K 3 = 0 , то общее уравнение поверхности второго порядка определяет две пересекающиеся плоскости.

Переписываем уравнение, получившееся после решения характеристического уравнения, в виде:

Таким образом, пересекающихся плоскостей:

IV. Если I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 ≠ 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

где λ 1 = I 1 — отличный от нуля корень характеристического уравнения.

Параболический цилиндр

Уравнение, получившееся после решения характеристического уравнения, можно переписать в виде:

Это уравнение параболического цилиндра, в каноническом виде оно записывается так:

V. Если I 3 = 0 , K 4 = 0 , I 2 = 0 , K 3 = 0 , то общее уравнение поверхности второго порядка при помощи поворота и переноса прямоугольной системы координат может быть приведено к следующему виду:

Параллельные плоскости

Если K 2 , то общее уравнение поверхности второго порядка определяет две параллельные плоскости.

Мнимые параллельные плоскости

Если K 2 > 0 , то общее уравнение поверхности второго порядка определяет две мнимые параллельные плоскости.

Совпадающие плоскости

Если K 2 = 0 , то общее уравнение поверхности второго порядка определяет две совпадающие плоскости:

Видео:Поверхности второго порядка. Поверхности вращенияСкачать

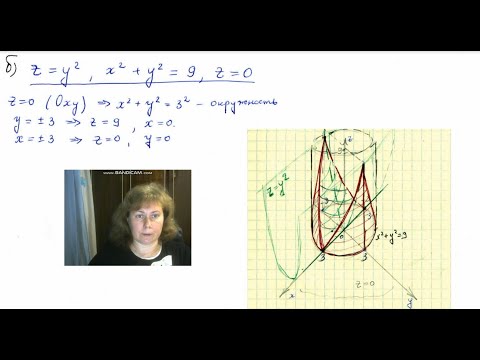
Решение примеров на определение вида поверхности второго порядка

Пример 1. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением

Следовательно, данная поверхность — однополостный гиперболоид.

Составляем и решаем характеристическое уравнение:

Пример 2. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением

Следовательно, общее уравнение определяет эллиптический параболоид.

Решаем характеристическое уравнение:

Пример 3. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением

Так как I 3 = К 4 = 0 , I 2 > 0 , I 1 K 3 , то данное общее уравнение определяет эллиптический цилиндр.

Определить вид поверхности второго порядка самостоятельно, а затем посмотреть решение

Пример 4. Определить вид и составить каноническое уравнение поверхности, заданной относительно прямоугольной системы координат общим уравнением

📸 Видео

Лекция. Гиперболоиды, параболоиды, конус. Исследование методом сечений.Скачать

§63 Цилиндрические поверхностиСкачать

Поверхности 2го порядка. КлассификацияСкачать

Цилиндрические поверхностиСкачать

Лекция 31.2. Кривые второго порядка. Гипербола.Скачать

Линейная алгебра Практика 12 Кривые второго порядкаСкачать

Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертежСкачать

Пенской А. В. - Аналитическая геометрия - Поверхности второго порядкаСкачать

Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Аналитическая геометрия, 7 урок, Линии второго порядкаСкачать

Поверхности 2-го порядка | Лекция 14 | ЛинАл | СтримСкачать

Лекция 31.1. Кривые второго порядка. ЭллипсСкачать

Неполное уравнение второго порядка. Эллипс, гипербола. ЗадачиСкачать

Кривые второго порядкаСкачать

Образование поверхностей перемещением кривых, 1973Скачать