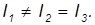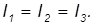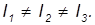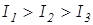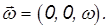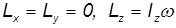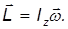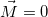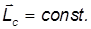Главные оси инерции цилиндр (2 видео)

Если какое-либо тело привести во вращение относительно произвольной оси и затем предоставить самому себе, то положение оси вращения в пространстве, вообще говоря, изменится: ось будет либо поворачиваться, либо перемещаться относительно инерциальной системы отсчета. Для того, чтобы произвольно взятую ось удерживать в неизменном положении, к ней необходимо приложить определенные силы.

Ось вращения тела, положение которой в пространстве сохраняется без приложения извне каких-либо сил, называется свободной осью тела.

Можно показать, что существуют по крайне мере три взаимно перпендикулярные оси, проходящие через центр масс тела, которые могут служить свободными осями. Такие оси называются главными осями инерции тела.

Моменты инерции тела относительно главных осей называются главными моментами инерции.

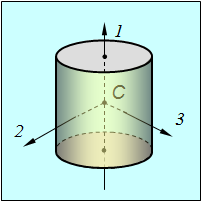
Для тел, обладающих осевой симметрией (например, у однородного цилиндра), одна из главных осей совпадает с осью симметрии, а две любые оси, перпендикулярные к оси симметрии и друг другу и проходящие через центр масс тела, также являются главными (рис. 7.15). Моменты инерции относительно двух последних осей равны друг другу, а момент инерции относительно оси симметрии отличен от них

Такое тело называется симметричным волчком.

Рис. 7.15. Главные оси однородного цилиндра

У тела с центральной симметрией (например, у однородного шара) любые три взаимно перпендикулярные оси, проходящие через центр симметрии, являются главными. Для них

Такие тела называются шаровыми волчками. Любая ось шарового волчка, проходящая через центр симметрии, является главной (а, значит, и свободной).

В общем случае главные моменты инерции тела различны, то есть

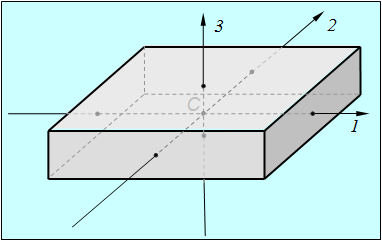
Такое тело называется асимметричным волчком. Примером асимметричного волчка может служить однородный прямоугольный параллелепипед (рис. 7.16).

Рис. 7.16. Главные оси однородного параллелепипеда

При «почти» свободном вращении на тело могут действовать малые возмущения. Если при таких возмущениях ось вращения мало изменяет свое положение, то вращение называется устойчивым. В противном случае говорят о неустойчивом вращении.

Пусть для асимметричного волчка для определенности имеет место следующее соотношение между главными моментами инерции:

Можно показать, что вращение вокруг осей 1 и 3 (то есть осей с максимальными и минимальными моментами инерции) будет устойчивым, а вокруг оси 2 (с промежуточным по величине моментом инерции) — неустойчивым.

Видео 7.4. Устойчивость полета в воздухе прямоугольного параллелепипеда

Пусть тело вращается вокруг одной из главных осей, например, вокруг оси z. Тогда вектор угловой скорости имеет вид

Компоненты момента импульса тела будут равны

То есть этом случае момент импульса параллелен оси вращения

Видео 7.5. Устойчивое вращение стержня, диска и цепочки вокруг той свободной оси, которой соответствует максимальный момент инерции

Если тело вращается в отсутствие внешних сил (), то согласно закону сохранения момента импульса в этом случае

В общем случае вектор угловой скорости вращается вокруг момента импульса. Однако если ось вращения совпадает с одной из главных осей, то ось вращения сохраняет свою ориентацию в пространстве в отсутствие внешних сил.

Читайте также: Тормозной цилиндр ваз 2105 самоподводящийся

Содержание

Савельев И.В. Курс общей физики, том I
Титульный лист
Предисловие к четвертому изданию
Из предисловия к четвертому изданию
6.6. Главные оси инерции и главные моменты инерции
💥 Видео

Видео:Урок 94. Вычисление моментов инерции телСкачать

Савельев И.В. Курс общей физики, том I

Загрузить всю книгу

Видео:Геометрические характеристики. Моменты инерции. Радиусы инерции. Сопромат.Скачать

Титульный лист

Главная редакция физико-математической литературы

Механика, колебания и волны,

Главная цель книги — познакомить студентов прежде всего с основными идеями и методами физики. Особое внимание обращено на разъяснение смысли физических законов и на сознательное применение их. Несмотря на сравнительно небольшой объем, книга представляет собой серьезное руководство, обеспечивающее подготовку, достаточную для успешного усвоения в дальнейшем теоретической физики и других физических дисциплин.

Видео:Расчет момента инерции цилиндраСкачать

Предисловие к четвертому изданию

При подготовке к настоящему изданию книга была значительно переработана. Написаны заново (полностью или частично) параграфы 7, 17, 18, 22, 27, 33, 36, 37, 40, 43, 68, 88. Существенные добавления или изменения сделаны в параграфах 2, 11, 81, 89, 104, 113.

Ранее, при подготовке ко второму и третьему изданиям были написаны заново параграфы 14, 73, 75. Существенные изменения или добавления были внесены в параграфы 109, 114, 133, 143.

Таким образом, по сравнению с первым изданием облик первого тома заметно изменился. Эти изменения отражают методический опыт, накопленный автором последние десять лет преподавания обшей физики в Московском инженерно-физическом институте.

Видео:Момент инерцииСкачать

Из предисловия к четвертому изданию

Предлагаемая вниманию читателей книга представляет собой первый том учебного пособия по курсу общей физики для втузов. Автор в течение ряда лет преподавал общую физику в Московском инженерно-физическом институте. Естественно поэтому, что пособие он писал имея в виду прежде всего студентов инженерно-физических специальностей втузов.

При написании книги автор стремился познакомить учащихся с основными идеями и методами физической науки, научить их физически мыслить. Поэтому книга не является по своему характеру энциклопедичной, содержание в основном посвящено тому, чтобы разъяснить смысл физических законов и научить сознательно применять их. Не осведомленности читателя по максимально широкому кругу вопросов, а глубоких знаний фундаментальным основам физической пауки — вот что стремился добиться автор.

Видео:Моменты инерции простейших фигур. Оси центральные и главные. Что это и где. #сопроматСкачать

6.6. Главные оси инерции и главные моменты инерции

6.6. ГЛАВНЫЕ ОСИ ИНЕРЦИИ И ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ

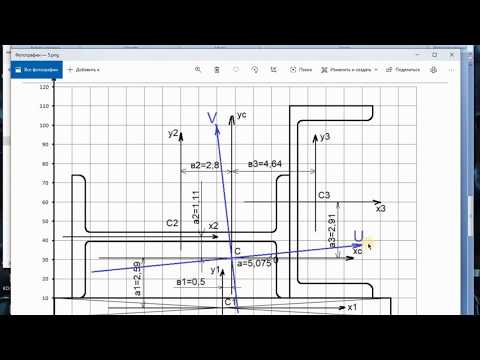
При изменении угла α значения Iz1, Iy1, Iz1y1 (6.13) изменяются, и при некотором значении угла α0 они принимают экстремальные значения. Взяв первую производную по углу α от формул (6.13) и приравняв ее нулю, получим: Эта формула определяет положение двух осей, относительно одной из которых осевой момент максимален, а относительно другой – минимален. Такие оси называют главными. Моменты инерции относительно главных осей называют главными моментами инерции. Их вычисляют следующим образом: Главные оси обладают следующими свойствами: центробежный момент инерции относительно них равен нулю; моменты инерции относительно главных осей экстремальны; для симметричных сечений оси симметрии являются главными. Главные оси, проходящие через центр тяжести фигуры, называют главными центральными осями инерции. Пример 6.4. Определить, каким образом изменяется момент инерции квадратного сечения при его повороте. Решение. Момент инерции относительно повернутой оси: Поскольку оси z, y квадрата являются осями симметрии, то есть главными, то центробежный момент инерции относительно них Izy = 0: Выводы. 1. Моменты инерции квадратного сечения с изменением положения центральных осей остаются постоянными. 2. В квадрате и других правильных многоугольниках (треугольниках, пятиугольниках) любая центральная ось является и главной. Такие фигуры называют фигурами равного сопротивления. Пример 6.5. Для фигуры, представленной в примере 6.1, определить главные центральные моменты инерции. Решение. Расстояния между центральной осью составной фигуры и собственными центральными осями элементов Моменты инерции относительно центральных осей, параллельных основанию и высоте a1= y1 – yC = 5 – 3,5 = 1,5 см; a2= y2 – yC = 1 – 3,5 = –2,5 см; b1= z1 – zC = 1 – 2,5 = –1,5 см; b2= z2 – zC = 5 – 2,5 = 2,5 см. Центробежный момент инерции Направления главных осей инерции Угол α0 (положительный) откладываем против хода часовой стрелки от оси с большим моментом инерции, то есть zC . Величины главных центральных моментов инерции