При решении задач по кинематике и динамики поступательного движения необходимо обратить внимание на классические законы Ньютона и границы их применения. Решая задачи, связанные с работой и энергией, повторить определения этих понятий. Необходимо понять сущность различия задач, решаемых с применением закона сохранения энергии и закона сохранения импульса. Рассматривая задачи на вращательное движение, следует обратить внимание на аналогию законов вращательного и поступательного движений, на то, что момент инерции характеризует геометрию распределения масс и не зависит от момента силы, обратить внимание на закон сохранения момента импульса.
Основные законы и формулы
| Скорость мгновенная | или |
| Ускорение: Тангенциальное | |
| Нормальное | |
| Полное | |
| Скорость угловая | |
| Ускорение угловое | |
| Уравнения равнопеременного вращательного движения | |
| Связь между линейными и угловыми величинами, характеризующими движение точки по окружности | |
| Второй закон Ньютона для поступательного движения при m = const | |
| Количество движения тела (импульс) | |
| Закон сохранения импульса для изолированной системы тел | |
| Работа переменной силы на пути S | |
| Мощность | |
| Кинетическая энергия тела | |
| Закон сохранения механической энергии | |
| Момент инерции материальной точки | |
| Момент инерции системы материальных точек | |
| полого и сплошного цилиндра радиуса R, цилиндра радиуса R, цилиндра радиуса R | |
| шара радиуса R | |
| стержня длины l | |
| Теорема Штейнера | |
| Момент силы относительно оси вращения | |
| Основные уравнения динамики вращательного движения | |
| тоже при I=const | |
| Закон сохранения момента количества движения | |
| Кинетическая энергия вращающегося тела | |
| Работа при вращательном движении | |
| Зависимость массы частицы от скорости | |
| Энергия покоя частицы | |
| Полная энергия частицы, движущейся со скоростью v , сравнимой со скоростью света | |
| Кинетическая энергия релятивистской частицы |
Примеры решения задач
Пример 1. Тело массой 1кг под действием постоянной силы, движется прямолинейно. Зависимость пути, пройденного телом, от времени задано уравнением S=2t 2 +4t+1. Определить работу силы за 10с от начала её действия и зависимость кинетической энергии от времени.
Сила, действующая на тело, по второму закону Ньютона равна:
Мгновенное ускорение определяется первой производной от скорости по времени или второй производной от пути по времени. В соответствии с этим:
Подставив (5) и (6) в уравнение (1), получим:
По этой формуле вычислим работу, совершаемую силой за 10с. С начала её действия:
Кинетическая энергия равна:
Ответ: A = 960 Дж, T = 8m (t + 1) 2
Пример 2. Сплошной цилиндр массой 0,5кг и радиусом 0,02м вращается относительно оси, совпадающей с осью цилиндра, по закону φ =12+8t-0,5t 2 . На цилиндр действует сила, касательная к поверхности. Определить эту силу и тормозящий момент.
Дано : m=0,5кг; r=0,02 м; φ =12+8t-0,5t 2
Решение: Цилиндр вращается относительно оси, совпадающей c его осью, по закону φ =12+8t-0,5t 2 . Угловое ускорение определяется как вторая производная от угла поворота по времени:
где ω — угловая скорость, равная первой производной от угла по времени: ; т.е. ω =8 — t , тогда
Момент силы относительно оси вращения: , или в скалярном виде: M=Fr· sinα , т.к. сила действует касательно к поверхности, то sinα =1 , тогда M=Fr и
Тормозящий момент можно определить из основного уравнения динамики вращательного движения:
где I — момент инерции цилиндра, относительно оси вращения, т.к. ось вращения совпадает с осью цилиндра, то момент инерции его равен:
Ответ: F = -0,005 Н, M = -10 -4 Hм
Пример 3 . Определить импульс и кинетическую энергию электрона, движущегося со скоростью 0,7с ( c — скорость света в вакууме).
Дано: m 0 =9,1· 10 -31 кг; ν =0,7с; с=3· 10 8 м/с
Решение: Импульсом частицы называется произведение массы частицы на скорость её движения:
Так как скорость электрона близка к скорости света, то необходимо учесть зависимость массы от скорости, определяемую по формуле:
где m — масса движущей частицы, m 0 — масса покоящейся частицы.
Подставляем (2) в (1) получим:
Сделаем подстановку числовых значений, входящих в формулу (3):
Кинетическая энергия T в релятивистской механике определяется как разность между полной энергией частицы E=mc 2 и её энергией покоя E 0 =m 0 c 2 , т.е. с учётом (2):
Найдём численное значение Т , подставив числовые данные в формулу (4):
Ответ: P = 2,675· 10 -22 кг· м/c, T = 3,28· 10 -14 Дж
Задачи для самостоятельного решения
1. При прямолинейном движении тела массой 1кг изменение его координаты со временем происходит по закону x=5t-10t 2 . Найти силу, действующую на тело.
2. Тело массой 3кг движется с ускорением, изменяющимся по закону a=10t-10 , v 0 =0. Определить силу, действующую на тело через 3 с после начала её действия и скорость тела в конце третьей секунды.
3. Тело движется под действием постоянной силы 15Н . Зависимость координаты от времени имеет вид: x=10-5t+2t 2 . Найти массу тела.
4. Найти зависимость скорости от времени и силу, действующую на тело массой 0,1кг в конце третьей секунды, если координата со временем изменяется по закону x=2t-t 2 +3t 3 .
5. Тело массой 2кг движется со скоростью, зависимость которой от времени выражается уравнением v=2,5t 2 +10t . Определить путь, пройденный телом за 5с и силу, действующую на тело в конце пятой секунды.
6. Сплошной шарик массой 400г и радиусом 5см вращается вокруг своей оси, проходящей через его центр. Закон вращения шара имеет вид: φ =4+2t-2t 2 . Определить вращающий момент.
7. Стержень массой 1кг и длиной 1м вращается вокруг своей оси, проходящей через один из его концов, по закону φ =2+t+t 2 . Определить момент силы, действующий на другой его конец.
8. Сплошной диск массой 0,2кг вращается вокруг своей оси, проходящей через центр его масс, под действием момента сил 0,8· 10 -2 Нм . Закон вращения имеет вид: φ =5-t+2t 2 . Определить радиус диска.
9. Полый цилиндр вращается относительно оси, совпадающей с осью цилиндра. Закон вращения имеет вид: φ =10-5t+0,5t 2 . Определить момент инерции и массу цилиндра, если его радиус 0,05м . Момент силы относительно оси вращения, действующий на цилиндр, равен 0,75Нм .
10. Шар и сплошной цилиндр имеют одинаковую массу 5кг и катятся с одинаковой скоростью 10м/с . Найти кинетические энергии этих тел.
11. Масса движущегося протона 2,25· 10 -27 кг. Найти скорость и кинетическую энергию протона.
12. Электрон прошёл ускоряющую разность потенциала 100 МВ . Во сколько раз его релятивистская масса больше массы покоя. Вычислить его полную и кинетическую энергии.
13. Определить скорость протона, если его релятивистская масса в три раза больше массы покоя. Вычислить кинетическую и полную энергии.
14. Вычислить скорость, полную и кинетическую энергии протона в тот момент, когда его масса равна массе α — частицы ( m 0α =6,44· 10 -27 кг ).
15. Найти импульс, полную и кинетическую энергии электрона, движущегося со скоростью, равной 0,9с .
16. Протон прошёл ускоряющую разность потенциалов, после чего его масса стала равна половине массы α — частицы ( m 0α =6,44· 10 -27 кг ). Определить разность потенциалов.
17. С какой скоростью движется электрон, если его кинетическая энергия равна 1,78МэВ ? Определить импульс электрона.
18. Кинетическая энергия частицы оказалась равной её энергии покоя. Какова скорость этой частицы?
19. При какой скорости масса любой частицы вещества в 5 раз больше его массы покоя?
20. Во сколько раз масса движущегося электрона, обладающего кинетической энергией 1МэВ больше его массы покоя?
21. Сплошной цилиндр массой 10кг катится без скольжения с постоянной скоростью 10м/с . Определить кинетическую энергию цилиндра и время его остановки, если на него подействует сила 50Н .
22. Стержень массой 2кг и длиной 1м может вращаться вокруг оси, проходящей через его середину перпендикулярно стержню. В конец стержня попадает пуля массой 10г , летящая перпендикулярно оси и стержню со скоростью 500м/с . Определить угловую скорость, с которой начнет вращаться стержень, если пуля застрянет в нем.
23. Сплошной шар, скатывается по наклонной плоскости, длина которой 10м и угол наклона 30°. Определить скорость шара в конце наклонной плоскости.
24. Полый цилиндр массой 2кг катится по горизонтальной поверхности со скоростью 20м/с . Определить силу, которую необходимо приложить к цилиндру, чтобы остановить его на пути 1,6м .
25. Маховик, имеющий форму диска массой 30кг и радиусом 10см , был раскручен до частоты 300 мин -1 . Под действием силы трения диск остановился через 20с . Найти момент силы трения, считая его постоянным.
26. Автомобиль массой 5т движется равнозамедленно, при этом в течении десяти секунд его скорость уменьшается от 72км/час до 54км/час . Найти силу торможения.
27. Тело массой 1кг под действием постоянной силы движется прямолинейно. Зависимость пути, пройденного телом, от времени выражается уравнением S=t 2 +2t+2 . Определить работу силы за 5с после начала её действия.
28. В каком случае двигатель автомобиля совершит большую работу (во сколько раз): разгон с места до скорости 36км/час или увеличение скорости от 36км/час до 72км/час ? Силу сопротивления и время движения в обоих случаях считать одинаковыми.
29. Тело массой 2кг под действием постоянной силы движется и зависимость пути, пройденного телом, от времени выражается уравнением: S=t 2 +2t+2 . Найти зависимость кинетической энергии от времени и её значение в конце второй секунды.
30. Найти силу тяги, развиваемую мотором автомобиля, движущегося в гору с ускорением 1м/с 2 . Уклон горы равен 1м на каждые 25м пути. Масса автомобиля 9,8· 10 2 кг . Коэффициент трения равен 0,1.
Качественные задачи
31. Зависимость пройденного пути от времени s(t) для двух материальных точек, движущихся прямолинейно, представлена кривыми 1 и 2 (рис.1). Спрашивается, какая кривая соответствует возрастанию скорости точки, а какая — убывающей скорости?
32. Поперек реки, скорость течения которой , плывет лодка. Скорость лодки относительно воды направлена под углом к линии, перпендикулярной течению реки. Под каким углом относительно той же линии движется лодка?
33. Материальная точка движется по спирали. При этом нормальное ускорение постоянно: аn=сonst. Как изменяются линейная и угловая скорости?
34. В какую сторону вдоль оси вращения Земли направлен вектор угловой скорости при суточном её вращении?
35. Вектор угловой скорости диска направлен на восток при вращении относительно горизонтальной оси. Указать направление линейной скорости точек обода диска?
36. Пуля массой m , летящая горизонтально, попадает в подвешенный на шнуре предмет массы М . При этом возможны три случая: 1) пуля застревает в предмете, 2) пуля пробивает предмет и сохраняет только часть своей энергии, 3) пуля после удара отскакивает от предмета. В каком из этих случаев предмет поднимется на большую высоту и в каком — на наименьшую?
37. Зависит ли скорость тела у основания наклонной плоскости от угла, который она составляет с горизонтом при наличии трения или без него при скатывании этого тела без начальной скорости?
38. Два шара одинаковой массы сталкиваются (абсолютно упругий удар), испытывая нецентральный удар. Доказать, что угол между направлениями скоростей шаров после удара составляет угол 90 0 ?
39. Зависимость потенциальной энергии тел от их положения изображается параболой W p =bx 2 . По какому закону изменяются силы, действующие на эти тела?
40. У вертолетов, кроме несущего винта, на хвостовой части имеется дополнительный винт. Поясните, зачем нужен этот винт?
41. Как можно найти емкость сосуда, используя только весы и набор гирь?
42. Цилиндрический стакан до краёв наполнен жидкостью. Каким образом содержимое стакана разделить на две равные части, имея меньший сосуд произвольной формы?
43. Определите диаметр мяча линейкой.
44. Автомобиль спускается с горы с выключенным двигателем. За счет какой энергии движется автомобиль при этом?
45. Два шара разной массы, имеющие одинаковые кинетические энергии летят навстречу друг другу. В какую сторону они полетят после абсолютно неупругого столкновения? Удар лобовой.
46. Можно ли по графику зависимости пути от времени найти среднюю скорость движения м.т. по траектории?
47. Изменится ли ускорение машины, если она совершает крутой поворот с постоянной скоростью, по сравнению с ее ускорением на закруглении большего радиуса?
48. Чем отличается кинетическая энергия вращательного движения тела от кинетической энергии его поступательного движения?
49. Почему контактный провод трамвайной линии всегда идет зигзагом, а не параллельно рельсам?
50. Под каким углом разлетятся два одинаковых упругих шара после центрального удара, если один из них до удара покоился?
Контрольные вопросы
1. Дайте характеристику основных физических понятий кинематики.
2. Назовите четыре типа взаимодействий современной физики.
3. Чем характеризуется положение материальной точки в пространстве?
4. В чем различие вектора перемещения и расстояния, пройденного м.т. по траектории при ее движении?
5. Физический смысл мгновенной скорости. Как направлен вектор мгновенной скорости?
6. Физический смысл мгновенного ускорения. Как направлен вектор мгновенного ускорения?
7. Физический смысл нормального, тангенциального, полного ускорения. Как направлено каждое из них?
8. В чем заключается физический смысл угловой скорости?
9. Как связаны линейная и угловая скорости в векторном виде?
11. Что такое импульс м.т. (тела)?
12. Сформулируйте закон всемирного тяготения и его границы применения.
13. Преобразования Галилея и принцип относительности.
14. Принцип независимости действия сил.
16. Что такое кинетическая энергия и как она связана с работой?
17. Сформулируйте закон сохранения механической энергии.
18. Cформулируйте теорему Штейнера-Гюйгенса.
19. Сформулируйте закон сохранения вектора момента импульса.
20. Запишите формулу работы тел при вращательном движении.
© ФГОУ ВПО Красноярский государственный аграрный университет, 2015
Видео:Камень брошен горизонтально, надо искать радиус кривизны траектории. (Волькенштейн 1.20)Скачать

Цилиндр радиуса R, расположенный вертикально, вращается вокруг своей оси
Видео:Видеоурок по математике "Цилиндр"Скачать

Условие задачи:
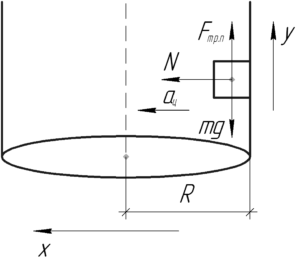
Цилиндр радиуса \(R\), расположенный вертикально, вращается вокруг своей оси с постоянной угловой скоростью \(\omega\). На внутренней поверхности цилиндра находится небольшое тело, вращающееся вместе с цилиндром. Коэффициент трения между телом и поверхностью цилиндра равен \(\mu\). При какой минимальной угловой скорости вращения цилиндра тело еще не будет скользить вниз по поверхности цилиндра?
Задача №2.4.41 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Видео:В горизонтальном цилиндрическом сосуде - Задача ЕГЭ по физике Часть 2Скачать

Решение задачи:
На рассматриваемое тело действуют 3 силы: сила тяжести \(mg\), сила трения покоя (именно покоя, так как тело не скользит вниз) \(F_ \) и сила реакции опоры \(N\). Первый закон Ньютона в проекции на ось \(y\) даст такое равенство:
Поскольку требуется найти минимальную угловую скорость, при которой тело не скользит, то в этом случае сила трения покоя должна принимать свое максимальное значение. Известно, что её можно посчитать по формуле (как и для силы трения скольжения):
Из второго закона Ньютона в проекции на ось \(x\) получим:
Запишем формулу определения центростремительного ускорения через угловую скорость \(\omega\) и радиус цилиндра \(R\):
Полученное выражение для силы реакции опоры \(N\) подставим в (1), тогда:
Задача решена в общем виде.
Видео:Линия пересечения двух поверхностей вращения (Метод вспомогательных сфер)Скачать

Ответ: \(\omega = \sqrt >>\).
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
📸 Видео
Цилиндр массой m = 1 кг и радиусом R = 4 см, на который намотана нерастяжимая невесомая нить - №Скачать

Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

Построение недостающих проекции сквозного отверстия в сфереСкачать

Почему площадь сферы в четыре раза больше её тени? [3Blue1Brown]Скачать
![Почему площадь сферы в четыре раза больше её тени? [3Blue1Brown]](https://i.ytimg.com/vi/JsrRqLK8zKg/0.jpg)
Как построить ЛИНИЮ ПЕРЕСЕЧЕНИЯ двух ЦИЛИНДРОВСкачать

9 класс, 41 урок, ЦилиндрСкачать

Радиус кривизны траекторииСкачать

Задача 27 Изотермическое сжатие газа в пятом отсеке горизонтального цилиндраСкачать

Цилиндр, вытянутый вдоль оси X. Урок 35.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать
Лекция 13. Пересечение поверхностей метод концентрических сферСкачать

Цилиндр и конус имеют общее основание и высоту. Высота цилиндра равна радиусу основания... (ЕГЭ)Скачать

ТЕМА 3. ПРИНЦИПЫ ПЕРЕСЕЧЕНИЯ ЦИЛИНДРА И ШАРА С ПРЯМЫМИ ПЛОСКОСТЯМИСкачать

Теплоизолированный цилиндр разделён подвижным теплопроводящим поршнем на две части. В одной - №29369Скачать

РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать

Лайфхаки ЕГЭ по математике: решения и ответы | Задание 8: цилиндр | Быстрая подготовка к ЕГЭСкачать

38. Построение линии пересечения горизонтально-проецирующего цилиндра вращения со сферойСкачать