График зависимости напряженности от радиуса цилиндра (8 видео)

Видео:Лекция 2-2 Потенциал - примерыСкачать

График зависимости напряженности от радиуса цилиндра

2017-05-27
В вакууме имеется скопление зарядов в форме длинного цилиндра радиуса $R_ = 2 см$ (рис.). Объемная плотность зарядов $\rho$ постоянна и равна $2 мкКл/м^ $. Найти напряженность поля в точках 1 и 2, лежащих на расстояниях $r_ = 1 см, r_ = 3 см$ от оси цилиндра, и разность потенциалов между этими точками. Построить графики $E_ (r)$ и $\phi(r)$.

Поле создано зарядом, равномерно распределенным по объему. Конфигурация зарядов позволяет считать, что поле обладает осевой симметрией: силовые линии — прямые и в любой плоскости, перпендикулярной оси цилиндра, радиальны. (Очевидно, что вблизи концов цилиндра и при очень больших $r$ силовые линии не будут радиальны.) Предполагаемая симметрия позволяет искать напряженность поля с помощью теоремы Гаусса. Вспомогательной поверхности следует придать форму, цилиндрической поверхности, коаксиальной заряду. Длина этого цилиндра может быть произвольной, но заведомо много меньше, чем длина-заряженного цилиндра, в противном случае предположение о плоскорадиальной структуре поля несправедливо.

Разность потенциалов можно найти, используя выражение напряженности поля как функции координат:

$\phi_ — \phi_ = \int_ ^ \vec d \vec = \int_ ^ \vec _ d \vec $. (1)

Очевидно, что разность потенциалов двух заданных точек не зависит от выбора начала отсчета потенциала. Однако по условию задачи требуется еще построить график зависимости $\phi(r)$. Для этого надо предварительно выбрать начало отсчета потенциала. Из приведенных выше соображений о симметрии поля ясно, что оно не может находиться в бесконечности.

По-видимому, характер функциональной зависимости $E(r)$ для точек, лежащих внутри и вне объемного заряда, различен. Поэтому следует провести две вспомогательные цилиндрические поверхности $S_ $ и $S_ $ с радиусами $r_ R_ $. Для каждой поверхности теорема Гаусса может быть записана в виде

Боковая поверхность вспомогательного цилиндра и его торцы находятся заведомо в разных условиях относительно силовых линий поля, причем во всех точках торцов $\hat , d \vec > = \pi /2$ и поток вектора напряженности сквозь торцовые поверхности равен нулю. На боковых поверхностях $S_ $ нормаль совпадает с направлением радиус-вектора, поэтому $\vec d \vec = E_ dS$ и

Все точки боковой поверхности находятся в одинаковых условиях относительно заряда, что позволяет считать $E_ $ постоянной величиной. Тогда

Читайте также: Сорвана свечная резьба цилиндра

$\int_ > E_ dS = E_ \int_ > E_ dS = E_ \cdot 2 \pi rh$, (3)

где $r$ и $h$ — радиус и высота вспомогательной поверхности.

Сумма зарядов, охваченных вспомогательной поверхностью, стоящая в правой части выражения (2), зависит от радиуса вспомогательной поверхности.

При $r R_ \sum Q = \rho \pi R_ ^ h$.

Подставляя это выражение в (2) и заменяя интеграл по замкнутой поверхности $S_ $ правой частью равенства (3), получаем

$E_ \cdot 2 \pi rh = \rho \pi R_ ^ h / \epsilon_ $,

$E_ = \rho R_ ^ / (2 \epsilon_ r)$. (6)

Подставляя в (5) $r = r_ $ и в (6) $r = r_ $, находим:

$E_ = 1,1 \cdot 10^ В/м ; E_ = 1,5 \cdot 10^ В/м$.

Для определения разности потенциалов между точками 1 и 2 по равенству (1) интеграл следует разбить на два: в пределах от точки 1 до поверхности, ограничивающей объемный заряд, и от этой поверхности до точки 2:

В первый интеграл следует подставлять выражение (5), во второй — выражение (6):

Для построения графика $E_ (r)$ на основании выражений (5) и (6) целесообразно сначала рассчитать $E_ $ при $r = R_ $:

$E(R_ ) = \rho R_ /(2 \epsilon_ ) = 2,3 \cdot 10^ В/м.$

Расчет по формулам (5) и (6) дает один и тот же результат, так как напряженность на этой поверхности не терпит разрыва.

Графическая зависимость $E_ (r)$ показана на рис..

График зависимости $\phi(r)$ можно построить из анализа графика $E_ (r)$, учитывая, что $E_ = — d \phi / dr$. Начало отсчета потенциала можно выбрать в любой точке области, где справедливы выражения (4) и (5). Выберем начало отсчета на оси объемного заряда: $\phi (0) = 0$. Так как во всей области $E_ > 0$, т. е. $(d \phi/dr) 0$], соответственно $(d^ \phi/ dr^ ) R_ E_ $ убывает [$(dE_ /dr) 0$ и график $\phi (r)$ обращен вогнутостью вверх. При $r = R_ $ кривая $\phi(r)$ имеет точку перегиба (вторая производная изменяет знак). График $\phi(r)$ изображен на риc.

Читайте также: Замена цилиндра в скутере

Если изменить начало отсчета потенциала, то характер графика не изменяется, например при выборе начала отсчета на поверхности объемного заряда [$\phi(R_ ) = 0$] график примет вид, изображенный на рис. пунктиром.

Видео:Урок 224. Напряженность поля неточечных зарядовСкачать

График зависимости напряженности от радиуса цилиндра

Продемонстрируем возможности теоремы Остроградского-Гаусса на нескольких примерах.

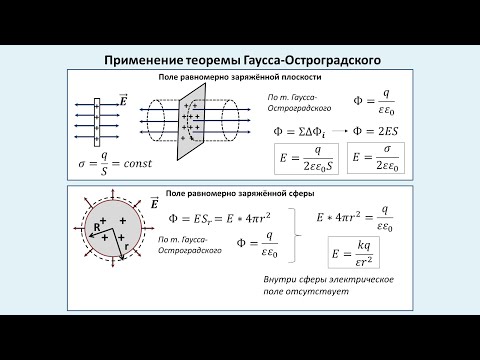
Поле бесконечной однородно заряженной плоскости

Поверхностная плотность заряда на произвольной плоскости площадью S определяется по формуле:

где d q – заряд, сосредоточенный на площади d S; d S – физически бесконечно малый участок поверхности.

Пусть σ во всех точках плоскости S одинакова. Заряд q – положительный. Напряженность во всех точках будет иметь направление, перпендикулярное плоскости S (рис. 2.11).

Очевидно, что в симметричных, относительно плоскости точках, напряженность будетодинакова по величине и противоположна по направлению.

Представим себе цилиндр с образующими, перпендикулярными плоскости, и основаниями ΔS, расположенными симметрично относительно плоскости (рис. 2.12).


Рис. 2.11	Рис. 2.12

Применим теорему Остроградского-Гаусса. Поток Ф_Е через боковую часть поверхности цилиндра равен нулю, т.к . Дляоснования цилиндра

Суммарный поток через замкнутую поверхность (цилиндр) будет равен:

Внутри поверхности заключен заряд . Следовательно, из теоремы Остроградского–Гаусса получим:

откуда видно, что напряженность поля плоскости S равна:

Полученный результат не зависит от длины цилиндра. Это значит, что на любом расстоянии от плоскости

Поле двух равномерно заряженных плоскостей

Пусть две бесконечные плоскости заряжены разноименными зарядами с одинаковой по величине плотностью σ (рис. 2.13).

Результирующее поле, как было сказано выше, находится как суперпозиция полей, создаваемых каждой из плоскостей .

Вне плоскостей напряженность поля

Полученный результат справедлив и для плоскостей конечных размеров, если расстояние между плоскостями гораздо меньше линейных размеров плоскостей (плоский конденсатор).

Между пластинами конденсатора действует сила взаимного притяжения (на единицу площади пластин):

Механические силы, действующие между заряженными телами, называют пондермоторными.

Тогда сила притяжения между пластинами конденсатора:

где S – площадь обкладок конденсатора. Т.к. , то

Это формула для расчета пондермоторной силы.

Поле заряженного бесконечно длинного цилиндра (нити)

Пусть поле создается бесконечной цилиндрической поверхностью радиуса R, заряженной с постоянной линейной плотностью , где d q – заряд, сосредоточенный на отрезке цилиндра (рис. 2.14).

Читайте также: Рабочий цилиндр сцепления поло седан 2012 артикул

Из соображения симметрии следует, что Е в любой точке будет направлена вдоль радиуса, перпендикулярно оси цилиндра.

Представим вокруг цилиндра (нити) коаксиальную замкнутую поверхность (цилиндр в цилиндре) радиуса r и длиной l (основания цилиндров перпендикулярно оси). Для оснований цилиндров для боковой поверхности т.е. зависит от расстояния r.

Следовательно, поток вектора через рассматриваемую поверхность, равен

При на поверхности будет заряд По теореме Остроградского-Гаусса , отсюда

Если , т.к. внутри замкнутой поверхности зарядов нет (рис.2.15).

Если уменьшать радиус цилиндра R (при ), то можно вблизи поверхности получить поле с очень большой напряженностью и, при , получить нить.

Поле двух коаксиальных цилиндров с одинаковой линейной плотностью λ, но разным знаком

Внутри меньшего и вне большего цилиндров поле будет отсутствовать (рис. 2.16) .

В зазоре между цилиндрами, поле определяется так же, как и в предыдущем случае:

Это справедливо и для бесконечно длинного цилиндра, и для цилиндров конечной длины, если зазор между цилиндрами намного меньше длины цилиндров (цилиндрический конденсатор).

Поле заряженного пустотелого шара

Пустотелый шар (или сфера) радиуса R заряжен положительным зарядом с поверхностной плотностью σ. Поле в данном случае будет центрально симметричным, – в любой точке проходит через центр шара. ,и силовые линии перпендикулярны поверхности в любой точке. Вообразим вокруг шара – сферу радиуса r (рис. 2.17).

Если то внутрь воображаемой сферы попадет весь заряд q, распределенный по сфере, тогда

Внутри сферы, при поле будет равно нулю, т.к. там нет зарядов: