Видео:Урок 218. Напряженность электрического поляСкачать

Графики зависимости напряженности поля цилиндра от расстояния
2017-05-27
В вакууме имеется скопление зарядов в форме длинного цилиндра радиуса $R_ = 2 см$ (рис.). Объемная плотность зарядов $\rho$ постоянна и равна $2 мкКл/м^ $. Найти напряженность поля в точках 1 и 2, лежащих на расстояниях $r_ = 1 см, r_ = 3 см$ от оси цилиндра, и разность потенциалов между этими точками. Построить графики $E_ (r)$ и $\phi(r)$.
Поле создано зарядом, равномерно распределенным по объему. Конфигурация зарядов позволяет считать, что поле обладает осевой симметрией: силовые линии — прямые и в любой плоскости, перпендикулярной оси цилиндра, радиальны. (Очевидно, что вблизи концов цилиндра и при очень больших $r$ силовые линии не будут радиальны.) Предполагаемая симметрия позволяет искать напряженность поля с помощью теоремы Гаусса. Вспомогательной поверхности следует придать форму, цилиндрической поверхности, коаксиальной заряду. Длина этого цилиндра может быть произвольной, но заведомо много меньше, чем длина-заряженного цилиндра, в противном случае предположение о плоскорадиальной структуре поля несправедливо.
Разность потенциалов можно найти, используя выражение напряженности поля как функции координат:
$\phi_ — \phi_ = \int_ ^ \vec d \vec = \int_ ^ \vec _ d \vec $. (1)
Очевидно, что разность потенциалов двух заданных точек не зависит от выбора начала отсчета потенциала. Однако по условию задачи требуется еще построить график зависимости $\phi(r)$. Для этого надо предварительно выбрать начало отсчета потенциала. Из приведенных выше соображений о симметрии поля ясно, что оно не может находиться в бесконечности.
По-видимому, характер функциональной зависимости $E(r)$ для точек, лежащих внутри и вне объемного заряда, различен. Поэтому следует провести две вспомогательные цилиндрические поверхности $S_ $ и $S_ $ с радиусами $r_ R_ $. Для каждой поверхности теорема Гаусса может быть записана в виде
Боковая поверхность вспомогательного цилиндра и его торцы находятся заведомо в разных условиях относительно силовых линий поля, причем во всех точках торцов $\hat , d \vec> = \pi /2$ и поток вектора напряженности сквозь торцовые поверхности равен нулю. На боковых поверхностях $S_ $ нормаль совпадает с направлением радиус-вектора, поэтому $\vec d \vec = E_ dS$ и
Все точки боковой поверхности находятся в одинаковых условиях относительно заряда, что позволяет считать $E_ $ постоянной величиной. Тогда
$\int_ > E_ dS = E_ \int_ > E_ dS = E_ \cdot 2 \pi rh$, (3)
где $r$ и $h$ — радиус и высота вспомогательной поверхности.
Сумма зарядов, охваченных вспомогательной поверхностью, стоящая в правой части выражения (2), зависит от радиуса вспомогательной поверхности.
При $r R_ \sum Q = \rho \pi R_ ^ h$.
Подставляя это выражение в (2) и заменяя интеграл по замкнутой поверхности $S_ $ правой частью равенства (3), получаем
$E_ \cdot 2 \pi rh = \rho \pi R_ ^ h / \epsilon_ $,
$E_ = \rho R_ ^ / (2 \epsilon_ r)$. (6)
Подставляя в (5) $r = r_ $ и в (6) $r = r_ $, находим:
$E_ = 1,1 \cdot 10^ В/м ; E_ = 1,5 \cdot 10^ В/м$.
Для определения разности потенциалов между точками 1 и 2 по равенству (1) интеграл следует разбить на два: в пределах от точки 1 до поверхности, ограничивающей объемный заряд, и от этой поверхности до точки 2:
В первый интеграл следует подставлять выражение (5), во второй — выражение (6):
Для построения графика $E_ (r)$ на основании выражений (5) и (6) целесообразно сначала рассчитать $E_ $ при $r = R_ $:
Читайте также: Прямоугольный параллелепипед описан около цилиндра равен 16 найти высоту цилиндра
$E(R_ ) = \rho R_ /(2 \epsilon_ ) = 2,3 \cdot 10^ В/м.$
Расчет по формулам (5) и (6) дает один и тот же результат, так как напряженность на этой поверхности не терпит разрыва.
Графическая зависимость $E_ (r)$ показана на рис..
График зависимости $\phi(r)$ можно построить из анализа графика $E_ (r)$, учитывая, что $E_ = — d \phi / dr$. Начало отсчета потенциала можно выбрать в любой точке области, где справедливы выражения (4) и (5). Выберем начало отсчета на оси объемного заряда: $\phi (0) = 0$. Так как во всей области $E_ > 0$, т. е. $(d \phi/dr) 0$], соответственно $(d^ \phi/ dr^ ) R_ E_ $ убывает [$(dE_ /dr) 0$ и график $\phi (r)$ обращен вогнутостью вверх. При $r = R_ $ кривая $\phi(r)$ имеет точку перегиба (вторая производная изменяет знак). График $\phi(r)$ изображен на риc.
Если изменить начало отсчета потенциала, то характер графика не изменяется, например при выборе начала отсчета на поверхности объемного заряда [$\phi(R_ ) = 0$] график примет вид, изображенный на рис. пунктиром.
Видео:Урок 224. Напряженность поля неточечных зарядовСкачать

Графики зависимости напряженности поля цилиндра от расстояния
Рассмотрим несколько примеров вычисления разности потенциалов между точками поля, созданного некоторыми заряженными телами.
Разность потенциалов между точками поля, образованного двумя бесконечными заряженными плоскостями
Мы показали, что напряженность связана с потенциалом
где – напряженность электростатического поля между заряженными плоскостями, найденная в п. 2.5.2 с помощью теоремы Остроградского–Гаусса; σ = q/S– поверхностная плотность заряда.
Теперь, чтобы получить выражение для потенциала между плоскостями, проинтегрируем выражение (3.7.1):
На рисунке 3.5 изображена графическая зависимость напряженности E и потенциала φ от расстояния между плоскостями.
Разность потенциалов между точками поля,образованного бесконечно длинной цилиндрической поверхностью
В п. 2.5 с помощью теоремы Остроградского-Гаусса мы показали, что, т.к. , то (см. рис. 3.6)
Т.к. то , отсюда найдем разность потенциалов в произвольных точках 1 и 2:
На рисунке 3.6 изображена зависимость напряженности E и потенциала от r. (Здесь и далее E – изображена сплошной линией, а – пунктирной).
Разность потенциалов между обкладками цилиндрического конденсатора
В п. 2.5. мы нашли, что (рис. 3.7)
Отсюда так же, как и в предыдущем случае, разность потенциалов будет равна:
Таким образом, внутри меньшего цилиндра имеем , Е = 0, между обкладками потенциал уменьшается по логарифмическому закону, а вторая обкладка (вне цилиндров) экранирует электрическое поле и φ и Е равны нулю.
На рисунке 3.7 изображена зависимость напряженности E и потенциала от r.
Разность потенциалов между точками поля, образованного заряженной сферой (пустотелой)
Напряженность поля сферы (рис. 3.8) определяется формулой: .
Разность потенциалов внутри диэлектрического заряженного шара
Имеем диэлектрический шар (рис. 3.9), заряженный с объемной плотностью
В п. 2.5 с помощью теоремы Остроградского–Гаусса мы нашли, что внутри шара .
Теперь найдем разность потенциалов внутри шара:
Отсюда находим потенциал шара:
Из полученных соотношений можно сделать следующие выводы.
С помощью теоремы Гаусса сравнительно просто можно рассчитать Е и φ от различных заряженных поверхностей.
Напряженность поля в вакууме изменяется скачком при переходе через заряженную поверхность.
Потенциал поля – всегда непрерывная функция координат.
Видео:Лекция 2-2 Потенциал - примерыСкачать

Построение графика зависимости напряженности электрического поля от расстояния для тел сферической формы
Цели урока:
- Образовательные:
- продолжить формирование представлений и знаний о напряженности электрического поля;
- научить анализировать условие задачи и прогнозировать вид графической зависимости;
- научить применять изученные закономерности в измененной ситуации;
- выработать умение самостоятельно применять знания в комплексе (информатика и физика);
- развить навыки построения графиков функции;
- совершенствование навыков решения физических задач с помощью компьютерных технологий;
- воспитание культуры умственного труда;
- создание положительной мотивации к учебе.
Читайте также: Главный цилиндр тормоза ваз 2105
Средства обучения: компьютеры, мультимедийный проектор, экран, учебник «Физика» 10класс, автор В.А.Касьянов, М.:Дрофа, 2002.
Тип урока: урок комплексного применения знаний.
Методы обучения: словесный, наглядный, исследовательский, практический.
Аннотация урока
Урок решения задач с построением графиков зависимости напряженности от расстояния проводится после изучения тем: «Принцип суперпозиции полей», «Проводники и диэлектрики в электрическом поле» с тем, чтобы можно было охватить варианты задач, содержащие в себе смешанные среды (проводники, диэлектрики). Тогда графики получаются более наглядными и легко проследить различия между величиной напряженности поля в различных средах.
Задачи на построение графиков функций нередко вызывают затруднения у учащихся ввиду большого количества обрабатываемых числовых данных. Использование компьютерных прикладных программ (Excel) упрощает построение геометрически сложных графиков и позволяет делать это с заданным интервалом изменяющейся величины. При внесении поправок в числовые данные результат оперативно отображается на мониторе, что позволяет наглядно анализировать построение. При решении разных задач результаты легко сравниваются. Использование мультимедийного проектора позволяет быстро вывести результат на экран , после чего можно приступить к коллективному обсуждению. Интеграция традиционного обучения и инновационных технологий при изучении этой темы дает устойчивый положительный результат. Урок проводится в компьютерном классе.Использованная литература:
1. Физика в 10 классе. Модели уроков. Ю.А.Сауров. – Москва: Просвещение, 2005. – стр.183-194.
2. Физика.Задачник.9-11 кл. Гольдфарб Н.И. – Москва.:Дрофа,1998. – стр.87-88.
3. Сборник задач по общему курсу физики. Волькенштейн В.С. – Санкт-Петербург.: «Специальная литература», 1997. – стр.106.
4. Электронный учебник «Открытая физика» часть 2, под редакцией С.М.Козела.Этапы урока Время, мин Приемы и методы Организационный момент 1 Актуализация знаний. Повторение. 7 Фронтальный опрос. Постановка учебной проблемы. Решение задачи. 7 Объяснение учителя. Медиапроектор. Формирование умений. Коллективное решение задач. 15 Работа учащихся за компьютером. Физкультминутка для глаз. 2 Совершенствование знаний и умений. Анализ решенных задач. 10 Выступление учащихся. Оценка знаний . Подведение итогов 3 Выделение главного. Сообщение учителя. Обсуждаются вопросы: (на экране слайды, материал которых ученики могут использовать в ответе)
1. В чем состоит принцип суперпозиции полей?
2. Как ведет себя проводник в электростатическом поле? Что можно сказать о поле внутри проводника?
3. Существует ли электрическое поле внутри диэлектрика при отсутствии внешнего поля; при наличии внешнего поля?
4. В чем различие процессов, происходящих в проводнике и диэлектрике, помещенных в электрическое поле?
5. По какой формуле можно рассчитать напряженность поля, образованного заряженным металлическим шаром?
6. Как найти напряженность поля внутри слоя диэлектрика?Рассмотрим следующую задачу: (Выведена на экран с помощью мультимедийного проектора).
Металлический заряженный шар помещен в центре толстого сферического слоя , изготовленного из металла. Начертите график зависимости напряженности поля от расстояния от центра сферы.
Как вам известно, внутри заряженного шара напряженность электрического поля равна нулю. Поэтому на участке от 0 до R график представляет собой линию, совпадающую с осью r (график «лежит» на оси).
На поверхности шара напряженность поля равна (на графике видно возрастание величины напряженности Е при r = R).
При изменении r от R до R1 и от R2 до бесконечности значение Е убывает по закону: (график-гипербола).
«Провал» графика на участке от R1 до R2 показывает убывание напряженности до нуля внутри металлического слоя.
Таким образом, на экране мы видим примерный график зависимости напряженности поля от расстояния r.
Теперь решим две задачи (по вариантам) и построим графики зависимости Е(r) с использованием компьютерной программы Excel, после чего мы сможем сравнить графики и проанализировать полученные результаты. Условия задачи вы видите на экране. При построении электронной таблицы шаг построения графика считать 5 см. (Условия задач выведены на экран с помощью мультимедийного проектора).
Читайте также: Подставка для цилиндра снеллена
Задача 2 (для 1 варианта)
Металлический шар радиусом 20 см, имеющий заряд 10 нКл, помещен в центре сферического слоя внутренним радиусом 50 см и внешним радиусом 80 см, изготовленным из диэлектрика проницаемостью, равной 2. Начертите график зависимости напряженности поля от расстояния от центра сферы.
Задача 3 (для 2 варианта)
Заряд Q = 20 нКл равномерно распределен по объему шара радиусом 30 см , изготовленным из непроводящего материала с проницаемостью, равной 2,5. Шар помещен в центре толстого сферического металлического слоя толщиной 50 см. Воздушный промежуток между шаром и сферой имеет толщину 25 см. Начертите график зависимости напряженности поля от расстояния от центра сферы.
Учащиеся приступают к работе на компьютере (15 мин.)
Результаты решения задач (оба варианта) выводятся на экран (мультимедийный проектор).
В это время учащиеся выполняют расслабляющую гимнастику для глаз.Ученики у экрана объясняют решение задачи и описывают полученный график.
Приступим к анализу полученных графиков.
1. Как зависит величина напряженности от расстояния на каждом участке графика?
2. На каких участках графики различаются и почему?
3. Чем объясняются «провалы» графиков при значении r от 0,5 до 0,8 м? Почему они имеют разный вид?
4. Какая величина в условии 2 задачи обуславливает «глубину провала»?
5. Как будет изменяться вид графиков при уменьшении (увеличении) величины электрического заряда?
6. Как будет изменяться вид графиков при с уменьшением (увеличением) геометрических размеров шара, толщины слоя?
7. Почему функция Е имеет в некоторых точках два значения?
8. Каковы особенности использования программы Excel в условиях данной задачи?
9. Почему таблица значений имеет «многоступенчатый» вид?
10. Какие затруднения вызвало у вас решение задачи?Результат решения задачи 2, полученный учащимися 1 варианта.
r 0 0,05 0,1 0,15 0,2 0,25 0,3 0,35 0,4 0,45 0,5 0,55 0,6 0,65 0,7 0,75 0,8 0,85 0,9 0,95 1 Е 0 0 0 0 0 Е 2250 1440 1000 734,69 562,5 444,44 360 140,62 124,56 111,11 99,72 90 Е 180 149 125 107 92 80 70 Результат решения задачи 3, полученный учащимися 2 варианта.
r 0 0,05 0,1 0,15 0,2 0,25 0,3 0,35 0,4 0,45 0,5 0,55 0,6 0,65 0,7 0,75 0,8 0,85 0,9 0,95 1 Е 0 133,3 266,6 399,9 533,2 Е 4500 2880 2000 1469,38 1125 888,88 720 281,25 249,13 222,22 199,44 180 Е 0 0 0 0 0 0 0 Подведем итог:
Решение задач на построение графиков зависимости Е (r) позволяет наглядно представить геометрию электрического
поля и точнее описать его. Интересно также проводить виртуальные эксперименты с внесением в электрическое поле разнородных тел и наблюдать за изменением картины поля в этих случаях.Домашнее задание
1. Ответить на вопрос: В чем наблюдается различие: проводник и диэлектрик помещены в электрическое поле и разрезаны пополам; вынесены из поля?
2. Составить и решить задачу, аналогичную решенной в классе с измененными условиями. Результат сдать учителю
в распечатанном виде.Методические рекомендации:
1. На оси r нельзя отобразить два значения одного аргумента, график в этом случае искажается (« растягивается» по горизонтали и «ложится», см. график ниже),поэтому нужно составлять не одну таблицу, а отдельную для каждого участка графика, описываемого отдельной функцией Е(r).
2. При задании функции в таблице знаменатель нужно заключать в скобки.🎦 Видео
НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ суперпозиция полейСкачать
Задача №2. Потенциал проводящей сферы.Скачать
Лекция 1-4 Теорема Гаусса Формулировка и примерыСкачать
Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать
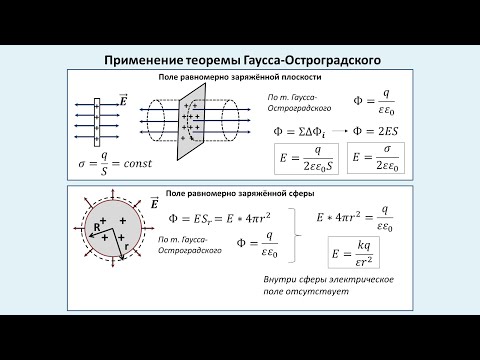
Применение теоремы Гаусса-Остроградского. Напряжённость поля пластины, сферы и шара.Скачать
Урок 222. Поток вектора напряженности электрического поляСкачать
Электрическое поле. Напряженность электрического поля. Силовые линии электрического поля. 10 класс.Скачать
Физика 10 класс. Поле равномерно заряженной сферыСкачать
3.9Скачать
43. Применение теоремы ГауссаСкачать
Поле заряженного кольцаСкачать
Билет №02 "Теорема Гаусса"Скачать
Урок 223. Теорема ГауссаСкачать
Студенты российского вуза разработали вечный двигатель #вечныйдвигатель #изобретенияСкачать
Продолжаем говорить о напряженности⚡🔥#физикаСкачать
Электромагнетизм Пр3.4. Теорема Гаусса. Поле бесконечного цилиндра.Скачать
Силовые линии электрического поляСкачать