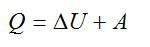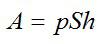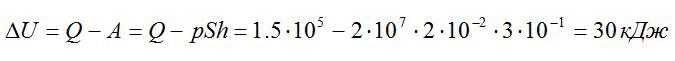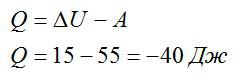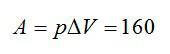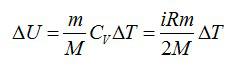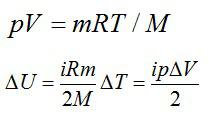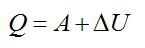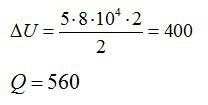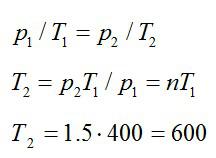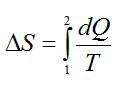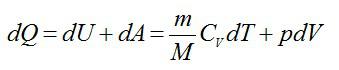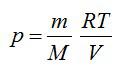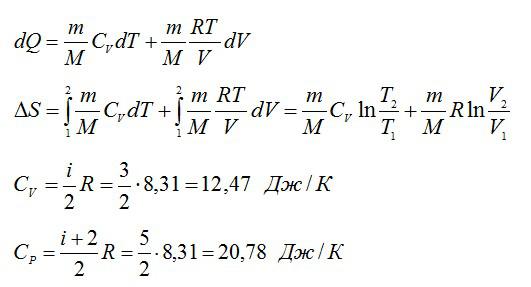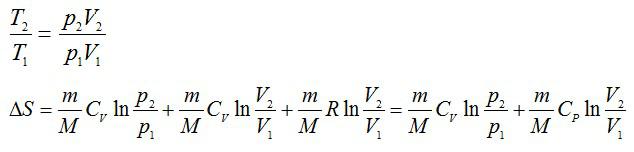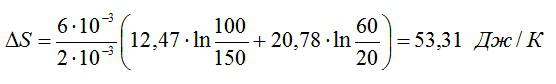Идеальному газу находящемуся в цилиндре с поршнем сообщили количество теплоты

Первый закон, или первое начало термодинамики является частным случаем закона сохранения энергии. Разберемся, как он работает, с помощью решения простых задач. Кстати, у нас есть и примеры решения задач на второе начало термодинамики.

Подписывайтесь на наш телеграм-канал, чтобы не только легко решать задачи, но и узнавать лайфхаки для любых жизненных ситуаций.

Первый закон термодинамики: решение задач

Алгоритм решения задач на первый закон термодинамики ничем не отличается от алгоритма решения любой другой физической задачи. С ним вы можете ознакомиться, открыв нашу универсальную памятку. Также полезно будет держать под рукой формулы, которые часто используются при решении задач.

Задача №1. Применение первого закона термодинамики

Газ находился в цилиндре с поршнем площадью поперечного сечения 200 см^2. После того, как газ нагрели, сообщив ему количество теплоты в 1,5*10^5 Дж, поршень сдвинулся на расстояние h=30 см. Как изменилась внутренняя энергия газа, если его давление осталось равным 2*10^7 Па.

Запишем первое начало термодинамики:

Работу против внешних сил, которую совершил газ, можно найти по формуле из механики:

Ответ: 30 кДж.

Задача №2. Применение первого закона термодинамики

Над газом была совершена работа 55 Дж, а его внутренняя энергия увеличилась на 15 Джоулей. Какое количество теплоты получил или отдал газ в этом процессе?

Записываем первое начало термодинамики и подставляем значения:

A пишется со знаком «минус», так как это работа внешних сил над газом, а не наоборот.

Ответ: в процессе газ отдал 40 Дж теплоты.

Задача №3. Расчет работы, изменения внутренней энергии и количества теплоты

Кислород нагрели при постоянном давлении p=80 кПа. Объем газа увеличился с 1 до 3 кубических метров. Определить изменение внутренней энергии кислорода, работу, совершенную газом, и количество теплоты, сообщенное ему.

Изменение внутренней энергии равно:

Используем уравнение состояния газа:

Число степеней свободы i для двухатомной молекулы равно 5.

Согласно первому закону термодинамики, сообщенное газу тепло равно:

Ответ: А=160 кДж, ∆U=400 кДж, Q=560 кДж.

Задача №4. Изопроцессы

Газ находится в баллоне при температуре 400 К. До какой температуры нужно нагреть газ, чтобы его давление увеличилось в 1,5 раза?

Читайте также: Рабочий цилиндр сцепления блейзер шевроле

Так как нагревание газа происходит при постоянном объеме, процесс – изохорный. При изохорном процессе:

Ответ: 600 К.

Задача №5. Расчет изменения энтропии

Найти изменение ∆S энтропии при расширении массы m = 6 г гелия от объема V1 = 20 л под давлением р1 = 150 кПа к объему V2 = 60 л под давлением р2 = 100 кПа.

Изменение энтропии при переходе вещества из состояния 1 в состояние 2:

Согласно первому началу термодинамики:

Из уравнения Менделеева-Клапейрона выразим давление:

Из уравнения Менделеева-Клапейрона:

Кстати! Для наших читателей действует скидка 10% на любой вид работы.

Вопросы по теме «1-ый закон термодинамики»

Вопрос 1. Приведите пример действия первого закона термодинамики.

Ответ. В качестве примера можно привести газ в сосуде. Если сообщить ему какое-то количество теплоты, оно пойдет на увеличение внутренней энергии газа в сосуде.

Вопрос 2. Сформулируйте первый закон термодинамики.

Ответ. В любой изолированной системе запас энергии остается постоянным.

Вопрос 3. Как еще можно сформулировать первый закон термодинамики?

Ответ. Вот разные формулировки первого закона термодинамики:

1. Количество теплоты, полученное системой, идет на изменение внутренней энергии системы, а также на совершение работы против внешних сил.
2. Невозможен вечный двигатель первого рода (двигатель, совершающий работу без затраты энергии).

Вопрос 4. Что такое изопроцесс? Какие есть изопроцессы?

Изопроцесс – это термодинамический процесс, при котором один из параметров системы (давление, объем, температура, энтропия) остается неизменным.

• изотермическим (T=const);
• изобарным (P=const);
• изохорным (V=const);
• Адиабатическим (отсутствует теплообмен с окружающей средой).

Вопрос 5. При каком изопроцессе газ не совершает работу?

Ответ. При изохорном.

Ищете, где почитать теорию по теме, а учебника нет под рукой? Далеко ходить на надо, почитайте наш отдельный материал по первому началу термодинамики. А если при решении заданий понадобится помощь, обращайтесь в профессиональный студенческий сервис.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Идеальному газу находящемуся в цилиндре с поршнем сообщили количество теплоты

Систему отсчета, связанную с Землей, будем считать инерциальной. В процессе медленного подъема поршня его ускорение считаем ничтожно малым. Поэтому сумма приложенных к поршню сил при его движении равна нулю. В проекциях на вертикальную ось у получаем: \( — — Mg = 0 \), или \(

Отсюда получаем давление газа \( p \), под движущимся поршнем: \(

+ \frac > \). Используем модель одноатомного идеального газа: \( \left\ pV = vRT\\ U = \frac vRT \end \right. \)

Читайте также: Камминз зазор поршень цилиндр

Отсюда получаем: \( U = \frac pV \)

Внутренняя энергия газа в исходном состоянии \( = \frac

Sh \), а в конечном состоянии

Процесс движения поршня идет при постоянном давлении газа \(

\) Поэтому из первого начала термодинамики получаем: \( Q = — +

Подставляя сюда выражения для \(

\), \( \) и \( \), получим: \( Q = \frac (

S + Mg)(H — h) = \) \( \frac Mgh + \frac (Mg +

Ответ: \( \frac Mgh + \frac (Mg +

Идеальному газу находящемуся в цилиндре с поршнем сообщили количество теплоты

В гладком вертикальном цилиндре под подвижным поршнем массой M = 5 кг и площадью S = 100 см 2 находится идеальный одноатомный газ. После сообщения газу некоторого количества теплоты поршень приподнялся на высоту Δh = 5 см над дном цилиндра, а газ нагрелся на ΔT = 30 К. Найдите удельную теплоёмкость газа в данном процессе. Давление в окружающей цилиндр среде равно p₀ = 10 4 Па, масса газа в цилиндре m = 0,12 г.

Как следует из условия, объём газа равен а давление равно в течение всего процесса подвода теплоты. Согласно уравнению Клапейрона — Менделеева где — количество газа (в молях). Отсюда В процессе подвода теплоты в изобарическом процессе будет выполняться соотношение: так что После сообщения газу некоторого количества теплоты температура газа увеличилась на а поршень приподнялся на высоту причём согласно первому началу термодинамики где изменение внутренней энергии для одноатомного идеального газа а работа газа в изобарическом процессе

Таким образом, а удельная теплоёмкость газа в данном изобарическом процессе равна по определению:

I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом ((в данном случае — определение удельной теплоёмкости, уравнение Клапейрона—Менделеева, первое начало термодинамики, выражения для внутренней энергии идеального одноатомного газа и для работы газа при изобарическом процессе);

II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, и обозначений величин, используемых в условии задачи);

III) проведены необходимые математические преобразования, приводящие к правильному ответу;

Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют.

Лишние записи, не входящие в решение (возможно, неверные), не отделены от решения (не зачёркнуты, не заключены в скобки, рамку и т. п.).

В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) преобразования/вычисления не доведены до конца.

Представлены только положения и формулы, выражающие физические законы, применение которых необходимо для решения задачи, без каких-либо преобразований с их использованием, направленных на решение задачи, и ответа.

В решении отсутствует одна из исходных формул, необходимая для решения задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.

Количество теплоты переданное газу равна изменению внутренней энергии + работе газа+работе силы тяжести. При сложении работы газа и внутренней энергии получаем 5/2, но у вас 5/2 умножается еще и на работу силы тяжести. Я думаю 5/2 должно быть внутри скобки перед роS

Смотрите решение. То, про что Вы говорите, это не работа силы тяжести.

Идеальному газу находящемуся в цилиндре с поршнем сообщили количество теплоты

Систему отсчета, связанную с Землей, будем считать инерциальной. В процессе медленного подъема поршня его ускорение считаем ничтожно малым. Поэтому сумма приложенных к поршню сил при его движении равна нулю. В проекциях на вертикальную ось у получаем: \( — — Mg = 0 \), или \(

Отсюда получаем давление газа \( p \), под движущимся поршнем: \(

+ \frac > \). Используем модель одноатомного идеального газа: \( \left\ pV = vRT\\ U = \frac vRT \end \right. \)

Отсюда получаем: \( U = \frac pV \)

Внутренняя энергия газа в исходном состоянии \( = \frac

Sh \), а в конечном состоянии

Процесс движения поршня идет при постоянном давлении газа \(

\) Поэтому из первого начала термодинамики получаем: \( Q = — +

Подставляя сюда выражения для \(

\), \( \) и \( \), получим: \( Q = \frac (

S + Mg)(H — h) = \) \( \frac Mgh + \frac (Mg +

Ответ: \( \frac Mgh + \frac (Mg +