Имеет ли цилиндр ось симметрии если да то сколько (5 видео)

Некоторые фигуры, к примеру, разносторонние треугольники или отличные от прямоугольника параллелограммы оси симметрии не имеют. У других их может быть 1, 2, 4 или даже бесконечное множество.

Содержание

Есть ли ось симметрии у цилиндра
Порядок оси симметрии цилиндра
Плоскости симметрии
Имеет ли цилиндр ось симметрии если да то сколько
Что такое цилиндр: определение, элементы, виды, варианты сечения
Определение цилиндра
Основные элементы цилиндра
Урок геометрии в 11-м классе по теме «Цилиндр и конус»
Осевая и центральная симметрия
Что такое симметрия
Осевая симметрия
Центральная симметрия
Задачи на самопроверку
📽️ Видео

Видео:Центральная симметрия. 6 класс.Скачать

Есть ли ось симметрии у цилиндра

Основными элементами цилиндра являются два круга и все отрезки, соединяющие их окружности. Круги у цилиндров называются основаниями, а отрезки — образующими.

Ось симметрии разделяет фигуру на две зеркально идентичные части. То есть в симметричных фигурах у каждой точки есть симметричная относительно этой оси точка, принадлежащая этой же фигуре.

Цилиндр является телом вращения. То есть образуется он при вращении прямоугольника вокруг одной из своих сторон. С этой стороной и совпадает ось симметрии цилиндра, которая у этой фигуры имеется только одна.

У прямого цилиндра ось симметрии проходит через центры оснований. При этом ее длина равна высоте самой фигуры. Параллельное оси симметрии сечение цилиндра представляет собой прямоугольник, перпендикулярное — круг.

Видео:Осевая симметрия. 6 класс.Скачать

Порядок оси симметрии цилиндра

В геометрических фигурах могут присутствовать оси симметрии любых порядков — от первого и до бесконечного. Фигуры с осью второго порядка при повороте вокруг нее, к примеру, совмещаются сами с собой дважды, включая исходное положение. Такими свойствами отличаются правильные пирамиды и призмы с четным числом граней, а также прямоугольные параллелепипеды.

Цилиндр совпадет с собой при повороте на любой угол. Поэтому считается, что такая фигура имеет ось вращения бесконечного порядка.

Видео:Ось симметрииСкачать

Плоскости симметрии

Помимо оси, цилиндр имеет и плоскости симметрии. Такие плоскости зеркально отражают вторую половину фигуры, достраивая ее как целое. Одна из плоскостей симметрии у цилиндров проходит через центр перпендикулярно оси вращения.

Также плоскостями симметрии таких фигур являются все плоскости, содержащие ось их симметрии. Основания у цилиндров представляют собой круги. Осей же симметрии у окружностей имеется множество. Соответственно, и сам цилиндр будет иметь бесконечное множество плоскостей симметрии, совпадающих с осью его вращения.

Видео:Ось симметрии. Что это такое и как её проводить?Скачать

Имеет ли цилиндр ось симметрии если да то сколько

Ц илиндр, получается в результате вращения прямоугольника вокруг одной из его сторон.

Цилиндр состоит из двух кругов и множества отрезков .
Цилиндр – это геометрическое тело, состоящее из двух равных кругов, расположенных в параллельных плоскостях и множества отрезков, соединяющих соответственные точки этих кругов.
Определения элементов цилиндра :

Основания цилиндра – равные круги, расположенные в параллельных плоскостях

Высота цилиндра — это расстояние между плоскостями его оснований.

Ось цилиндра – это прямая, проходящая через центры основания цилиндра (ось цилиндра является осью вращения цилиндра).

Осевое сечение цилиндра – сечение цилиндра плоскостью, проходящей через ось цилиндра (осевое сечение цилиндра является плоскостью симметрии цилиндра). Все осевые сечения цилиндра – равные прямоугольники

Образующая цилиндра — это отрезок соединяющий точку окружности верхнего основания с соответственной точкой окружности нижнего основания. Все образующие параллельны оси вращения и имеют одинаковую длину, равную высоте цилиндра.

Образующая цилиндра при вращении вокруг оси образует боковую (цилиндрическую) поверхность цилиндра .

Радиус цилиндра – это радиус его основания.

Прямой цилиндр – это цилиндр, образующие которого перпендикулярны основанию.

Равновеликий цилиндр – цилиндр, у которого высота равна диаметру (показать равновеликий цилиндр: кнопкой со значком руки перевести модель обратно в интерактивный режим и изменить значение высоты и радиуса у предложенной модели так, чтобы ).

Разверткой боковой поверхности цилиндра является прямоугольник со сторонами H и C , где H – высота цилиндра, а C – длина окружности основания. Получим формулы для вычисления площадей боковой S _б и полной S _п поверхностей: S _б = H · C = 2π RH , S _п = S _б + 2 S = 2π R ( R + H ).

Читайте также: Ремкомплект главного тормозного цилиндра логан без абс

Задача № 1. Вычислить площадь боковой и полной поверхности цилиндра, у которого радиус равен 3 см, а высота 5 см (число пи и ответ округлить до целых).

2. Высота цилиндра равна h , радиус основания R . Найти площадь сечения плоскостью, проведенной параллельно оси цилиндра на, расстоянии a от нее.

Домашнее задание: 522, 524, 526.

Р.S/ кому интересно попрбуйте пройти по ссылке и посмотреть электронный ресурс про цилиндр

для начала на странице установите у себя на ПК модуль ОМS и закачайте модуль. На выскочившей таблице кликните воспроизвести. А дальше по порядку просмотрите все странички.
ВСЕМ СПАСИБО.

Видео:8 класс, 9 урок, Осевая и центральная симметрияСкачать

Что такое цилиндр: определение, элементы, виды, варианты сечения

В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения одной из самых распространенных трехмерных геометрических фигур – цилиндра. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Видео:№417. Сколько осей симметрии имеет: а) отрезок; б) прямая; в) луч?Скачать

Определение цилиндра

Далее мы подробно остановимся на прямом круговом цилиндре как самой популярной разновидности фигуры. Другие ее виды будут перечислены в последнем разделе данной публикации.

Прямой круговой цилиндр – это геометрическая фигура в пространстве, полученная путем вращения прямоугольника вокруг своей стороны или оси симметрии. Поэтому такой цилиндр иногда называют цилиндром вращения.

Цилиндр на рисунке выше получен в результате вращения прямоугольного треугольника ABCD вокруг оси O₁O₂ на 180° или прямоугольников ABO₂O₁/O₁O₂CD вокруг стороны O₁O₂ на 360°.

Видео:6 класс, 26 урок, СимметрияСкачать

Основные элементы цилиндра

Основания цилиндра – два одинаковых по размеру/площади круга с центрами в точках O₁ и O₂.
R – радиус оснований цилиндра, отрезки AD и BC – диаметры (d).
O₁O₂ – ось симметрии цилиндра, одновременно является его высотой (h).
l (AB, CD) – образующие цилиндра и одновременно с этим стороны прямоугольника ABCD. Равны высоте фигуры.

Развёртка цилиндра – боковая (цилиндрическая) поверхность фигуры, развернутая в плоскость; является прямоугольником.

длина данного прямоугольника равна длине окружности основания цилиндра ( 2πR );
ширина равна высоте/образующей цилиндра.

Примечание: формулы для нахождения площади поверхности и объема цилиндра представлены в отдельных публикациях.

Видео:Осевая и центральная симметрия, 6 классСкачать

Урок геометрии в 11-м классе по теме «Цилиндр и конус»

Сформировать навык решения задач по нахождению площади поверхности цилиндра, конуса, усеченного конуса.
Закрепить решение несложных задач и вопросы теории.

Оборудование и материалы: компьютер, мультимедиа проектор, раздаточный материал (модели цилиндра, конуса, усеченного конуса), бланки с математическим диктантом, линейка, карандаш, презентация “Цилиндр”, “Конус”.

Историческая справка.
Презентация.
Практическая работа.
Математический диктант.
Подведение итогов.
Задание на дом.

I этап. Организационный момент

Учитель: Тема нашего урока “Цилиндр и конус”. Для того чтобы наш урок прошел интересно, наглядно, теорию мы повторим с помощью презентации.

II этап. Историческая справка

Слово цилиндр происходит от греческого слова , что означает “валик”, “каток”. Конус в переводе с греческого “konos” означает “сосновая шишка”. С конусом и цилиндром люди знакомы с глубокой древности. В 1906 году была обнаружена книга Архимеда (287–212 гг. до н.э.) “О методе”, в которой дается решение задачи об объеме общей части пересекающихся цилиндров. Архимед приписывает честь открытия этого принципа – Демокриту (470–380 гг. до н.э.) – древнегреческому философу-материалисту. С помощью этого принципа Демокрит получил формулу для вычисления объема пирамиды и конуса.

Много сделала для геометрии школа Платона (428–348 гг. до н.э.). Платон был учеником Сократа (470–399 гг. до н.э.). Он в 387 г. до н.э. основал в Африке Академию, в которой работал 20 лет. Каждый, входящий в Академию, читал надпись: “Пусть сюда не входит никто, не знающий геометрии”. Школе Платона с частности принадлежит: а) исследование свойств призмы, пирамиды, цилиндра и конуса; б) изучение конических сечений.

Большой трактат о конических сечениях был написан Аполлонием Пергским (260–170 гг. до н.э.) – учеником Евклида (III в. до н.э.), который создал великий труд из 15 книг под названием “Начала”. Эти книги издаются и по сей день, а в школах Англии по ним учатся до сих пор.

Читайте также: Герметик для прокладки блока цилиндров

Учитель: Ученик № 1 расскажет нам все о цилиндре с помощью презентации “Цилиндр”.

Учитель: Ученик № 2 и помощью презентации “Конус” расскажет нам все о конусе. Все что вам необходимо, записывайте в тетрадь.

IV этап. Практическая работа

Учитель: Работа в парах. У вас на столе модели цилиндра, конуса, усеченного конуса. Сделав необходимые измерения, вычислите площади полных поверхностей этих фигур.

Ученики № 3, № 4, № 5 идут к доске и показывают свое решение.

V этап. Математический диктант

Учитель: Математический диктант (под копирку).

Математический диктант № 3 “Цилиндр, конус”

Какая фигура получается в сечении цилиндра плоскостью, проходящей:
а) через ось цилиндра, б) перпендикулярно к оси цилиндра?
Равны ли друг другу углы между образующими конуса и:
а) плоскостью основания; б) его осью?
Осевой сечение конуса представляет собой равносторонний треугольник со стороной а.Найдите высоту.
Высота и радиус основания конус равны 2 см. Через две образующие, угол между которыми равен 30 ° , проведена секущая плоскость. Найдите площадь сечения.
Как изменится площадь боковой поверхности конуса, если его образующую и радиус основания увеличить в 3 раза?
Сколько плоскостей симметрии имеет конус?

Какая фигура получается в сечении конуса плоскостью, проходящей: а) через ось конуса, б) перпендикулярно к оси конуса?
Что представляет собой сечение конуса плоскостью, проходящей через его вершину?
Осевое сечение цилиндра – квадрат, диагональ которого равна а. Найдите высоту цилиндра.
Высота конуса равна 2 см, а угол при вершине осевого сечения равен 120 ° . Найдите площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми равен 90 ° .
Как изменится площадь боковой поверхности конуса, если его образующую и радиус основания уменьшить в 2 раза?
Сколько осей симметрии имеет усеченный конус?

Ребят сдают работы. На экране высвечиваются правильные ответы. Учащиеся проверяют на оставшихся листах ответы (слайд 1).

VI этап. Подведение итогов.

Учитель сообщает результаты диктанта

Оценка “5” – все выполнено верно.

Оценка “4” – допущено не больше одной ошибки.

Оценка “3” – допущено не боле двух ошибок.

Оценка “2” – допущено больше трех ошибок.

Дается задача № 555 “Геометрия 10–11” (авторы Л.С. Атанасян и др.) (слайд 2).

Видео:Сколько осей симметрии имеет каждая фигура пентамино ➄ На уроках геометрииСкачать

Осевая и центральная симметрия

Видео:Построение цилиндра через ось симметрии:-)Скачать

Что такое симметрия

Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.

Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.

Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.

Рассмотрите фигуры с осевой и центральной симметрией.

Ось симметрии угла — биссектриса.
Ось симметрии равнобедренного треугольника — биссектриса, медиана, высота.
Оси симметрии прямоугольника проходят через середины его сторон.
У ромба две оси симметрии — прямые, содержащие его диагонали.
У квадрата 4 оси симметрии, так как он сразу квадрат, треугольник (если его сложить пополам) и ромб.
Ось симметрии окружности — любая прямая, проведенная через ее центр.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.

Видео:Видеоурок по математике "Цилиндр"Скачать

Осевая симметрия

Вот как звучит определение осевой симметрии:

Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

Читайте также: Формула диаметра штока цилиндра

В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.

Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

Пример 1. Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC относительно прямой.

Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
С другой стороны прямой отложим такие же расстояния.
Соединяем точки отрезками и строим треугольник A₁B₁C₁, симметричный треугольнику ABC.
Получаем два треугольника, симметричных относительно оси симметрии.

Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

Строим по уже известному алгоритму. Проводим прямые из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
Измеряем расстояние от вершин до точек на прямой.
Откладываем такие же расстояния на другой стороне оси симметрии.
Соединяем точки и строим треугольник A₁B₁C₁.

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно прямой l.

Измеряем расстояние от точки B до прямой l и от точки A до прямой l.
Проводим прямую от точки А через прямую l под прямым углом к прямой l, выводя за ось симметрии.
Проводим прямую от точки B через прямую l под прямым углом к прямой l, выводя за ось симметрии.
Соединяем точки A₁ и B₁ и получаем отрезок A₁B₁, симметричный данному.

Видео:ОСЬ СИММЕТРИИ ФИГУРЫ. ПРЯМОУГОЛЬНИК. Видеоурок | МАТЕМАТИКА 5 классСкачать

Центральная симметрия

Теперь поговорим о центральной симметрии — вот ее определение:

Центральной симметрией называется симметрия относительно точки.

Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах на 8 марта.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.

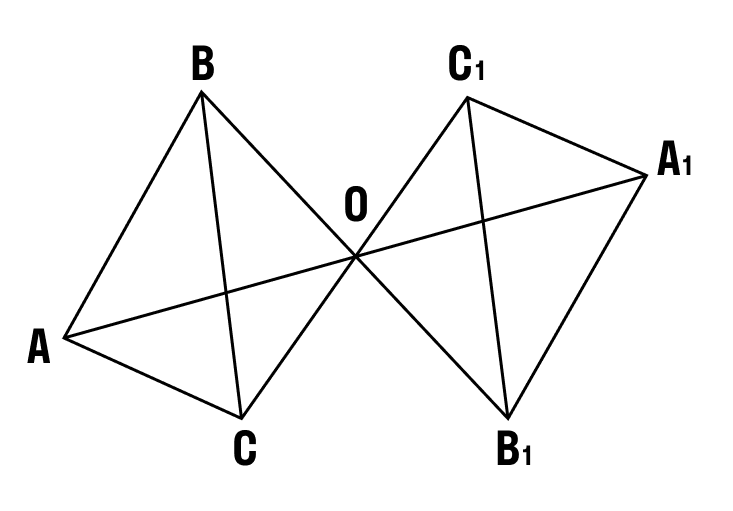
Пример 1: Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC, относительно центра (точки О).

Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
Получившиеся точки соединяем отрезками A₁B₁ A₁C₁ B₁C₁.
Получаем треугольник A₁B₁C₁, симметричный треугольнику ABC, относительно центра.

Пример 2. Постройте треугольник A₁B₁C₁, симметричный треугольнику ABC, относительно центра (точки О).

По аналогии с предыдущим примером сначала соединяем точки ABC с точкой O.
Выводим прямые за точку О.
Измеряем отрезки AO, BO, CO и отмеряем такие же на противоположной стороне.
Получаем два центрально-симметричных треугольника.

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно центра (точки О).

Измеряем расстояние от точки B до точки О и от точки А до точки О.
Проводим прямую из точки А через точку О и выводим ее на другую сторону.
Проводим прямую из точки B через точку О и выводим ее на другую сторону.
Чертим на противоположной стороне отрезки равные отрезкам АО и OB.
Соединяем точки A₁ и B₁ и получаем отрезок A₁B₁, симметричный данному.

Видео:Прямоугольник. Ось симметрии. 5-6 классСкачать

Задачи на самопроверку

В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!

Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.

Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:

Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная

Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М₁ и N₁ — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М₁N₁.