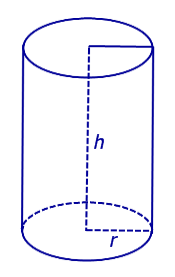
Истинная величина сечения цилиндра (3 видео)

Цилиндром будет называться геометрическое тело, полученное при ограничении цилиндрической поверхности двумя параллельными плоскостями — основаниями цилиндра. Если в основании цилиндра лежит окружность, а образующая перпендикулярна основанию, то цилиндр называется прямым круговым.

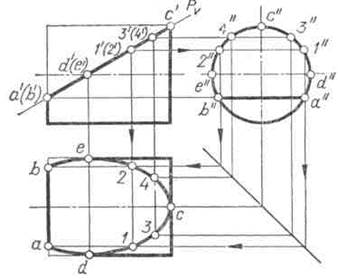
Линия сечения строится также при помощи опорных точек — точек пересечения секущей плоскости с очерковыми образующими и осью цилиндра. Но необходимо взять также промежуточные точки для более точного построения линии сечения. На рисунке 49 показано построение проекций сечения цилиндра фронтально — проецирующей плоскостью S. Так как цилиндр является проецирующей поверхностью, то горизонтальная проекция сечения совпадает с секущей плоскостью и на профильной проекции получим эллипс. Точки 2 и 3 будут являться границей видимости линии сечения для профильной плоскости.

Натуральную величину сечения можно определить способом вращения. Ось вращения выбираем в точке 1 и вращаем секущую плоскость до положения, параллельного горизонтальной плоскости. На горизонтальной плоскости получим эллипс, который будет являться натуральной величиной сечения цилиндра.

Разверткой цилиндра является прямоугольник с высотой, равной высоте цилиндра, и длиной, равной длине окружности основания 2πR. Для того, чтобы построить развертку усеченной части, основание цилиндра делят на равные части, тем самым аппроксимируя цилиндрическую поверхность призматической. Разделим окружность основания на 12 равных частей и отложим их вдоль горизонтальной линии развертки, по вертикали отложим высоту цилиндра (рис. 50).

Затем на полученных образующих отметим высоты точек сечения. Пристроим окружность основания и натуральную величину сечения.

Конус — это геометрическое тело, полученное путем ограничения конической поверхности плоскостью. Если в основании конуса лежит окружность, а высота попадает в центр основания, то конус называется прямым круговым.

На рисунке 51 построено сечение конуса фронтально — проецирующей плоскостью. Точки сечения находим при помощи вспомогательных секущих плоскостей. Точки С и D являются границей видимости для профильной проекции сечения.

Натуральную величину сечения находим способом вращения. Ось вращения выбираем в точке D и поворачиваем секущую плоскость до положения, параллельного горизонтальной плоскости проекций. Из горизонтальных проекций точек проводим линии, перпендикулярные оси вращения. Натуральной величиной сечения будет являться эллипс.

Развертка конуса является круговым сектором с радиусом, равным длине образующей конуса и длиной дуги, равной длине окружности основания конуса. Делим основание конуса на 12 равных частей и откладываем их по дуге на развертке. Затем на соответствующих образующих нужно отложить натуральные величины высот точек сечения. Чтобы получить полную развертку усеченной части, пристраиваем основание и натуральную величину сечения. На рисунке 52 показано построение развертки конуса.

1. Как образуется цилиндрическая поверхность?

2. Если секущая цилиндр плоскость фронтально проецирующая, то где будут лежать горизонтальные проекции точек сечения?

3. Какими способами можно определять натуральную величину фигуры сечения?

4. Какой геометрической фигурой является развертка боковой поверхности цилиндра? Конуса?

5. Для чего нужно разбивать окружность основания на некоторое количество равных частей?

6. Как построить развертку конической поверхности?

7. Как получить из полной развертки поверхности развертку ее усеченной части?

Содержание

Истинная величина сечения цилиндра
Цилиндры
Основные определения и свойства цилиндра
Сечения цилиндра
Объем цилиндра. Площадь боковой поверхности цилиндра. Площадь полной поверхности цилиндра
Истинная величина сечения цилиндра
Сечение плоскостью призмы, пирамиды, цилиндра и конуса
🔥 Видео

Видео:Построение усеченного цилиндра с сечением в натуральную величинуСкачать

Истинная величина сечения цилиндра

Контрольные задания по теме:
Рабочая тетрадь задача 68, задача 69

Читайте также: Температура воздух в цилиндре 7 градусов

1. Как образуется цилиндрическая поверхность?

3. Какими способами можно определять натуральную величину фигуры сечения?

4. Какой геометрической фигурой является развертка боковой поверхности цилиндра? Конуса?

5. Для чего нужно разбивать окружность основания на некоторое количество равных частей?

6. Как построить развертку конической поверхности?

7. Как получить из полной развертки поверхности развертку ее усеченной части?

Видео:Усеченный цилиндр: проекции сечения, изометрия, развертка поверхностиСкачать

Цилиндры

Видео:Построить сечение цилиндра с плоскостью общего положения.Скачать

Основные определения и свойства цилиндра

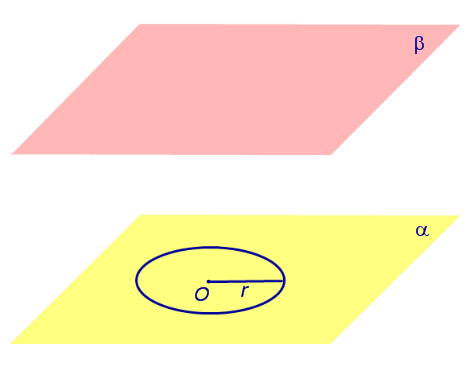
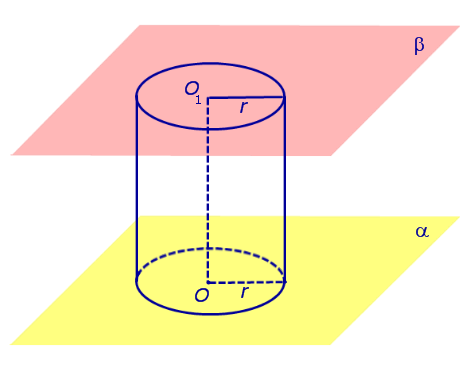
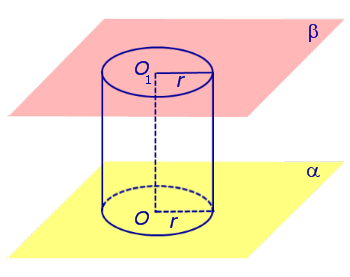
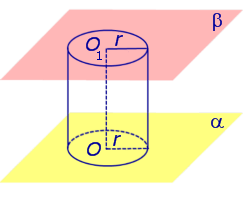
Если из каждой точки окружности опустить перпендикуляр на плоскость β , то основания этих перпендикуляров образуют на плоскости β окружность радиуса r , центр O₁ которой является основанием перпендикуляра, опущенного из точки O на плоскость β (рис.2).

Отрезок перпендикуляра, опущенного из любой точки окружности с центром O на плоскость β , который заключен между плоскостями α и β , называют образующей цилиндра .

Совокупность всех образующих цилиндра называют цилиндрической поверхностью .

Фигуру, ограниченную цилиндрической поверхностью и плоскостями α и β, называют цилиндром .

Отрезок OO₁ называют осью цилиндра .

Радиус окружности Радиус окружности на плоскости α с центром в точке O называют радиусом цилиндра .

Круги с центрами O и O₁ на плоскостях α и β , называют основаниями цилиндра .

Замечание 1. Цилиндрическую поверхность часто называют боковой поверхностью цилиндра . Боковая поверхность цилиндра и основания цилиндра вместе составляют полную поверхность цилиндра .

Читайте также: Крышка блока цилиндров ваз 2107

Замечание 2. Каждая образующая цилиндра параллельна оси цилиндра, а длина каждой образующей цилиндра равна высоте цилиндра.

Замечание 3. Прямая OO₁ является осью симметрии цилиндра, а середина отрезка OO₁ является центром симметрии цилиндра.

Видео:Задание 38. Как построить УСЕЧЕННЫЙ ЦИЛИНДР. Построение НВ фигуры сечения. Часть 1Скачать

Сечения цилиндра

Определение 2. Сечением цилиндра называют пересечение цилиндра с плоскостью.
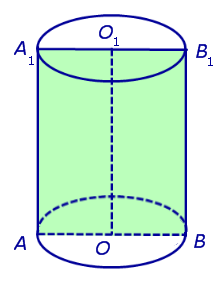
Если сечение проходит через ось цилиндра, то такое сечение называют осевым сечением цилиндра (рис. 3).

На рисунке 3 изображено одно из осевых сечений цилиндра – прямоугольник AA₁B₁B .

Замечание 4. Каждое осевое сечение цилиндра с радиусом r и высотой h является прямоугольником со сторонами 2r и h .

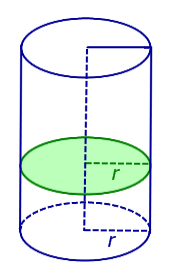
Определение 3. Перпендикулярным сечением цилиндра называют сечение, перпендикулярное оси цилиндра (рис. 4).

Замечание 5. Любым перпендикулярным сечением цилиндра будет круг радиуса r .

Замечание 6. Более подробно случаи взаимного расположения цилиндра и плоскости рассматриваются в разделе нашего справочника «Взаимное расположение цилиндра и плоскости в пространстве».

Видео:2_Натуральная величина сеченияСкачать

Объем цилиндра. Площадь боковой поверхности цилиндра.
Площадь полной поверхности цилиндра

Для цилиндра с радиусом r и высотой h (рис. 5)

введем следующие обозначения

V	объем цилиндра
S_бок	площадь боковой поверхности цилиндра
S_полн	площадь полной поверхности цилиндра
S_осн	площадь основания цилиндра

Тогда справедливы следующие формулы для вычисления объема, площади боковой и полной поверхности цилиндра:

при помощи предельного перехода, когда число сторон правильной призмы n неограниченно возрастает. Однако доказательство этого факта выходит за рамки школьной программы.

Видео:сечение цилиндраСкачать

Истинная величина сечения цилиндра

· рассмотреть основные виды сечений цилиндра

Время реализации занятия: 45 минут

II Проверка домашнего задания

III Изучение нового материала

Сечение цилиндра плоскостью, параллельной его оси, представляет собой прямоугольник (рис. 1, а). Две его стороны — образующие цилиндра, а две другие — параллельные хорды оснований. В частности, прямоугольником является осевое сечение. Это — сечение цилиндра плоскостью, проходящей через его ось (рис. 1, б).

Плоскость, параллельная плоскости основания цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.

Пусть β — плоскость, параллельная плоскости основания цилиндра (рис. 2). Параллельный перенос в направлении оси цилиндра, совмещающий плоскость Р с плоскостью основания цилиндра, совмещает сечение боковой поверхности плоскостью Р с окружностью основания. Теорема доказана.

IV Закрепление изученного материала

Осевое сечение цилиндра — квадрат, площадь которого Q. Найдите площадь основания цилиндра.

Сторона квадрата равна IQ . Она равна диаметру основания. Поэтому площадь основания равна:

Видео:усеченный цилиндр-ортогональные проекции-изометрия-разверткаСкачать

Сечение плоскостью призмы, пирамиды, цилиндра и конуса

СЕЧЕНИЕ ГЕОМЕТРИЧЕСКИХ ТЕЛ ПЛОСКОСТЬЮ

В заданиях на построение усеченных геометрических тел можно выделить следующие задачи: 1) построение усеченного тела в системе трех плоскостей проекций; 2) определение истинной величины фигуры сечения; 3) построение развертки усеченного тела и 4) вычерчивание его аксонометрической проекции. Ниже помещены рекомендации по решению каждой из перечисленных задач.

Вначале по положению секущей плоскости определяют вид фигуры сечения и в зависимости от формы геометрического тела выбирают прием построения проекций сечения. В заданиях секущие плоскости занимают проецирующее положение, поэтому одна проекция сечения задается. Недостающие проекции фигуры сечения призмы или пирамиды строят по точкам пересечения их ребер с заданной плоскостью. Если же плоскость пересекает поверхность вращения по лекальной кривой, то начинают с определения ее характерных точек.

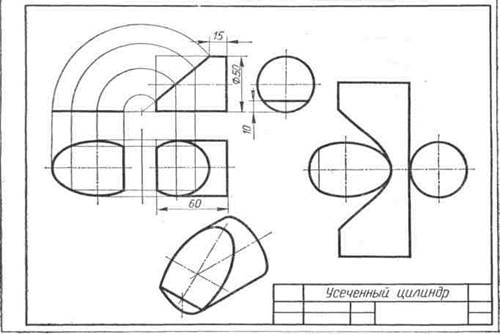
Например, фронтально проецирующая плоскость Р (рис. 106) пересекает цилиндр по неполному эллипсу. Его характерными точками являются: 1) А и В — точки, принадлежащие линии пересечения плоскости Р с основанием цилиндра; 2) С — конец большой оси эллипса; 3) D и Е — концы малой оси эллипса и они же точки, лежащие на очерковых образующих цилиндра Последовательность нахождения точек эллипса указана стрелками на примере промежуточных точек 1 и 2.

Истинную величину фигуры сечения определяют с помощью способа перемены плоскостей проекций или вращения. Если применяют способ перемены плоскостей проекций, то дополнительную плоскость задают параллельно секущей плоскости. Дополнительную плоскость совмещают с основной плоскостью проекций так, чтобы новая проекция сечения не наложилась на имеющиеся проекции. При использовании способа вращения ось вращения целесообразно располагать в секущей плоскости и на некотором расстоянии от тела.

Читайте также: Повышение цилиндров патологических в моче

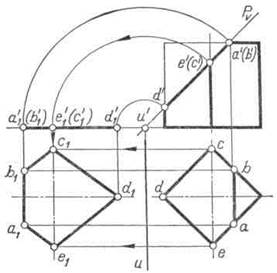
Для примера показано положение оси вращения U (рис. 107) при определении истинной величины сечения четырехугольной призмы фронтально проецирующей плоскостью Р.

Построение развертки усеченного тела начинают с вычерчивания развертки его полной боковой поверхности. Далее на нее наносят линии сечения и пристраивают к ней остальные части развертки — основания и фигуру сечения. Если какие-либо элементы, необходимые для построения развертки, на проекциях искажены, то предварительно определяют их истинную величину.

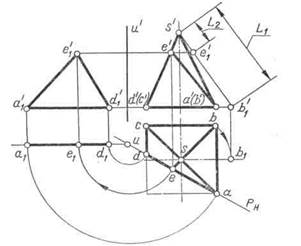
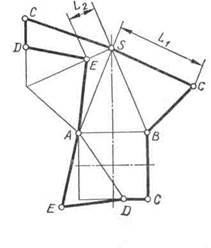
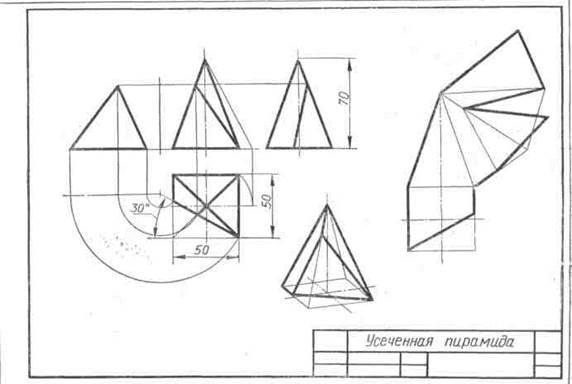
Например, для построения развертки правильной усеченной четырехугольной пирамиды (рис. 108) необходимо определить истинную величину фигуры сечения — треугольника ADE и длину одного из ее боковых ребер, например ребра SB. Для определения истинной величины этих элементов их поворачивают до положения, параллельного плоскости V. Треугольник ADE повернут вокруг оси U, а ребро SB — вокруг высоты пирамиды. Далее строят развертку согласно рекомендациям в следующем порядке: задают положение вершины S; вычерчивают развертку полной боковой поверхности пирамиды; наносят на нее линии сечения DE и AE с помощью отрезков SE = = s ′ e′₁ = L₂ и DC = dc; пристраивают к ребру основания АВ фигуру усеченного основания— четырехугольник ABCD = abcd и к его стороне AD — треугольник ADE = a′₁e′₁ d′₁.

Усеченные тела на аксонометрической проекции вначале вычерчивают целыми. Далее изображают проекцию сечения и контурными линиями обводят усеченную часть тела.

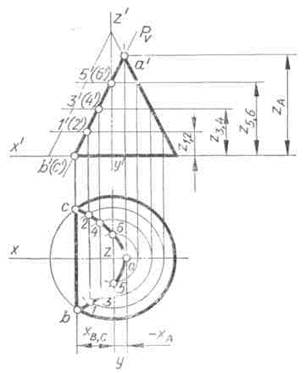
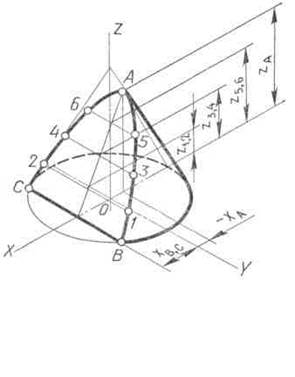
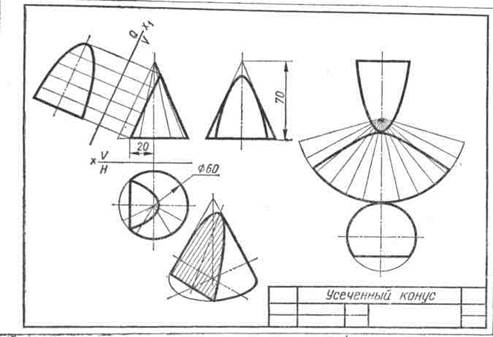
Для примера на рис. 109 вычерчена изометрическая проекция конуса, усеченного фронтально проецирующей плоскостью Р по параболе. Параболу на изометрической проекции начинают строить с ее вершины А. Эту точку получают с помощью координаты—х_А. Проекции нижних точек параболы В и С строят по координате х_В, _С. Соединив точку А с серединой отрезка ВС, получают проекцию оси симметрии параболы. Для построения ее промежуточных точек откладывают по оси конуса от его основания отрезки, равные координатам z_1,2, z_3,1, z_5,6. Через концы отложенных отрезков проводят прямые, параллельные оси координат X, до пересечения с осью симметрии параболы. Через полученные точки проводят хорды параболы, которые параллельны ее нижней хорде ВС. Длину каждой хорды замеряют на горизонтальной проекции усеченного конуса и откладывают на соответствующей хорде изометрической проекции.

Задание 23. Усеченные геометрические тела. Построить заданные усеченные геометрические тела (призму, пирамиду, цилиндр, конус) в системе трех плоскостей проекций, определить истинные величины фигур сечения, вычертить развертки усеченных тел и их аксонометрические проекции. Вид аксонометрической проекции указан в табл. 13.

Варианты задания	Прямоугольная изометрическая проекция	Прямоугольная диметрическая проекция
номера задач
I, III, V, VII, IX, XI, XIII, XV	1, 3	2, 4
II, IV, VI, VIII, X, XII,XIV	2, 4	1, 3
XVI	1, 4	2, 3

Изображение каждого геометрического тела располагают на листе формата A3.

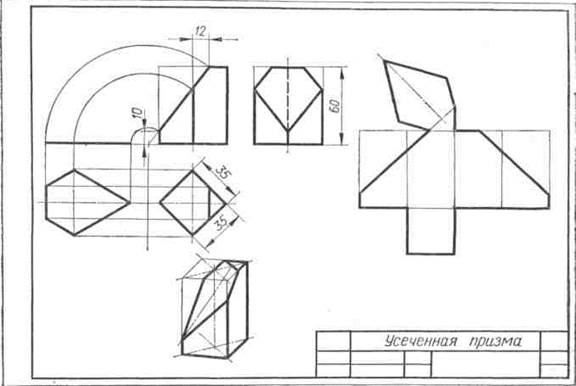
Образцы выполненного задания с разными вариантами оформления приведены на рис. 110—113.

Работу над заданием следует начинать с компоновки чертежа, которая довольно трудоемка из-за большого количества изображений. Габариты горизонтальной, фронтальной, профильной и аксонометрической проекций тела подсчитывают по заданным проекциям. Размеры сечения и развертки определяют приблизительно или делают на черновике нужные построения.

Сократить работу с предлагаемым заданием можно, уменьшив число геометрических тел или упростив содержание задания. Например, отказаться от вычерчивания аксонометрической проекции тела или не строить его развертку.