Из чего сделан цилиндр по физике (4 видео)

Цилиндром ( прямым круговым цилиндром ) называется тело, состоящее из двух кругов ( оснований цилиндра ), совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие при параллельном переносе точки этих кругов. Отрезки, соединяющие соответствующие точки окружностей оснований, называются образующими цилиндра.

Цилиндр — тело, которое ограничено цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями, пересекающими образующие данной поверхности.

Цилиндрическая поверхность — поверхность, которая образуется движением прямой линии вдоль некоторой кривой. Прямую называют образующей цилиндрической поверхности, а кривую линию — направляющей цилиндрической поверхности.

Боковая поверхность цилиндра — часть цилиндрической поверхности, которая ограничена параллельными плоскостями.

Основания цилиндра — части параллельных плоскостей, отсекаемые боковой поверхностью цилиндра.

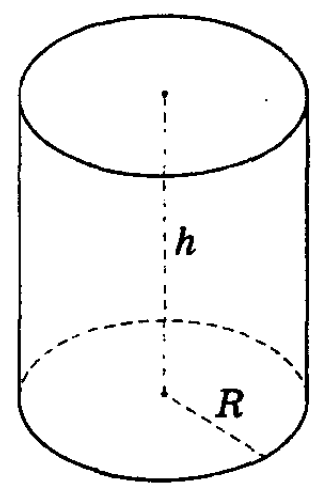
Цилиндр называется прямым (См.Рис.1), если его образующие перпендикулярны плоскостям оснований. В противном случае цилиндр называется наклонным.

Круговой цилиндр — цилиндр, основания которого являются кругами.

Прямой круговой цилиндр ( просто цилиндр ) – это тело, полученное при вращении прямоугольника вокруг одной из его сторон. См.Рис.1.

Радиус цилиндра – радиус его основания.

Образующая цилиндра — образующая цилиндрической поверхности.

Высотой цилиндра называется расстояние между плоскостями оснований. Осью цилиндра называется прямая, проходящая через центры оснований. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.

Ось цилиндра параллельна его образующей и является осью симметрии цилиндра.

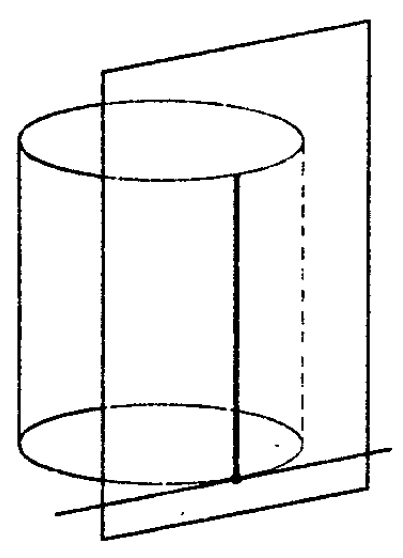
Плоскость, проходящая через образующую прямого цилиндра и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью цилиндра. См.Рис.2.

Развёртка боковой поверхности цилиндра — прямоугольник со сторонами, равными высоте цилиндра и длине окружности основания.

Площадь боковой поверхности цилиндра — площадь развёртки боковой поверхности. $$S_ =2\pi\cdot rh$$ , где h – высота цилиндра, а r – радиус основания.

Площадь полной поверхности цилиндра — площадь, которая равна сумме площадей двух оснований цилиндра и его боковой поверхности, т.е. выражается формулой: $$S_ =2\pi\cdot r^2 + 2\pi\cdot rh = 2\pi\cdot r(r+h)$$ , где h – высота цилиндра, а r – радиус основания.

Объем всякого цилиндра равен произведению площади основания на высоту: $$V = S\cdot h$$ Объем круглого цилиндра: $$V=\pi r^2 \cdot h$$ , где (r — радиус основания).

Призма есть частный вид цилиндра (образующие параллельны боковым ребрам; направляющая — многоугольник, лежащий в основании). С другой стороны, произвольный цилиндр можно рассматривать как выродившуюся («сглаженную») призму с очень большим числом очень узких граней. Практически цилиндр неотличим от такой призмы. Все свойства призмы сохраняются и в цилиндре.

Содержание

Из чего сделан цилиндр по физике
Что такое цилиндр: определение, элементы, виды, варианты сечения
Определение цилиндра
Основные элементы цилиндра
Геометрические тела. Цилиндр.
Формулы нахождения элементов цилиндра.
ГДЗ учебник по физике 7 класс Перышкин. №1 Определение цены деления измеррительного прибора. Номер №1
Решение
📸 Видео

Видео:ЦилиндрСкачать

Из чего сделан цилиндр по физике

Гриша нашёл в кабинете физики отполированный цилиндрик и заинтересовался, из какого материала он сделан — из олова или из железа. Гриша прочитал в справочнике, что плотности железа и олова отличаются не более чем на 10%, а вот их удельные теплоёмкости различаются почти в два раза: 250 Дж/(кг · °С) для олова и 460 Дж/(кг · °С) для железа. Для определения материала цилиндра было решено провести термодинамический опыт. Гриша налил в пластиковый калориметр m_в = 100 г холодной воды при комнатной температуре t_х = 23 °С. В горячую воду, которая имела температуру t_г = 50,5 °С градуса, Гриша поместил цилиндрик. После того, как цилиндрик нагрелся, Гриша перенёс его в калориметр и затем измерил установившуюся температуру в калориметре — она оказалась равной t_у = 25,5 °С. После этого Гриша взвесил цилиндрик, его масса оказалась равной m_ц = 168 г. Теплоёмкостью калориметра Гриша решил пренебречь. Удельная теплоёмкость воды c_в = 4200 Дж/(кг · °С) ему была известна.

Читайте также: Момент инерции диска стержня цилиндра

1) Какое количество теплоты получила вода от цилиндрика?

2) Рассчитайте удельную теплоёмкость материала цилиндрика и определите, из какого металла он изготовлен.

3) Когда Гриша почти закончил обработку результатов своего эксперимента, учитель сказал ему, чтобы он не забыл учесть теплоёмкость калориметра. Масса калориметра составляла m_к = 40 г, а удельная теплоёмкость пластмассы по данным справочника была равна c_к = 210 Дж/(кг · °С). Может ли Гриша, с учётом этих сведений, утверждать, что он не ошибся в определении материала, из которого сделан цилиндрик?

1) Количество теплоты, полученное водой:

2) Составим уравнение теплового баланса воды и цилиндрика:

Видно, что полученная удельная теплоёмкость совпадает с удельной теплоёмкостью олова. То есть цилиндрик оловянный.

3) Будем считать, что калориметр нагрелся до температуры воды t_у = 25,5 °С. В этом случае уравнение теплового баланса можно записать так:

Тогда для значения удельной теплоёмкости цилиндрика можно получить:

Видно, что полученное значение практически не отличается от найденного ранее. Значит, материал цилиндрика определён правильно.

I) записаны положения теории, физические законы, закономерности, формулы и т. п., применение которых необходимо для решения задачи выбранным способом;

II) проведены нужные рассуждения, верно осуществлена работа с графиками, схемами, таблицами (при необходимости), сделаны необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями; часть промежуточных вычислений может быть проведена «в уме»; задача может решаться как в общем виде, так и путём проведения вычислений непосредственно с заданными в условии численными значениями);

Видео:Как белое сделать черным. Natürlich!Скачать

Что такое цилиндр: определение, элементы, виды, варианты сечения

В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения одной из самых распространенных трехмерных геометрических фигур – цилиндра. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Видео:Вращающиеся цилиндрыСкачать

Определение цилиндра

Далее мы подробно остановимся на прямом круговом цилиндре как самой популярной разновидности фигуры. Другие ее виды будут перечислены в последнем разделе данной публикации.

Прямой круговой цилиндр – это геометрическая фигура в пространстве, полученная путем вращения прямоугольника вокруг своей стороны или оси симметрии. Поэтому такой цилиндр иногда называют цилиндром вращения.

Цилиндр на рисунке выше получен в результате вращения прямоугольного треугольника ABCD вокруг оси O₁O₂ на 180° или прямоугольников ABO₂O₁/O₁O₂CD вокруг стороны O₁O₂ на 360°.

Видео:Как работает двигатель внутреннего сгорания автомобиля?Скачать

Основные элементы цилиндра

Основания цилиндра – два одинаковых по размеру/площади круга с центрами в точках O₁ и O₂.
R – радиус оснований цилиндра, отрезки AD и BC – диаметры (d).
O₁O₂ – ось симметрии цилиндра, одновременно является его высотой (h).
l (AB, CD) – образующие цилиндра и одновременно с этим стороны прямоугольника ABCD. Равны высоте фигуры.

Развёртка цилиндра – боковая (цилиндрическая) поверхность фигуры, развернутая в плоскость; является прямоугольником.

длина данного прямоугольника равна длине окружности основания цилиндра ( 2πR );
ширина равна высоте/образующей цилиндра.

Примечание: формулы для нахождения площади поверхности и объема цилиндра представлены в отдельных публикациях.

Видео:Как возникает подъёмная сила крыла?Скачать

Геометрические тела. Цилиндр.

Цилиндр − это геометрическое тело, которое ограничено цилиндрической поверхностью и 2-мя плоскостями, которые параллельны и пересекают ее.

ABCDEFG и abcdefg — это основания цилиндра. Расстояние между основаниями (KM) – высота цилиндра.

Цилиндрические сечения боковой поверхности кругового цилиндра.

Сечения, которые идут параллельно к основанию, будут являться кругами одного радиуса. Сечения, которые параллельны образующим цилиндра — это пары параллельных прямых (AB || CD). Сечения, не параллельные ни основанию, ни образующим, являются эллипсами.

Цилиндрическая поверхность образуется посредством движения прямой параллельно самой себе. Точка прямой, которая выделена, перемещается вдоль заданной плоской кривой – направляющей. Эта прямая называется образующей цилиндрической поверхности.

Прямой цилиндр – это такой цилиндр, в котором образующие перпендикулярны основанию. Если образующие цилиндра не перпендикулярны основанию, то это будет наклонный цилиндр.

Круговой цилиндр – цилиндр, основанием которого является круг.

Круглый цилиндр – такой цилиндр, который одновременно и прямой, и круговой.

Прямой круговой цилиндр определяется радиусом основания R и образующей L, которая равна высоте цилиндра H.

Призма – это частный случай цилиндра.

Видео:Гидравлическая машинаСкачать

Формулы нахождения элементов цилиндра.

Площадь боковой поверхности прямого кругового цилиндра:

Площадь полной поверхности прямого кругового цилиндра:

Объем прямого кругового цилиндра:

Прямой круговой цилиндр со скошенным основанием либо кратко скошенный цилиндр определяют с помощью радиуса основания R, минимальной высоты h₁ и максимальной высоты h₂.

Площадь боковой поверхности скошенного цилиндра:

Площадь оснований скошенного цилиндра:

Площадь полной поверхности скошенного цилиндра:

Объем скошенного цилиндра:

S_бок — площадь боковой поверхности;

Видео:Пневмоцилиндр. Конструкция и принцип работы пневматического цилиндраСкачать

ГДЗ учебник по физике 7 класс Перышкин. №1 Определение цены деления измеррительного прибора. Номер №1

Цель работы:
Определить цену деления измерительного цилиндра (мензурки), научиться пользоваться им и определять с его помощью объём жидкости.
Приборы и материалы:
Измерительный цилиндр (мензурка), стакан с водой, небольшая колба и другие сосуды.
Указания к работе:
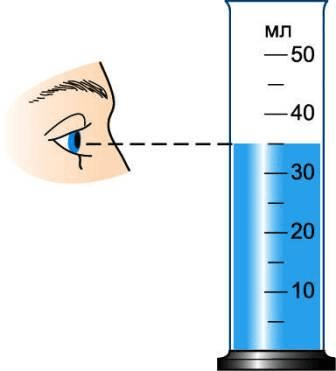
1 . Рассмотрите измерительный цилиндр (рис. 198 ), обратите внимание на его деления. Ответьте на следующие вопросы.
1 )Какой объём жидкости вмещает измерительный цилиндр, если жидкость налита:
а) до верхнего штриха;
б) до первого снизу штриха, обозначенного цифрой, отличной от нуля?
2 )Какой объём жидкости помещается:
а) между 2 −м и 3 −м штрихами, обозначенными цифрами;
б) между соседними (самыми близкими) штрихами мензурки?
2 . Как называется последняя вычисленная вами величина? Как определяют цену деления шкалы измерительного прибора?
Запомните: прежде чем проводить измерения физической величины с помощью измерительного прибора, определите цену деления его шкалы.
3 . Рассмотрите рисунок 7 учебника и определите цену деления изображённой на нём мензурки.
4 . Налейте в измерительный цилиндр воды, определите и запишите, чему равен объём налитой воды.
Примечание. Обратите внимание на правильное положение глаза при отсчёте объёма жидкости. Вода у стенок сосуда немного приподнимается, в средней же части сосуда поверхность жидкости почти плоская. Глаз следует направить на деление, совпадающее с плоской частью поверхности (рис. 198 ).
5 . Налейте полный стакан воды, потом осторожно перелейте воду в измерительный цилиндр. Определите и запишите с учётом погрешности, чему равен объём налитой воды. Вместимость стакана будет такой же.
6 . Таким же образом определите вместимость колбы, аптечных склянок и других сосудов, которые находятся на вашем столе.
7 . Результаты измерений запишите в таблицу 6 .

рис. 198 .

рис. 7 . Измерительный цилиндр.
Таблица 6 .

Решение

Прежде чем проводить измерения физической величины с помощью измерительного прибора нужно определите цену деления его шкалы.
Для определения цены деления необходимо взять 2 соседних числа, найти их разницу (от большего отнять меньшее), а затем разделить полученное число на количество маленьких штрихов между этими числами.
На шкале цилиндра возьмём, к примеру, числа 20 и 30 .
Таким образом, цена каждого деления будет равна
$\frac = \frac $ = 5 мл.
1 .

1, а) Если жидкость налита до верхнего штриха, измерительный цилиндр вмещает 50 мл жидкости.
1, б) Если жидкость налита до первого снизу штриха, обозначенного цифрой, отличной от нуля, измерительный цилиндр вмещает 10 мл жидкости.
2, а) Между 2 − м и 3 −м штрихами, обозначенными цифрами, помещается 10 мл жидкости (например, возьмём штрихи 20 мл и 30 мл).
2, б) Между соседними (самыми близкими) штрихами мензурки (например, возьмём штрихи 30 и 35 ), помещается 5 мл жидкости.
2 . Последняя вычисленная нами величина является ценой деления измерительного цилиндра.
3 . На шкале цилиндра возьмём, к примеру, числа 50 и 60 . Количество маленьких штрихов между этими числами − 2 .
Таким образом, цена каждого деления будет равна
$\frac = \frac $ = 5 мл.
4 . Объём налитой воды равен 35 мл или 35 $см^ $ .
5 . Погрешность измерений равна половине цены деления шкалы измерительного прибора. Цена деления цилиндра − 5 мл, следовательно, погрешность измерения равна $\frac $ мл = 2,5 мл.
Объём налитой в полный стакан воды с учётом погрешности будет равен ( 200 ±∆ 2,5 ) мл ( $см^ $ ).
6 .
Таблица 6 .
| № опыта |Название сосуда| Объём жидкости $V_ , см^ $ |Вместимость сосуда, $V_ , см^ $ |
| −−− | −−− | −−− | −−− |
| 1 | стакан | 200 | 200 |
| 2 | колба | 50 | 50 |
| 3 | пузырёк | 30 | 30 |

Вывод. В ходе лабораторной работы мы определелили цену деления измерительного цилиндра, научились им пользоваться и научились с его помощью определять объём жидкости.