Из квадрата площадь которого равна q свернули боковую поверхность цилиндра

Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Из квадрата, площадь которого равна Q, свернули боковую поверхность цилиндра. Найдите площадь основания этого цилиндра.

Искать площадь АОВD бессмысленно — это самопересекающийся четырехугольник.

Или приложите чертеж. Я буду искать площадь четырехугольника АВОD.

Возможны 2 случая — окружность вписана в треугольник DMC, или в АFD.

Во втором случае четырехугольник невыпуклый, но всё-же его площадь можно вычислить.

Если я где ошибся с вычислениями, прошу прощения — очень спешу.

Объяснение: Мы знаем что углы треугольника в сумме составляют 180 градусов, а также сумма внешнего и внутреннего составляет 180 градусов, значит 180-(64+37)=89 градусов- это третий внутренний угол,

теперь ищем внешние углы, 180 — 37 = 143 градуса- 1 внешний угол,

180 — 64 = 116 градусов- 2 внешний угол, 180 — 89 = 91 градусов- это 3 внешний угол. Вот так

Во-первых, они оба прямоугольные. Остается доказать равенство одной из пар углов. Пусть ∠A=α⇒∠B=90°-α⇒∠FCB=90°-(90°-α)=α

Итак, ΔACF и ΔCBF прямоугольные и ∠A первого треугольника равен ∠FCB второго. Значит, эти треугольники подобны

Видео:№544. Из квадрата, диагональ которого равна d, свернута боковая поверхность цилиндра.Скачать

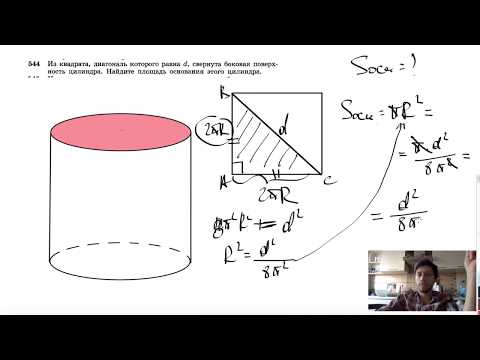
Из квадрата, площадь которого равна Q, свернули боковую поверхность цилиндра. Найдите площадь основания этого цилиндра.

Видео:60. Площадь поверхности цилиндраСкачать

Ответы

расположим сферу так, чтобы плоскость треугольника была горизонтальной. тогда вид сверху даёт нам окружность в которую вписан треугольник авс. примем ав=2, вс=4 корня из2, ас=6. обратим внимание, что ас квадрат=ав квадрат+ вс квадрат. или 36=4+32. отсюда -треугольник авс прямоугольный. угол в прямой(против большей стороны). центр описанной окружности в прямоугольном треугольнике лежит на середине гипотенузы.обозначим эту точку о1. ао1=со1=3. это значит, чтоо1 -центр круга полученного сечением сферы плоскостью в которой лежит треугольник авс. тогда расстояние от центра сферы до плоскости треугольника авс будет равно о1о. где о центр сферы. рассмотрим вид сбоку. в проекции получаем окружность радиусом равным радиусу сферы r. проекция плоскости треугольника авс-хорда ас. проведём радиусы оа и ос. проведём перпендикуляр оо1=4(по условию). к ас. тогда по теореме пифагора r=корень из(о1с квадрат+ оо1квадрат)=корень из (9+16)=5.

i ab i² = (2 — (-6))² + (4 — 1)² = 64 + 9 = 73

i ac i² = (2 — (-6))² + (-2 — 1)² = 64 + 9 = 73

i bc i² = (2 — 2)² + (-2 — 4)² = 0 + 36 = 36

i ab i = i ac i , поэтому треугольник авс — равнобедренный и высота, проведенная из вершины а, является также медианой.

Читайте также: Как еще называют цилиндр

если м — середина стороны вс, то м = ((2 + 2)/2; (4 + (-2))/2) = (2; 1) и. следовательно i am i = √ ((2 — (-6))² + (1 — 1)²) = √ 64 = 8.

Видео:№558. Разверткой боковой поверхности конуса является сектор с дугой α. Найдите α, еслиСкачать

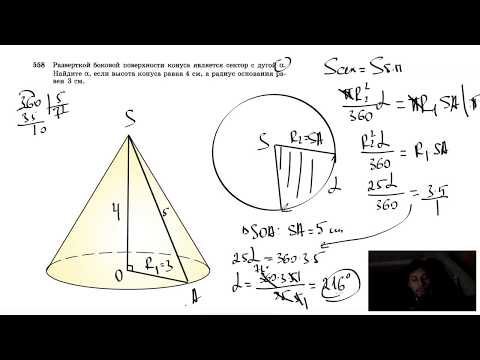
Из квадрата, площадь которого равна Q, свернули боковую поверхность цилиндра. Найдите площадь основания этого цилиндра. С рисунком

Видео:Нахождение площади боковой поверхности цилиндраСкачать

Ответы

если в первом треугольнике угол при вершине равен 24 градуса,то угол при основании будет равен (180-24): 2=78градусов.то есть у нас получается треугольник с углами при основании по 78градусов и углом при вершине 24 градуса

во втором трегуольнике угол при основании равен 78 градусов,а если треугольник равнобедренный,то и 2ой угол при основании также равен 78 градусов.угол при вершини этого треугольника будет равен 180-78-78=24.то есть получается треугольник с углами соответственно равными углам первого треугольника.следственно треугольники подобны.

расстояния от концов отрезка к плоскоси- перпендикуляры, пусть точка пересечения перпендикуляра , проведенного с точки а и плоскости — с, тогда ас=2,4м(за условиями ), а точка пересечения перпендикуляра, проведенного с точки в и плоскости — к, тогда вк=7,6м(за условиями ), расстояние от точки м до плоскости- тоже перпендикуляр, назовем его мр, где р-точка пересечения перпендикуляра, проведенного с точки м и плоскости. тогда у нас получиться фигура авкс, что будет прямоугольной трапецией, поскольку ее основания паралельны(как два перпендикуляра)в этой трапеции отрезок мр- средняя линия, поскольку соединяет середины боковых сторон трапеции. поскольку средняя линия трапеции равна полсумме ее оснований, то мр=(ас+вк): 2=(2,4+7,6): 2=10м: 2=5м ответ: 5м

cb=2c1c из этого следует вывод что угол b=30

Видео:№538. Площадь боковой поверхности цилиндра равна 5. Найдите площадь осевогоСкачать

Из квадрата, площадь которого равна Q, свернули боковую поверхность цилиндра. Найдите площадь основания этого цилиндра. С рисунком

Видео:62. Площадь поверхности конусаСкачать

Ответы

боковые стороны по хсм,х+х+се=26

дв -бисектриса и медиана, потому что треуг. равнобедреный. ев= (26-2х)/2=13-х

проведем образующие через концы отрезка ав. плоскость, проходящая через эти образующие, параллельна оси. поэтому минимальное расстояние между осью и ав равно расстоянию до этой плоскости.

«вид сверху» делает это построение понятным совсем — отрезок проектируется на основание, и искомое расстояние равно расстоянию от центра до линии проекции.

таким образом, нам надо найти длину хорды-проекции отрезка ав на основание. образующая, эта проекция и сам отрезок образуют прямоугольний треугольник с катетом 6 и гипотенузой 10. следовательно второй катет равен 8, и нам надо найти расстояние от центра окружности радиусом 5 до хорды длиной 8. (опять любимое заклинание : )) это расстояние находитс из прямоугольного треугольника, в котором гипотенуза — радиус 5, а один из катетов это половина хорды, то есть 4, поэтому

если m n k середины сторон то отрезки mn mk nm половины

сторон треугольника, который равностороний, следовательно равностороний и треугольник mnk

Видео:ОТКУДА? Как найти площадь боковой поверхности конуса? Развёртка конуса | Математика с ДетекторомСкачать

Из квадрата, площадь которого равна Q, свернули боковую поверхность цилиндра. Найдите площадь основания этого цилиндра. С рисунком

Видео:№457. Найдите сторону квадрата, площадь которого равна площади прямоугольника соСкачать

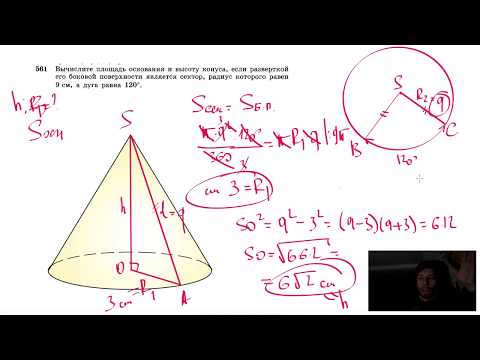
Ответы

боковые стороны по хсм,х+х+се=26

дв -бисектриса и медиана, потому что треуг. равнобедреный. ев= (26-2х)/2=13-х

проведем образующие через концы отрезка ав. плоскость, проходящая через эти образующие, параллельна оси. поэтому минимальное расстояние между осью и ав равно расстоянию до этой плоскости.

«вид сверху» делает это построение понятным совсем — отрезок проектируется на основание, и искомое расстояние равно расстоянию от центра до линии проекции.

таким образом, нам надо найти длину хорды-проекции отрезка ав на основание. образующая, эта проекция и сам отрезок образуют прямоугольний треугольник с катетом 6 и гипотенузой 10. следовательно второй катет равен 8, и нам надо найти расстояние от центра окружности радиусом 5 до хорды длиной 8. (опять любимое заклинание : )) это расстояние находитс из прямоугольного треугольника, в котором гипотенуза — радиус 5, а один из катетов это половина хорды, то есть 4, поэтому

Читайте также: Поменял задние тормозные цилиндры а их нет

если m n k середины сторон то отрезки mn mk nm половины

сторон треугольника, который равностороний, следовательно равностороний и треугольник mnk

Видео:№570. Площадь боковой поверхности конуса равна 80 см2. Через середину высоты конуса проведена плоскоСкачать

Из квадрата, площадь которого равна Q, свернули боковую поверхность цилиндра. Найдите площадь основания этого цилиндра. С рисунком

Видео:Объем и площадь поверхности цилиндра (видео 44) | Подобие. Геометрия | МатематикаСкачать

Ответы

если в первом треугольнике угол при вершине равен 24 градуса,то угол при основании будет равен (180-24): 2=78градусов.то есть у нас получается треугольник с углами при основании по 78градусов и углом при вершине 24 градуса

во втором трегуольнике угол при основании равен 78 градусов,а если треугольник равнобедренный,то и 2ой угол при основании также равен 78 градусов.угол при вершини этого треугольника будет равен 180-78-78=24.то есть получается треугольник с углами соответственно равными углам первого треугольника.следственно треугольники подобны.

расстояния от концов отрезка к плоскоси- перпендикуляры, пусть точка пересечения перпендикуляра , проведенного с точки а и плоскости — с, тогда ас=2,4м(за условиями ), а точка пересечения перпендикуляра, проведенного с точки в и плоскости — к, тогда вк=7,6м(за условиями ), расстояние от точки м до плоскости- тоже перпендикуляр, назовем его мр, где р-точка пересечения перпендикуляра, проведенного с точки м и плоскости. тогда у нас получиться фигура авкс, что будет прямоугольной трапецией, поскольку ее основания паралельны(как два перпендикуляра)в этой трапеции отрезок мр- средняя линия, поскольку соединяет середины боковых сторон трапеции. поскольку средняя линия трапеции равна полсумме ее оснований, то мр=(ас+вк): 2=(2,4+7,6): 2=10м: 2=5м ответ: 5м

cb=2c1c из этого следует вывод что угол b=30

Видео:Профильный ЕГЭ 2024 математика Ященко. Варианты 21, 22Скачать

Из квадрата, площадь которого равна q, свернули боковую поверхность цилиндра. найдите площадь основания этого цилиндра.

Видео:№561. Вычислите площадь основания и высоту конуса, если разверткой его боковой поверхностиСкачать

Ответы

для указанного тр-ка справедлива теорема пифагора: 25^2 = 24^2 + 7^2

значит он прямоугольный. наименьшая высота — это высота, опущенная на гипотенузу. она выражается через катеты и гипотенузу известной формулой:

h = (ab)/c = 24*7/25 = 168/25 = 6,72 cm

ребро будет являться высотой.

у ромба все стороны равны, значит сторона равна p/4=24/4=6 см

диагонали в ромбе делят углы,из которых они выходят, пополам.

проведем диагонали и получим 4 равных треугольника.пересекаются диагонали между собой под прямым углом.

рассмотрим один из треугольников. у него один угол будет прямым(где диаг пересек), второй 30(угол ромба делится диагональю пополам), третий соответственно 60. в треугольнике с углом 30 гр катет, лежащий напротив этого угла, равен половине гипотенузы.гипотенуза равна стороне ромба, т.е 6, значит половина диагонали будет 3 (половина стороны).вся диагональ будет 6.

вторую диагональ можно найт практически таким же обраом,рассмотрев треугольник. по т.пифагора найдем второй катет в прямоуг треуг катет в квадрате равен гипотенуза в квадр — второй катет в кв= 6*6-3*3=36-9=25

извлекая корень получим 5 — это половина диаг, вся диаг равна 10.

нам нужна меньшая, для рассчетов возьмем ее- 6 см.

в сечении будет прямоугольник.длина будет у него 6 см(диагональ), а ширина — ребро — 10 см

осевое сечение — равнобедренный прямоугольный треугольник с образующей l и основанием 2r. h=r, l=r√2. периметр 2l+2r = 2r√2+2r = 2r(1+√2) = m, отсюда r=m/2(1+√2)

💡 Видео

№698. Сумма двух противоположных сторон описанного четырехугольника равна 12 см, а радиусСкачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Пересечение двух цилиндров: объем и площадь поверхности через двойной интегралСкачать

Геометрия 11 класс (Урок№7 - Конус.)Скачать

№258. Боковое ребро правильной четырехугольной пирамиды образует угол в 60° с плоскостью основания.Скачать

№450. Найдите сторону квадрата, если его площадь равна: а) 16 см2; б) 2,25 дм2; в) 12 м2.Скачать

Нахождение длин отрезков в #стереометрическихзадачах.Скачать