Даны два цилиндра. Объём первого цилиндра равен 8. У второго цилиндра высота в 4 раза меньше, а радиус основания в 3 раза больше, чем у первого. Найдите объём второго цилиндра.
Это задание ещё не решено, приводим решение прототипа.
Объём первого цилиндра равен 12 м 3 . У второго цилиндра высота в три раза больше, а радиус основания в два раза меньше, чем у первого. Найдите объём второго цилиндра (в м 3 ).
Пусть объём первого цилиндра равен объём второго — где — радиусы оснований цилиндров, — их высоты. По условию Выразим объём второго цилиндра через объём первого:
Аналоги к заданию № 501880: 517194 517232 Все
Видео:ОБЪЕМ ЦИЛИНДРА #shorts #егэ #огэ #математика #профильныйегэСкачать
Тригонометрия
Рис.9 Оптимальная форма цилиндра при заданном объеме позволяет уменьшить расходы на материалы. Поэтому такая задача актуальна, например, при строительстве нефтехранилищ (рисунок \(9\)).
Пусть \(H\) − высота цилиндра, а \(R\) − радиус его основания. Объем и полная площадь поверхности цилиндра вычисляются по формулам \[V = \pi H,\;\;\;S = 2\pi + 2\pi RH.\] В качестве независимой переменной выберем радиус основания \(R.\) Выразим \(H\) через \(R\) (при заданном объеме \(V\) ): \[H = \frac >>.\] Исследуем площадь поверхности \(S\left( R \right)\) на экстремум. \[ + 2\pi RH > = + 2\pi R \cdot \frac >> > = + \frac > .> \] Вычисляем производную: \[ + \frac > > \right)^\prime > > = > >> > = — 2V>> >>.> \] Находим стационарные точки: \[ \;\; — 2V>> >> = 0,>\;\; > — 2V = 0>\\ \ne 0> \end ,> \right.>\;\; >>>.> \] Данное значение \(R\) соответствует минимальной площади поверхности \(S\left( R \right),\) поскольку при переходе через эту точку производная меняет знак с минуса на плюс.
Видео:Объём цилиндраСкачать
Найдем объем цилиндра. ГДЗ 10 класс алгебра Алимов Упражнения для повторения № 1527
Приветик, решим?
Из всех цилиндров, у которых периметр осевого сечения равен р, выбран цилиндр наибольшего объёма. Найти этот объём.
Решим конечно.
Вот уж не думала, что не справлюсь( Но что то никак не сходиться, спасайте! Вот условие:
Найти тангенс угла, который касательная к ( Подробнее. )
Привет. Выручайте с ответом по математике…
Найдите значение выражения ( Подробнее. )
Привет всем! Нужен ваш совет, как отвечать…
Найдите значение выражения 3,12 : 2,6-0,8.
в одном из ядерных экспериментов протон с энергией в 1МэВ движется в однородном магнитном поле по круговой траектории. какой энергией ( Подробнее. )
Замените значок * таким выражением, чтобы выполнялось равенство:
1) (*)5 = a25; 2) (*)2 = а10; 3) (*)3 = а3n; 4) (*)n = ( Подробнее. )
Читайте также: Цилиндр автомобиля это двигатель
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать
Из всех цилиндров данного объема
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной части цилиндра равен
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной части цилиндра равен
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной части цилиндра равен
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной части цилиндра равен
Найдите объем V части цилиндра, изображенной на рисунке. В ответе
Объем данной части цилиндра равен
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной части цилиндра равен
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной части цилиндра равен
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной части цилиндра равен
Если сначала найти объем целого цилиндра, то он равен 1/3 * ПИ * r^2 * H, где r=6, H=5, то есть объем цилиндра равен 60 пи, а потом разделить его на четыре, т.к. данный сектор занимает 1/4 части всего цилиндра, то получится 15. В чем дело, что не так?
Ошибка в формуле. Объём цилинлра равен произведению высоты на площадь основания.
Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной части цилиндра равен
Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной части цилиндра равен
Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной части цилиндра равен
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной фигуры равен сумме объемов цилиндра с радиусом основания 2 и высотой 3 и половины цилиндра с тем же радиусом основания и высотой 1:
Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной фигуры равен сумме объемов цилиндра с радиусом основания 2 и высотой 3 и половины цилиндра с тем же радиусом основания и высотой 1:
Добрый день,в условии указано что первая высота равна 3, а вторая 1. Почему в решении написано 0,5H(2)?
Так учитывается половина цилиндра
Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
Объем данной фигуры равен разности объемов цилиндра с радиусом основания 5 и высотой 5 и цилиндра с той же высотой и радиусом основания 2:
Видео:Объем цилиндраСкачать
Задачи на тему «Цилиндр»
\(\blacktriangleright\) Ось цилиндра – прямая, соединяющая центры его оснований.
Отрезок, соединяющий центры оснований – высота.
\(\blacktriangleright\) Образующая цилиндра – перпендикуляр, проведенный из точки границы одного основания к другому основанию.
Заметим, что образующая и высота цилиндра равны друг другу.
\(\blacktriangleright\) Площадь боковой поверхности цилиндра \( >=2\pi rh>>\) , где \(r\) – радиус основания, \(h\) – высота (или образующая).
Читайте также: Прокладка блока цилиндров двигателя 1111731191
\(\blacktriangleright\) Площадь полной поверхности цилиндра равна сумме площади боковой поверхности и площадей оснований. \[ >=2\pi rh+2\pi r^2>>\]
\(\blacktriangleright\) Объем цилиндра \( >\cdot h=\pi r^2h>>\)
Заметим, что прямой цилиндр имеет некоторое сходство с прямой призмой, только в ее основаниях лежат многоугольники (граница которых – ломаная), а в основаниях цилиндра – круги (граница которых гладкая).
Поэтому можно сказать, что боковая поверхность прямой призмы “ребристая”, а цилиндра – “гладкая”.
Про прямые круговые цилиндры \(C_1\) и \(C_2\) известно, что у \(C_1\) радиус основания в два раза больше, чем у \(C_2\) , но у \(C_2\) высота в три раза больше, чем у \(C_1\) . Найдите отношение объёма цилиндра \(C_2\) к объёму \(C_1\) .
Обозначим высоту цилиндра \(C_1\) через \(h_1\) , а высоту цилиндра \(C_2\) через \(h_2\) . Обозначим радиус основания цилиндра \(C_1\) через \(r_1\) , а радиус основания цилиндра \(C_2\) через \(r_2\) . Тогда \[r_1 = 2r_2,\qquad h_2 = 3h_1\,.\]
Объём цилиндра \(C_1\) равен \(\pi ^2 h_1 = 4\pi ^2 h_1\) , а объём цилиндра \(C_2\) равен \(3\pi ^2 h_1\) , тогда \[\dfrac > > = \dfrac ^2 h_1> ^2 h_1> = 0,75\]
Объем цилиндра равен \(64\pi\) , а площадь боковой поверхности равна \(32\pi\) . Найдите площадь полной поверхности цилиндра, деленную на \(\pi\) .
Формулы для нахождения объема и боковой поверхности цилиндра: \(V = \pi R^2 h\) , \(S_ > = 2\pi R h\) . Зная величину объема и боковой поверхности, можно выразить радиус цилиндра: \[\frac >> = \frac = \frac = \frac = 2\] \(\Rightarrow\) \(R = 4\) . Площадь полной поверхности складывается из площади боковой поверхности и площадей двух оснований: \[S_ > = 2\pi R h + 2 \pi R^2 = 32\pi + 2 \cdot 16\pi = 64\pi.\] Осталось разделить полученный объем на \(\pi\) , тогда окончательно получаем \(64\) .
Объем цилиндра равен \(100\pi\) , а площадь боковой поверхности равна \(25\pi\) . Найдите высоту цилиндра.
Формулы для нахождения объема и боковой поверхности цилиндра: \(V = \pi R^2 h\) , \(S_ > = 2\pi R h\) . Зная величину объема и боковой поверхности, можно выразить радиус цилиндра: \[\frac >> = \frac = \frac = \frac = 4\] \(\Rightarrow\) \(R = 8\) . Подставим значение радиуса в формулу объема и найдем из этой формулы искомую высоту: \[V = \pi R^2 h = 64\pi h = 100\pi\] \(\Rightarrow\) \(\displaystyle h = \frac = 1,5625\) .
Объём цилиндра \[V = \dfrac >,\] а отношение радиуса его основания к его высоте равно \(5\) . Найдите площадь полной поверхности этого цилиндра.
\[V_ > = \pi R^2 H = \dfrac >,\] \(\dfrac = 5\) , где \(R\) – радиус основания цилиндра, \(H\) – его высота, тогда \(R = 5H\) , следовательно, \[\pi \cdot 25 H^3 = \dfrac >\qquad\Rightarrow\qquad H^3 = \dfrac >,\] откуда \(H = \dfrac >\) , \(R = \dfrac >\) . \[S_ > = 2\pi R H + \pi R^2 = 2\pi R(H + R) = 2\pi\cdot\dfrac >\cdot\dfrac > = 240.\]
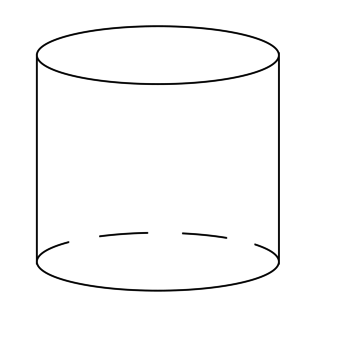
\(AD\) – ось цилиндра, \(BC\) – его образующая, \(S_ = \dfrac > >\) , \(\angle CAD = 60^\circ\) . Найдите объём цилиндра.
Читайте также: Шток рабочего цилиндра сцепления мазда 6 gg
Так как \(AD\) и \(BC\) – высоты цилиндра, то \(ABCD\) – прямоугольник, тогда \[S_ = AD\cdot DC = H\cdot R = \dfrac > >.\]
Рассмотрим прямоугольный треугольник \(ADC\) :
Т.к. \(\angle DAC = 60^\circ\) , то \[AD = \mathrm \, \angle ACD\cdot DC = \mathrm \, 30^\circ\cdot R = \dfrac >,\] т.е. \(H = \dfrac >\) или \(R = \sqrt H\) .
Повторение базовой теории и формул, в том числе и тех, которые позволяют выполнить расчет объема цилиндра, — один из основных этапов подготовки к ЕГЭ. Несмотря на то, что эта тема достаточно подробно рассматривается на уроках математики в школе, с необходимостью вспомнить основной материал и «прокачать» навык решения задач сталкиваются многие учащиеся. Понимая, как вычислить объем и другие неизвестные параметры цилиндра, старшеклассники смогут получить достаточно высокие баллы по итогам сдачи единого государственного экзамена.
Видео:Видеоурок по математике "Цилиндр"Скачать
Основные нюансы, которые стоит вспомнить
Чтобы вопрос, как посчитать объем цилиндра и выполнить измерение других неизвестных параметров при решении задач, не ставил ученика в тупик, рекомендуем повторить основные свойства этой фигуры прямо сейчас в режиме онлайн.
- Цилиндр представляет собой тело, которое ограничено цилиндрической поверхностью и двумя кругами. Цилиндрическая поверхность является боковой. А круги представляют собой основания фигуры.
- Высота цилиндра есть расстояние между плоскостями его оснований.
- Все его образующие являются параллельными и равными между собой.
- Радиус цилиндра есть радиус его основания.
- Фигура называется прямой, если ее образующие перпендикулярны основаниям.
Видео:Как найти объем. Принцип Кавальери | Ботай со мной #050 | Борис Трушин |Скачать
Как подготовиться к экзамену качественно и эффективно?
Занимаясь накануне прохождения аттестационного испытания, многие учащиеся сталкиваются с проблемой поиска необходимой информации. Далеко не всегда школьный учебник оказывается под рукой, когда это требуется. А найти формулы, которые помогут рассчитать площадь и другие неизвестные параметры цилиндра, часто бывает достаточно сложно даже в Интернете в онлайн-режиме.
Занимаясь вместе с математическим порталом «Школково», выпускники смогут избежать типовых ошибок и успешно сдать единый госэкзамен. Мы предлагаем выстроить процесс подготовки по-новому, переходя от простого к сложному. Это позволит учащимся определить непонятные для себя тематики и ликвидировать пробелы в знаниях.
Весь базовый материал, который поможет в решении задач на тему «Цилиндр», выпускники смогут найти в разделе «Теоретическая справка». Специалисты «Школково» изложили с доступной форме все необходимые определения и формулы.
Для закрепления полученных знаний учащиеся могут попрактиковаться в решении задач на тему «Цилиндр» и другие темы, например, нахождение площади или объема конуса. Большая, постоянно обновляющаяся подборка заданий представлена в разделе «Каталог».
Чтобы во время подготовки к ЕГЭ быстро найти конкретную задачу по теме «Цилиндр» и освежить в памяти алгоритм ее решения, выпускники могут предварительно сохранить ее в «Избранное». Отрабатывать собственные навыки на нашем сайте имеют возможность не только столичные школьники, но и учащиеся из других российских городов.
💡 Видео
Пересечение двух цилиндров: объем и площадь поверхности через двойной интегралСкачать
11 класс, 32 урок, Объем цилиндраСкачать
Урок 4 - объем, мощность, крутящий момент, расход топлива двигателя, малолитражки, крупнолитражки.Скачать
Объем и площадь поверхности цилиндра (видео 44) | Подобие. Геометрия | МатематикаСкачать
Объем цилиндра. Практическая часть. 11 класс.Скачать
Объем цилиндра.Скачать
Миникурс по геометрии. Куб, призма, цилиндр и конусСкачать
Стереометрия. ЕГЭ. Дано два цилиндра. Найдите объём второго цилиндраСкачать
Тихо и без лишнего шума: Россия стала страной-двигателеколонкойСкачать
11 класс, 15 урок, Площадь поверхности цилиндраСкачать
Объем цилиндра.Скачать
Как работает двигатель внутреннего сгорания автомобиля?Скачать
РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать
ЕГЭ по математике. Базовый уровень. Задание 13. Объем цилиндра.Скачать
