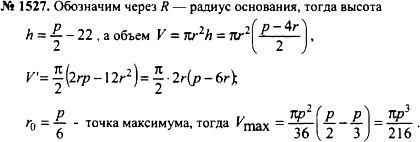PDF-файл из архива «Г.Н. Берман — Сборник задач с ответами», который расположен в категории «книги и методические указания». Всё это находится в предмете «математическое моделирование» из девятого семестра, которые можно найти в файловом архиве МГТУ им. Н.Э.Баумана. Не смотря на прямую связь этого архива с МГТУ им. Н.Э.Баумана, его также можно найти и в других разделах. Архив можно найти в разделе «книги и методические указания», в предмете «математическое моделирование» в общих файлах.
- Просмотр PDF-файла онлайн
- Текст 3 страницы из PDF
- Найдем объем цилиндра. ГДЗ 10 класс алгебра Алимов Упражнения для повторения № 1527
- производная егэ презентация к уроку по геометрии (11 класс) на тему
- Скачать:
- Предварительный просмотр:
- Подписи к слайдам:
- По теме: методические разработки, презентации и конспекты
- 🎥 Видео
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Просмотр PDF-файла онлайн
Видео:Видеоурок по математике "Цилиндр"Скачать

Текст 3 страницы из PDF
66. В сосуд произвольной формы налита жидкость. На глубине й 25,3 см давление втой жидкости р = 1,84 10а Па. а) Составить функцию, выражающую зависимость давления от алубины. б) Определить давление на глубине и = 14,5 см. в) На какой глубине давление станет равным 2,65 10з Пау 67. Тело движется прямолинейно под действием силы Е. Исходя из закона Ньютона, написать функцию, выражающую зависимость между силой Р и ускорением в„если известно, что если тело движется с ускорением 12 м7с’, то на пути а=15 м производится работа А =32 Дж. 68. Определить линейную функцию д ах+Ь по следующим 4 з, пвостаишиа фхнкцин 69. Некоторое количество газа занимало при 20 ‘С объем 107 смэ, при 40’С объем стал равным 114 см’. а) Составить, исходя из закона Гей-Люссака, функцию, выра.
жающую зависимость объема к» газа от температуры й б) Каков будет объем при 0’Се 70. Равномерно движущаяся по прямой точка через 12 с ноэле начала движения находилась иа расстоянии + 32,7 см от некоторой точки этой прямой; через 20 с после начала движения расстояние стало равным +43,4 см. Выразить расстояние э как функцию вре- мени д 7!. Напряжение в некоторой цепи падает равномерно (по линей- ному закону). В начале опыта напряжение было равно 12 В, а по окончании опыта, длившегося 8 с, напряжение упало до 6,4 В.
Выразить напряжение )г как функцию времени ! и построить график втой функции. 72. Найти приращение линейной функции у = 2х — 7 прн пере- ходе независимой переменной х от значения х, =3 к значению хз — — 6. 73. Найти приращение линейной функции у= — Зх+1, соот- ветствующее приращению независимой переменной йх = 2. 74. Функция у=2,5х+4 получила приращение бр=10. Найти прн ращение аргумента. 7$. Даны функция у= — ‘, ‘, и начальное значение независи- мой переменной хг=а — Ь. При каком конечном значении хэ не- 1 зависимой переменной х приращение Ау= — ? а — Ь 76.
Видео:Задание №607 — ГДЗ по геометрии 11 класс (Атанасян Л.С.)Скачать

Найдем объем цилиндра. ГДЗ 10 класс алгебра Алимов Упражнения для повторения № 1527
Приветик, решим?
Из всех цилиндров, у которых периметр осевого сечения равен р, выбран цилиндр наибольшего объёма. Найти этот объём.
Решим конечно.
Вот уж не думала, что не справлюсь( Но что то никак не сходиться, спасайте! Вот условие:
Найти тангенс угла, который касательная к ( Подробнее. )
Привет. Выручайте с ответом по математике…
Найдите значение выражения ( Подробнее. )
Привет всем! Нужен ваш совет, как отвечать…
Найдите значение выражения 3,12 : 2,6-0,8.
Читайте также: Главный цилиндр сцепления 2101 фенокс
в одном из ядерных экспериментов протон с энергией в 1МэВ движется в однородном магнитном поле по круговой траектории. какой энергией ( Подробнее. )
Замените значок * таким выражением, чтобы выполнялось равенство:
1) (*)5 = a25; 2) (*)2 = а10; 3) (*)3 = а3n; 4) (*)n = ( Подробнее. )
Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

производная егэ
презентация к уроку по геометрии (11 класс) на тему
Видео:РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать

Скачать:
Как сдать ЕГЭ на 80+ баллов?
Репетиторы Учи.Дома помогут подготовиться к ЕГЭ. Приходите на бесплатный пробный урок, на котором репетиторы определят ваш уровень подготовки и составят индивидуальный план обучения.
Бесплатно, онлайн, 40 минут
Предварительный просмотр:
Видео:№525. Площадь осевого сечения цилиндра равна 10 м2, а площадь основания — 5 м2.Скачать

Подписи к слайдам:
Производная и ЕГЭ Авторы: Емельянова Р.Н.
Цель исследования Устранить некоторые противоречия между уровнем подготовки ученика средней школы в соответствии с программой по математике и требованиями, предъявляемыми к абитуриенту при поступлении в ВУЗы по теме «Применение производной к решению задач».
Задачи исследования Проанализировать задания КИМов ЕГЭ по теме «Производная». Выделить группы заданий по данной теме. Определить пути решения данных заданий. Познакомить учащихся с вариантами решений данных заданий. Закрепить знания учащихся по данной теме Мотивировать самостоятельную исследовательскую деятельность учащихся.
Актуальность исследования Решение геометрических задач на нахождение наибольшего и наименьшего значения площади вызывает затруднения у школьников, а между тем они все чаще встречаются на школьных экзаменах ЕГЭ и на вступительных экзаменах в ВУЗах, поэтому эта проблема актуальна для учащихся.
Аннотация Проанализировав задания КИМов, мы пришли к выводу, что геометрические задачи группы С представляют для учащихся большую трудность так как учебные программы общеобразовательной школы не предполагают углубленного изучения и отработки навыков решения задач по теме «Применение производной к решению геометрических задач». Мы выделили две группы задач: 1) на нахождение наибольшего и наименьшего значения площади сечения; 2) решение задач на комбинацию геометрических тел. Важным при решении задач такого типа являются: правильное построение геометрического тела и его сечения; использование алгоритма нахождения наибольшего и наименьшего значений функции.
Задача 1 . В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 с ребрами CD = 24, AD = 6 и DD 1 =4 проведена плоскость через центр симметрии грани A 1 B 1 C 1 D 1 , вершину А и точку Р, лежащую на ребре DC . Какую наименьшую площадь может иметь сечение параллелепипеда этой плоскостью? На какие части делит точка P ребро DC в этом случае? Решение. Проведем плоскость и построим сечение (рис.). АО АA 1 C 1 С — линия, принадлежащая данной плоскости. Продолжим АО до пересечения с CC 1 в точке S. Тогда SP — линия пересечения грани DD 1 C 1 C и данной плоскости, а сечение ANMP — параллелограмм. Sсеч = SAMNP = SK*AP/2 , потому что SK/2— высота параллелограмма ANMP. Это видно из следующего рассуждения. В ΔASC ОC 1 — средняя линия (значит SC 1 = 4), в ΔPSC также средняя линия МC 1 , а плоскость A 1 B 1 C 1 D 1 делит пополам любую линию между S и плоскостью ABCD, а значит и SK. A B D P A 1 C K L S M N O D 1 C 1 B 1 24 6 4 A 1 C 1 C A O S 4 4 D C B A 24-x L P x K
Пусть PC = x ; Δ CLP подобен Δ D AP , LC/AD = x/(24—x), LC = 6x/(24— x); _____________ ____________ Из Δ CLP: KC = (6x*x/(24—x))/(√(36×2/(24—x)2)+x2) = 6x/(√(36+ (24—x)2); ________ ___________________ __________________ Из Δ SCK: SK = √ SC2+ KC2 = √64+36×2/(36+(24—x)2) = 2√16+9×2/(36+(24—x)2) ; Из Δ ADP : AP = √36+(24 — x )2; _________ _________________ __________________ Sсеч = AP * SK /2 = 0,5*(√36+(24— x )2) 2√16+9 x 2/(36+(24— x )2) = √16(36+(24— x )2)+9 x 2; Если S ’( x ) = 0, то 18 x +16*2(24— x )(-1) = 0; 50 x —32*24 = 0, x = 32*24/50 = 32*12/25 = 384/25 (это точка min ); Sсеч = 312; DP = 24—16*24/25 = 216/25; Ответ: 312 кв. ед.; DC : 384/25; 216/25.
Задача 2 . Высота пирамиды TABC с основанием ABC проходит через середину ребра AC. Выберите на AC точку М так, чтобы площадь сечения пирамиды плоскостью, проходящей через точку M, середину ребра TC и вершину B, была наименьшей, если AB=BC=AC=TC=2. Решение. HF=FC=1/2; S∆BME = BM*EK*1/2; Из ∆TCH => TH = √4—1=√3; EF = TH/2=√3/2; Пусть MC = x. Из ∆BMC по теореме косинусов MB2= x2+4—2*2*x*1/2; MB = √x2—2x+4; S∆BMC = 0,5*MC*BC*sinC=(x/2)*2√3 /2 = x√3/2; S∆BMC = 0,5*BM*PC, PC = (2S∆BMC)/BM, PC = x√3/√x2—2x+4 ; ∆ KMF подобен ∆PMC(по двум углам): KF/PC = MF/MC(рис 2), KF = x√3(x—1/2)/(x√x2—2x+4) = √3(x—1/2)/(√x2—2x+4); Из ∆KEF => KE = √ KF2+EF2 = √3(x—1/2)2/(x2—2x+4)+3/4; S∆BME = 0,5√x2—2x+4 *√3(x—1/2)2/(x2—2x+4)+3/4 = 0,5√3(x—1/2)2+(x2—2x+4)*3/4; Если S’(x) = 0, то 6(x—1/2)+(2x—2)*3/4 = 0; 15x—9 = 0; x = 3/5; S(3/5) = √15/5 кв.ед. Ответ: √15/5 кв.ед. A B C K M H E T F A B M F C K P
Читайте также: Как менять заглушку в блоке цилиндров
Задача 3 . В сферу радиусом R вписана правильная треугольная пирамида, у которой боковое ребро образует с высотой пирамиды угол 60o. Какую наименьшую площадь может иметь треугольник MBK, если точка M лежит на апофеме пирамиды, а BK — высота основания пирамиды, не пересекающая апофему? Решение. TP = 2R, ATO = 60 градусов. O K A T P C D L N M Пусть AB = BC = CA = a(рис.) Тогда AO = a√3/3, AD = BK = a√3/2, TO = AO*ctg60o= a√3/3*1/√3 = a/3, OD = a√3 /6, AO2 = TO*OP = TO(2R — TO), a2/3 = a(2R – a/3)/3, a = 3R/2. S∆MBK = BK*LM*1/2, BK = const, S∆MBK = f(LM), LM = √MN2+NL2 Пусть MD = x, тогда MN = x cos / NMD;
cos NMD = TO/TD = a/(3√a2/9+a2/12 = 2/√7, MN = 2x/√7 . Из ∆ONL: LN = ON cos30o (ONL = 30o); ON = OD – ND, ND = x sin NMD = x √3/√7, ON = a√3/6 — x√3/√7, LN = (a√3/6 — x√3/7)√3/2 = (a/4 – 3x/(2√7)), LM = √4×2/7+(a/4 – 3x/(2√7))2. Если LM’(x) = 0, то 8x/7+2(a/4 – 3x/(2√7))(-3/2√7) = 0, 8x/7 – 3a/4√7 + 9x/14 = 0, 25x/14 = 3a/4√7, x = 21a/50√7. MN = (21a/50√7)*(2/√7) = 3a/25, LN = a/4 – (3/2√7)*(21a/50√7) = 4a/25, LM = √a2/625 + 9a2/625 = a√10/25. _ S∆MBK = a√3/2*a/5*1/2 = a√3/20 = 9√3 R2/80. Ответ: : 9√3 R2/80.
Задача 4 . В сферу радиусом R вписана правильная треугольная пирамида, высота которой в 1,5 раза меньше высоты основания. Между боковой гранью пирамиды и сферой расположена правильная четырехугольная призма, одно из оснований которой (ближнее к центру сферы) лежит в плоскости боковой грани пирамиды, а вершины другого основания принадлежат сфере. Какой должна быть высота призмы, чтобы ее объем был наибольшим? Найти этот объем. Решение. SABC – правильная треугольная пирамида (рис), вписанная в сферу радиусом R, SO*1,5 = AD, LMN – правильная четырехугольная призма. Найти. Vпр = f(LM). Пусть SO = H, тогда AD = 1,5H; SO1 = R – радиус сферы; LM = x –высота призмы. ∆ SKO1 подобен ∆SOD => O1K/OD = SO1/SD => OK1 = OD*SO1/SD. Из ∆AO1O: R2 = AO2 + O1O2 = (2AD/3)2 + (AD*2/3 — R)2, R2 = 4AD2/9 + 4AD2/9 –AD*R*4/3, 8AD2/9 = AD*R*4/3 => AD = 3R/2. Отсюда OD = R/2; AO1 = R и SO1 = R; _ SD = √R2 + R2/4 = R√5/2, _ OK1 = 2*R*R/(2R√5) = R√5/5; A S B C L O M N D P O 1 K F
O1K = R√5/5. Из ∆O1FN => R2 = (O1K + x)2 + NF2, NF = √R2 – R2/5 – 2x(√5)2/5 – x2 , Sосн = 2NF2. Vпр = Sосн*x = 2(R2 – R2/5 – 2x√5 R/5 — x2)*x; Vпр = 2(4R2x/5 – 2×2√5 R/5 — x3); V’пр(x) = 2(4R2/5 – 2x√5 R/5 — 3×2) = 0; X 1,2 = (2R√5/5 + √4R2/5 + 12R2/5)/(-3) = (2R√5/5 + 4R/√5)/(-3); X = 2√5 R/15 Vпр.max = 2(4R2*2√5R/(5*15) – 2√5R*4R2/(45*5) — 40√5R3/(225*15)) = 16R3√5(1 – 1/3 – 5/45)/75 = 16√5R3/135. Ответ: 16√5R3/135 м3 при H = 2√5R/15.
Задача 5 . В конус вписан цилиндр, одно из оснований которого лежит в плоскости основания конуса, а окружность другого основания принадлежит боковой поверхности конуса. Правильная четырехугольная призма расположена так, что ее. нижнее основание лежит в плоскости верхнего основания цилиндра, вершины верхнего основания принадлежат боковой поверхности конуса. Отношение длины диагонали основания призмы к ее высоте равно отношению длины диаметра цилиндра к его высоте. При какой высоте цилиндра объем призмы будет наибольшим? Найти этот объем призмы, если высота конуса – H и радиус основания – R. Дано. ASO – конус; SO = H; AO = R; CL/CM = BK/BN; Найти. BN, чтобы Vпр = max S D C L B M A N O K h x E
Читайте также: Хлопки в цилиндре мотоцикла
Решение. BN = x, CM = h, Vпр = Sосн CM = CL2h/2. ∆ CSD подобен ∆ASO: CD/AO = SD/SO; CD/R = (H – x — h)/H; CD = R(H – x -h)/H. ∆ BSE подобен ∆ASO: BE/AO = SE/SO; BE/R = (H — h)/H; BE = R(H — h)/H. Находим отношение CD/BE = (H – x — h)/(H — x). Исходя из условия (CL/CM = BK/BN) задачи делаем вывод, что CD/BE = h/x, т. е. (H – x — h)/(H — x) = h/x => h = (Hx – x2)/H Тогда CD = R(H – x – (Hx – x2)/H)/H = R(H2 – Hx – Hx +x2)/H2 = R(H — x)2/H2, CL = 2CD = 2R(H — x)2/H2. V = 4R2(H — x)4(H — x)x/(2H*H4) = 2R2(H — x)5x/H5; V’(x) = 2R2((H — x)5 – 5(H — x)4 x)/H5 = 0, (H – x) – 5x = 0, x = H/6. V = 2HR^2(5H/6)^5/(6H^5) = 2(R^2)H*(5 ^ 5)/(6^6). Ответ: при H/6, Vmax = 2 ( R ^ 2 ) H* ( 5^5 ) / ( 6 ^ 6 ) . H/6 x
Задачи для самостоятельного решения Приведение в систему знаний можно с успехом проводить с помощь специально подобранных задач самостоятельного решения. Апофема правильной четырехугольной пирамиды равна p . При какой высоте пирамиды ее объем будет наибольшим. . База находится в лесу в 5 км от дороги, а в 13 км от базы на этой дороге есть железнодорожная станция. Пешеход по дороге идет со скоростью 5 км/ч, а по лесу 3 км/ч. За какое минимальное время пешеход может добраться от базы до станции? . Открытый металлический бак с квадратным основанием должен вмещать 32 л воды. При каких размерах на его изготовление уйдет наименьшее количество материала? . Периметр осевого сечения цилиндра равен p см. Какова должна быть высота цилиндра, чтобы его объем был наибольшим? . Закрытый металлический бак с квадратным дном должен иметь объем 343 . При каких размерах на его изготовление пойдет наименьшее количество материала? . Учащимся предлагается найти самостоятельные способы рещения задач, наиболее интересные решения обсуждаются в классе. Лучшие работы отмечаются грамотами.
Вывод Данное исследование позволяет расширить знания учащихся по теме «Производная», закрепить навыки решения задач по нахождению наибольшего и наименьшего значения функции, мотивировать самостоятельную исследовательскую деятельность учащихся, заинтересовать их результатом учебной деятельности, научить применять полученные знания в практической деятельности (подготовка к ЕГЭ).
Видео:11 класс, 27 урок, Сечения цилиндрической поверхностиСкачать

По теме: методические разработки, презентации и конспекты
Проверочная работа по теме «Производная сложной функции. Производная тригонометрических функций».Работа содержит формулы, которые, к сожалению, не видны в разделе предпросмотр.
Урок соответствует технологии модульного обучения.
Урок обобщающего повторения по теме:« Геометрический и физический смысл производной. Применение производной». Урок сопровождается презентацией.
Урок обобщения и систематизации знаний. Осуществляется подготовка к ЕГЭ по заданиям с производной. Используются различные формы работы (фронтальная, групповая, самостоятельная работа учащихся).
Урок обобщения и закрепления знаний по теме. 10 класс .
Зачет имеет большое обучающее и воспитывающее значение для учащихся.В вечерней школе зачеты проводятся после каждой большой темы или раздела программы. Подготовка к зачетам должна начинаться с п.
Данная проверочная работа может быть использована как для проверки знаний после окончания прохождения темы, так и в ходе итогового повторения при подготовке к ЕГЭ. Работа составлена .
🎥 Видео
11 класс, 15 урок, Площадь поверхности цилиндраСкачать

ТЕМА 3. ПРИНЦИПЫ ПЕРЕСЕЧЕНИЯ ЦИЛИНДРА И ШАРА С ПРЯМЫМИ ПЛОСКОСТЯМИСкачать

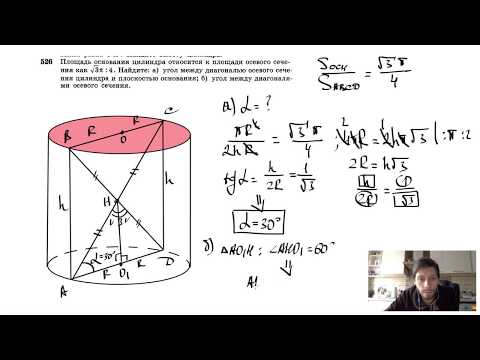
№526. Площадь основания цилиндра относится к площади осевого сечения как √3π:4. Найдите:Скачать
Построение линии пересечения поверхности цилиндра с проецирующей плоскостиСкачать

Профильный ЕГЭ 2024. Вся стереометрия первой части. Задача 3. МиниСИРОПСкачать

№523. Осевое сечение цилиндра — квадрат, диагональ которого равна 20 см. Найдите: а) высотуСкачать

№545. Цилиндр получен вращением квадрата со стороной а вокруг одной из его сторон.Скачать

11 класс, 18 урок, Усеченный конусСкачать

11 класс, 32 урок, Объем цилиндраСкачать

Миникурс по геометрии. Куб, призма, цилиндр и конусСкачать

Призма и цилиндр. Практическая часть. 11 класс.Скачать

11 класс, 14 урок, Понятие цилиндраСкачать

ЕГЭ-2022. ЯЩЕНКО. 36-ВАРИАНТОВ. ЗАДАНИЕ-5, СТЕРЕОМЕТРИЯСкачать