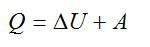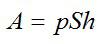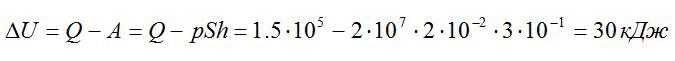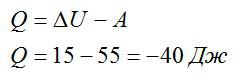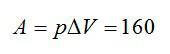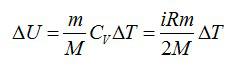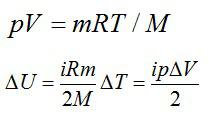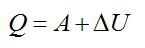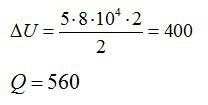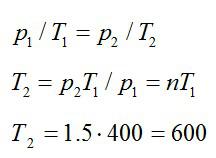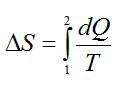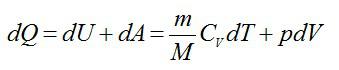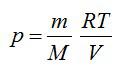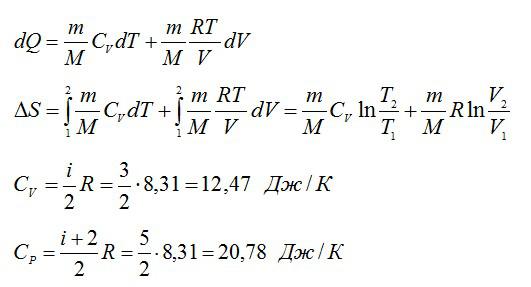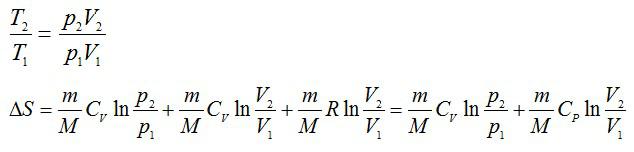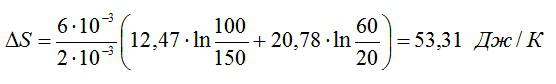Изменение внутренней энергии газа в цилиндре

2017-10-13
В расположенном горизонтально цилиндре (рис. 1) слева от закрепленного поршня находится идеальный газ, в правой части цилиндра — вакуум. Цилиндр теплоизолирован от окружающей среды, а пружина, расположенная между поршнем и стенкой, находится первоначально в недеформированном состоянии. Поршень освобождают, и после установления равновесия объем, занимаемый газом, увеличивается вдвое. Как изменились при этом температура и давление газа? Теплоемкостями цилиндра, поршня и пружины пренебречь.

По условию задачи вначале пружина находится в Heдеформированном состоянии и сила давления газа на поршень уравновешивается упором, удерживающим поршень. Когда упор убирают, поршень под действием давления газа перемещается вправо и сжимает пружину. По инерции поршень проскакивает положение равновесия, и сжатая пружина после остановки толкает его обратно. В системе возникают колебания, которые вследствие трения постепенно затухают, и поршень останавливается в положении равновесия. В начальном состоянии вся энергия рассматриваемой системы состояла только из внутренней энергии газа, ибо поршень был неподвижен, а пружина не деформирована. В конечном состоянии энергия системы складывается из внутренней энергии газа и потенциальной энергии сжатой пружины. В процессе установления равновесия происходили многократные превращения энергии из одного вида в другие: внутренняя энергия газа частично превращалась в кинетическую энергию макроскопического движения газа в цилиндре вслед за поршнем, в кинетическую энергию поршня, потенциальную энергию деформированной пружины и обратно.

В процессе колебаний вследствие трения механическая энергия превращалась в теплоту, т. е. во внутреннюю энергию газа. Изменением внутренней энергии поршня, стенок сосуда и пружины можно пренебречь, так как по условию задачи их теплоемкость мала по сравнению с теплоемкостью газа. На основании первого закона термодинамики можно утверждать, что полная энергия системы в результате всех этих процессов не изменилась, так как теплообмен с окружающей средой отсутствовал и система не совершала механической работы над внешними телами.

Сохранение полной энергии системы выражается соотношением

где второе слагаемое есть потенциальная энергия пружины жесткости $k$, сжатой на величину $x$, а изменение внутренней энергии идеального газа при изменении его температуры от $T_ $ до $T_ $ равно

где $\nu = m / \nu$ — количество газа в цилиндре, а $C_ $ — молярная теплоемкость идеального газа при постоянном объеме.

В положении равновесия сила давления газа на поршень площади $S$ уравновешивается силой реакции сжатой пружины:

Смещение поршня $x$ очевидным образом связано с изменением объема газа от $V_ $ до $V_ $:

Подставив в уравнение баланса энергии (1) выражения (2) и (4), получим

Используя уравнение состояния идеального газа

Выразим давление газа $p_ $ в условии механического равновесия поршня (3) через конечные значения температуры и объема, а смещение поршня $x$ — с помощью формулы (4):

Разделив почленно выражения (5) и (7), получим

При заданном отношении начального и конечного объемов газа формула (8) дает возможность определить отношение температур:

Зная, отношение объемов и температур, можно с помощью уравнения состояния (6) найти отношение давлений:

Поскольку для идеального одноатомного газа $C_ = 3R/2$, а по условию задачи конечный объем вдвое больше начального, то с помощью формул (9) и (10) находим

Читайте также: Замена прокладки блока цилиндров ваз 2109 карбюратор

Полученные формулы (9) и (10) полезно проверить для предельного случая, когда ответ очевиден. Если жесткость пружины $k \rightarrow \infty$, то газ не сможет сдвинуть поршень с места, и, следовательно, объем, температура и давление газа останутся без изменения. В этом случае $V_ = V_ $ и формулы (9) и (10), как и полагается, дают $T_ = T_ $ и $p_ = p_ $.

Видео:Внутренняя энергия. Способы изменения внутренней энергии. 8 класс.Скачать

Задачи на первый закон термодинамики с решениями

Первый закон, или первое начало термодинамики является частным случаем закона сохранения энергии. Разберемся, как он работает, с помощью решения простых задач. Кстати, у нас есть и примеры решения задач на второе начало термодинамики.

Подписывайтесь на наш телеграм-канал, чтобы не только легко решать задачи, но и узнавать лайфхаки для любых жизненных ситуаций.

Видео:Урок 166. Предмет термодинамики. Внутренняя энергия телаСкачать

Первый закон термодинамики: решение задач

Алгоритм решения задач на первый закон термодинамики ничем не отличается от алгоритма решения любой другой физической задачи. С ним вы можете ознакомиться, открыв нашу универсальную памятку. Также полезно будет держать под рукой формулы, которые часто используются при решении задач.

Задача №1. Применение первого закона термодинамики

Газ находился в цилиндре с поршнем площадью поперечного сечения 200 см^2. После того, как газ нагрели, сообщив ему количество теплоты в 1,5*10^5 Дж, поршень сдвинулся на расстояние h=30 см. Как изменилась внутренняя энергия газа, если его давление осталось равным 2*10^7 Па.

Запишем первое начало термодинамики:

Работу против внешних сил, которую совершил газ, можно найти по формуле из механики:

Ответ: 30 кДж.

Задача №2. Применение первого закона термодинамики

Над газом была совершена работа 55 Дж, а его внутренняя энергия увеличилась на 15 Джоулей. Какое количество теплоты получил или отдал газ в этом процессе?

Записываем первое начало термодинамики и подставляем значения:

A пишется со знаком «минус», так как это работа внешних сил над газом, а не наоборот.

Ответ: в процессе газ отдал 40 Дж теплоты.

Задача №3. Расчет работы, изменения внутренней энергии и количества теплоты

Кислород нагрели при постоянном давлении p=80 кПа. Объем газа увеличился с 1 до 3 кубических метров. Определить изменение внутренней энергии кислорода, работу, совершенную газом, и количество теплоты, сообщенное ему.

Изменение внутренней энергии равно:

Используем уравнение состояния газа:

Число степеней свободы i для двухатомной молекулы равно 5.

Согласно первому закону термодинамики, сообщенное газу тепло равно:

Ответ: А=160 кДж, ∆U=400 кДж, Q=560 кДж.

Задача №4. Изопроцессы

Газ находится в баллоне при температуре 400 К. До какой температуры нужно нагреть газ, чтобы его давление увеличилось в 1,5 раза?

Так как нагревание газа происходит при постоянном объеме, процесс – изохорный. При изохорном процессе:

Ответ: 600 К.

Задача №5. Расчет изменения энтропии

Найти изменение ∆S энтропии при расширении массы m = 6 г гелия от объема V1 = 20 л под давлением р1 = 150 кПа к объему V2 = 60 л под давлением р2 = 100 кПа.

Изменение энтропии при переходе вещества из состояния 1 в состояние 2:

Согласно первому началу термодинамики:

Из уравнения Менделеева-Клапейрона выразим давление:

Из уравнения Менделеева-Клапейрона:

Кстати! Для наших читателей действует скидка 10% на любой вид работы.

Видео:Физика 10 класс (Урок№23 - Внутренняя энергия. Работа. Количество теплоты.)Скачать

Вопросы по теме «1-ый закон термодинамики»

Вопрос 1. Приведите пример действия первого закона термодинамики.

Ответ. В качестве примера можно привести газ в сосуде. Если сообщить ему какое-то количество теплоты, оно пойдет на увеличение внутренней энергии газа в сосуде.

Вопрос 2. Сформулируйте первый закон термодинамики.

Ответ. В любой изолированной системе запас энергии остается постоянным.

Вопрос 3. Как еще можно сформулировать первый закон термодинамики?

Ответ. Вот разные формулировки первого закона термодинамики:

1. Количество теплоты, полученное системой, идет на изменение внутренней энергии системы, а также на совершение работы против внешних сил.
2. Невозможен вечный двигатель первого рода (двигатель, совершающий работу без затраты энергии).

Читайте также: Радиус основания цилиндра 8 высота 5 найти площадь осевого сечения

Вопрос 4. Что такое изопроцесс? Какие есть изопроцессы?

Изопроцесс – это термодинамический процесс, при котором один из параметров системы (давление, объем, температура, энтропия) остается неизменным.

• изотермическим (T=const);
• изобарным (P=const);
• изохорным (V=const);
• Адиабатическим (отсутствует теплообмен с окружающей средой).

Вопрос 5. При каком изопроцессе газ не совершает работу?

Ответ. При изохорном.

Ищете, где почитать теорию по теме, а учебника нет под рукой? Далеко ходить на надо, почитайте наш отдельный материал по первому началу термодинамики. А если при решении заданий понадобится помощь, обращайтесь в профессиональный студенческий сервис.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Видео:Газ под поршнем в цилиндре с клыкамиСкачать

Первый закон термодинамики

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.

Начнём с обсуждения работы газа.

Газ, находящийся в сосуде под поршнем, действует на поршень с силой , где — давление газа, — площадь поршня. Если при этом поршень перемещается, то газ совершает работу.

При расширении газа эта работа будет положительной (сила давления газа и перемещение поршня направлены в одну сторону). При сжатии работа газа отрицательна (сила давления газа и перемещение поршня направлены в противоположные стороны).

Видео:Внутренняя энергия. 10 класс.Скачать

Работа газа в изобарном процессе

Предположим, что газ расширяется при постоянном давлении . Тогда сила , с которой газ действует на поршень, также постоянна. Пусть поршень переместился на расстояние (рис. 1 ).

Но — изменение объёма газа. Поэтому для работы газа при изобарном расширении мы получаем формулу:

Если и — начальный и конечный объём газа, то для работы газа имеем: . Изобразив данный процесс на -диаграмме, мы видим, что работа газа равна площади прямоугольника под графиком нашего процесса (рис. 2 ).

Рис. 2. Работа газа как площадь

Пусть теперь газ изобарно сжимается от объёма до объёма . С помощью аналогичных рассуждений приходим к формуле:

Но , и снова получается формула (1) .

Работа газа опять-таки будет равна площади под графиком процесса на -диаграмме, но теперь со знаком минус.

Итак, формула выражает работу газа при постоянном давлении — как в процессе расширения газа, так и в процессе сжатия.

Видео:Внутренняя энергия | Физика 10 класс #38 | ИнфоурокСкачать

Работа газа в произвольном процессе

Геометрическая интерпретация работы газа (как площади под графиком процесса на -диаграмме) сохраняется и в общем случае неизобарного процесса.

Действительно, рассмотрим малое изменение объёма газа — настолько малое, что давление будет оставаться приблизительно постоянным. Газ совершит малую работу . Тогда работа газа во всём процессе найдётся суммированием этих малых работ:

Но данный интеграл как раз и является площадью криволинейной трапеции (рис. 3 ):

Рис. 3. Работа газа как площадь

Видео:Работа при расширении газа (часть 4) | Термодинамика | ФизикаСкачать

Работа, совершаемая над газом

Наряду с работой , которую совершает газ по передвижению поршня, рассматривают также работу , которую поршень совершает над газом.

Если газ действует на поршень с силой , то по третьему закону Ньютона поршень действует на газ с силой , равной силе по модулю и противоположной по направлению: (рис. 4 ).

Рис. 4. Внешняя сила , действующая на газ

Следовательно, работа поршня равна по модулю и противоположна по знаку работе газа:

Так, в процессе расширения газ совершает положительную работу 0 \right )’ alt=’\left ( A> 0 \right )’/> ; при этом работа, совершаемая над газом, отрицательна . Наоборот, при сжатии работа газа отрицательна , а работа, совершаемая поршнем над газом, положительна 0 \right )’ alt=’\left ( ‘ > 0 \right )’/> .

Читайте также: Пружина рабочего цилиндра сцепления уаз буханка

Будьте внимательны: если в задаче просят найти работу, совершённую над газом, то имеется в виду работа .

Как мы знаем, существует лишь два способа изменения внутренней энергии тела: теплопередача и совершение работы.

Опыт показывает, что эти способы независимы — в том смысле, что их результаты складываются. Если телу в процессе теплообмена передано количество теплоты , и если в то же время над телом совершена работа , то изменение внутренней энергии тела будет равно:

Нас больше всего интересует случай, когда тело является газом. Тогда (где , как всегда, есть работа самого газа). Формула (2) принимает вид: , или

Соотношение (3) называется первым законом термодинамики. Смысл его прост: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа и на совершение газом работы.

Напомним, что величина может быть и отрицательной: в таком случае тепло отводится от газа. Но первый закон термодинамики остаётся справедливым в любом случае. Он является одним из фундаментальных физических законов и находит подтверждение в многочисленных явлениях и экспериментах.

Видео:Урок 167. Вычисление работы в термодинамикеСкачать

Применение первого закона термодинамики к изопроцессам

Напомним, что в изопроцессе остаётся неизменным значение некоторой величины, характеризующей состояние газа — температуры, объёма или давления. Для каждого вида изопроцессов запись первого закона термодинамики упрощается.

1. Изотермический процесс, .
Внутренняя энергия идеального газа зависит только от его температуры. Если температура газа не меняется, то не меняется и внутренняя энергия: . Тогда формула (3) даёт:

Всё подведённое к газу тепло идёт на совершение газом работы.

2. Изохорный процесс, .
Если объём газа остаётся постоянным, то поршень не перемещается, и потому работа газа равна нулю: . Тогда первый закон термодинамики даёт:

Всё тепло, переданное газу, идёт на изменение его внутренней энергии.

3. Изобарный процесс, .
Подведённое к газу тепло идёт как на изменение внутренней энергии, так и на совершение работы (для которой справедлива формула (1) ). Имеем:

Видео:Физика 10 класс Внутренняя энергия газа и ее изменениеСкачать

Адиабатный процесс

Процесс называется адиабатным, если он идёт без теплообмена с окружающими телами.

Адиабатный процесс совершается газом, находящимся в теплоизолированном сосуде. Такой сосуд препятствует всем видам теплопередачи: теплопроводности, конвекции, излучению. Пример теплоизолированного сосуда — термос.

Приблизительно адиабатным будет всякий процесс, протекающий достаточно быстро: в течение процесса теплообмен просто не успевает произойти.

При адиабатном процессе . Из первого закона термодинамики получаем: , или .

В процессе адиабатного расширения газ совершает положительную работу, поэтому (работа совершается за счёт убыли внутренней энергии). Следовательно, газ охлаждается. Если заставить газ совершить достаточно большую работу, охладить его можно весьма сильно. Именно на этом основаны методы сжижения газов.

Наоборот, в процессе адиабатного сжатия будет , поэтому 0′ alt=’\Delta U > 0′/> : газ нагревается. Адиабатное нагревание воздуха используется в дизельных двигателях для воспламенения топлива.

Кривая, изображающая ход адиабатного процесса, называется адиабатой. Интересно сравнить ход адиабаты и изотермы на -диаграмме (рис. 5 ).

Рис. 5. Сравнительный ход изотермы и адиабаты

В обоих процессах давление убывает с увеличением объёма, но в адиабатном процессе убывание идёт быстрее. Почему?

При изотермическом расширении давление падает потому, что уменьшается концентрация частиц газа, в результате чего удары частиц по стенкам сосуда становятся реже. Однако интенсивность этих ударов остаётся прежней: ведь температура газа не меняется — значит, не меняется и средняя кинетическая энергия его частиц.

А при адиабатном расширении, наряду с уменьшением концентрации частиц, падает также и температура газа. Удары частиц становятся не только более редкими, но и более слабыми. Вот почему адиабата убывает быстрее изотермы.

🔍 Видео

Как за 3 МИНУТЫ понять Физику — Внутренняя ЭнергияСкачать

Работа, совершаемая газом при расширении. Работа при изменении объёма газаСкачать

Физика. Термодинамика: Внутренняя энергия идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

Способы изменения внутренней энергииСкачать

Физика # 16. Внутренняя энергия, работа, расширение и теплоёмкость газаСкачать

Урок 170. Количество теплоты. Первый закон термодинамикиСкачать

Опыты по физике. Изменение внутренней энергии совершением механической работыСкачать

Газ просачивается из цилиндра, Внутренняя энергия, Задача 2 #МКТ #Физика #ЕГЭ #ОлимпиадыСкачать

Урок 111 (осн). Задачи на изменение внутренней энергииСкачать

Внутренняя энергия. Практическая часть. 10 класс.Скачать

Урок 105 (осн). Внутренняя энергия тела и способы ее изменения. Количество теплотыСкачать