2. Изображение пространственных фигур в параллельной проекции.
К изображению пространственных фигур в геометрии предъявляются требования:
1) верность; 2) наглядность; 3) простота выполнения.
Изображение считается верным, если оно передает одну из возможных проекций оригинала для выполнения этого требования достаточно при построении изображения использовать свойства параллельного проецирования и теоремы Польке – Шварца и Польке .С учетом 2 и 3 требования из возможных проекций оригинала выбирается та, которая наилучшим образом соответствует требованиям наглядности и содержит меньше дополнительных построений.
Опр. 1: Проекцией пространственной фигуры называется совокупность проекции всех ее точек.
Для получения проекции той или иной пространственной фигуры в общем случае не всегда нужно проецировать все ее точки. Например, для многогранника достаточно найти проекцию всех его вершин, а тогда будут определены проекции всех его ребер, граней, т. е. вся проекция многогранника. Далее будем считать, что плоскость проекции — плоскость чертежа, а проецируемая фигура расположена произвольно в пространстве и направлена параллельного проецирования произвольное. Поэтому можно говорить о произвольной параллельной проекции пространственных фигур.
Опр. 2: Канонической проекцией пространственной фигуры называется та проекция при которой изображение проекции наглядное и более простое.
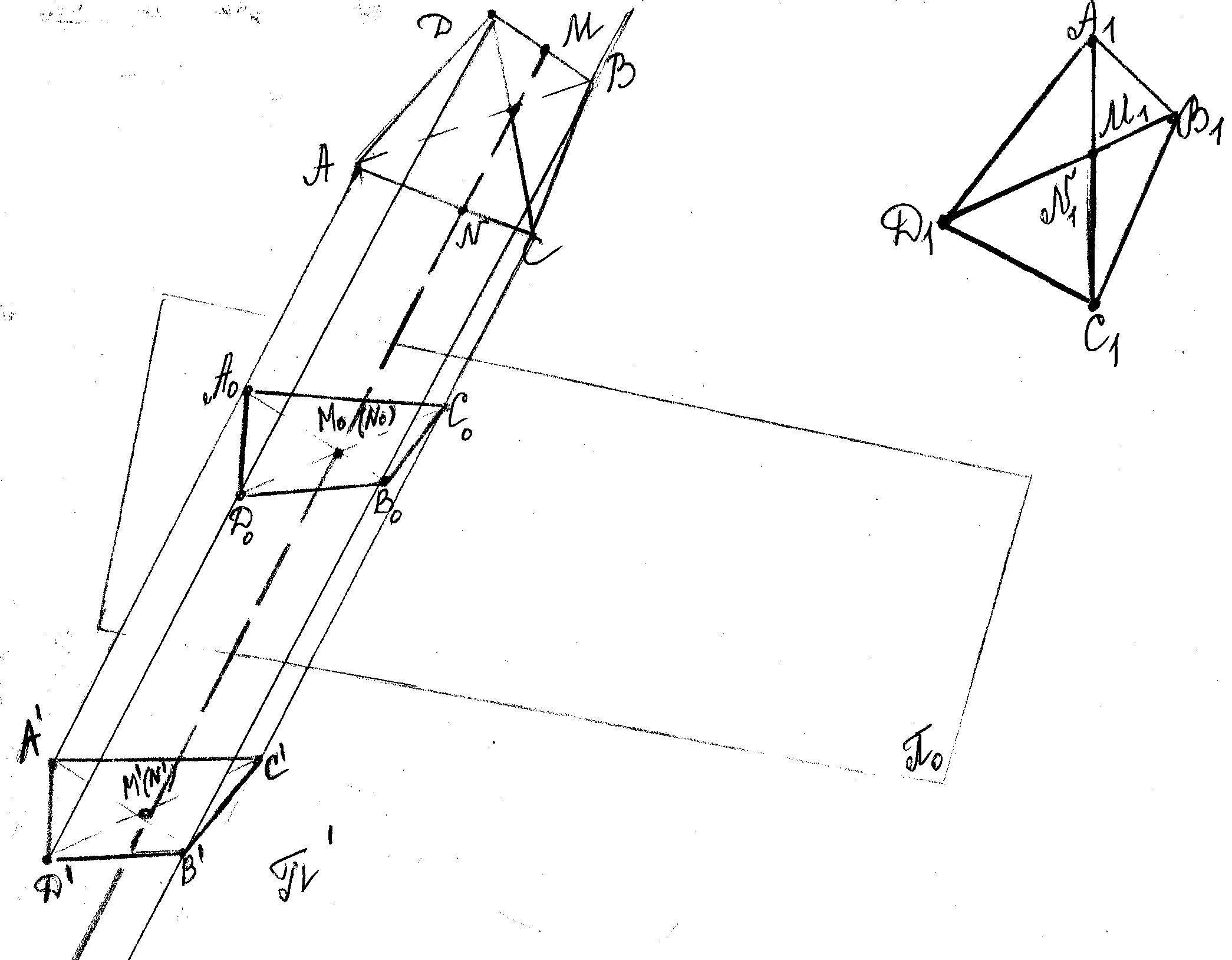
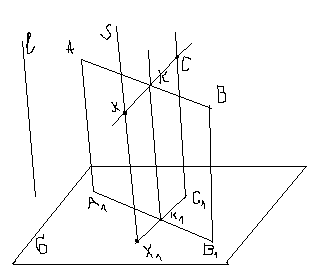
Теорема Польке – Шварца: Любой плоский 4-угольник A1B1C1D1 вместе с его диагоналями может
служить изображением тетраэдра ABCD произвольной формы.
Видео:Как нарисовать цилиндр, лежащий на горизонтальной плоскости. УрокСкачать
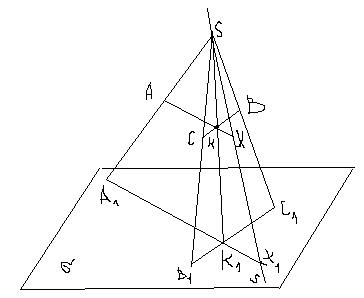
○ — диагонали, . Пусть ABCD произвольный тетраэдр. На ребре BD построим точку М: .На ребре АС построим точку М: . Примем прямую MN за направление проецирования. А плоскость проекций возьмем так, что MN . Найдем ортогональную проекцию тетраэдра на пл. , для этого найдем …..Получим 4-угольник A0B0C0D0 вместе с диагоналями, который является ортогональной проекцией тетраэдра на пл. . По свойствам параллельного проецирования имеем, что , но по условию (1). Аналогично, , но по условию , то (2). Получили, что для 4-уг. A1B1C1D1 и A0B0C0D0 выполняется условие теоремы*:Если два 4-угольника таковы, что их диагонали делятся в точке пересечения в отношениях одинаковых для обоих 4-угольников, то один из них (любой) является ортогональной проекцией некоторого 4-угольника подобного другому.
Чтобы принять следствие теоремы*: если основанием прямой призмы служит один из двух 4-угольников, удовлетворяющих теореме*, то среди плоских сечений такой призмы всегда можно указать такой 4-угольник, который будет подобен второму; продолжим прямые AA0, BB0, CC0, DD0 и примем их за ребра прямой призмы с основанием A0B0C0D0 и к этой призме применим следствие: Всякую прямую треугольную призму можно пересечь плоскостью так, что в сечении получиться треугольник любой наперед заданной формы. Среди плоских сечений этой призмы всегда найдется такой 4-угольник A ’ B ’ C ’ D ’ который будет подобен A1B1C1D1-данный 4-угольник.
Найденный 4-угольник A ’ B ’ C ’ D ’ с одной стороны подобен A1B1C1D1, с другой стороны является вместе с диагоналями параллельной проекцией тетраэдра на плоскость . Следовательно, данный 4-угольник A1B1C1D1 является изображением тетраэдра ABCD. Под изображением пространственной фигуры понимается либо ее проекция на плоскость проекции, либо фигура подобная ей.●
Читайте также: Блок цилиндров скания 124
Изображение призмы и пирамиды в параллельной проекции.
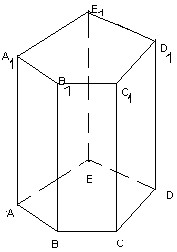
Построение изображения призм и пирамид в параллельной проекции, опирается на теорему Польке- Шварца и свойства параллельного проецирования. Построение этих тел начинается с построения изображения оснований.Пример: Построить прямую пятиугольную призму.
1 . Строим АВСДЕ.
2. т. к. призма прямая, то через вершину проводим прямые – боковые ребра, параллельные вертикальному обрезу листа (для наглядности).
Соединим вершины верхнего основания
Видео:Цилиндр, вытянутый вдоль оси Z. Урок33.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать
Изображение вершины пирамиды берется произвольно, но более наглядным изображением пирамиды считается такое, когда изображение высоты пирамиды параллельно боковому краю листа.
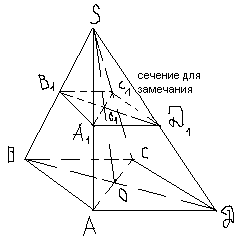
Пример: Построить правильную 4-угольную пирамиду SABCD.
, прямая s параллельна краю чертежа
Б ерем точку , S – вершина.
Замечание: При построении изображения усеченных пирамид нужно следить за тем, чтобы продолжения боковых ребер пересекались в одной точке- вершине полной пирамиды, то начинать надо с построения полной пирамиды.
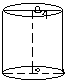
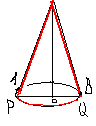
Изображение кругового цилиндра в параллельной проекции.
Нижнее основание цилиндра изображается в виде произвольного эллипса. Из центра этого эллипса откладывается в любом направлении отрезок произвольной длины, получим изображение центра верхнего основания цилиндра. Строим эллипс, равный начерченному, с центром в точке, полученной параллельным переносом из первого эллипса. Затем проводится общая касательная к этим эллипсам.
П ри изображении прямого кругового цилиндра основания (эллипсы) для наглядности проводят так, чтобы большая ось каждого из них была перпендикулярна боковому краю листа, а центры этих эллипсов лежали на общем перпендикуляре к большим осям. В этом случае крайние боковые образующие пройдут через концы большой оси каждого из эллипса.
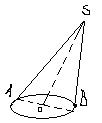
Изображение конуса вращения в параллельной проекции.
Видео:Как начертить цилиндр в объемеСкачать
О снование конуса изображается в виде произвольного эллипса независимо от формы конуса вращения. Проекцию S-его вершины можно выбрать произвольно, затем строится касательная из точки S к эллипсу.
М ожно установить, что точки касательной А и В конт. образующие SA и SB не являются диаметрально противоположными. Более наглядной проекцией конуса является такая, когда большая ось основания параллельна нижнему краю листа, а высота конуса перпендикулярна большой оси.
Замечание : При построении осевых сечений конуса, т. е. плоскостями, проходящими через ось нужно помнить, что крайняя образующая не является диаметрально противоположной.
Изображение шара в ортогональной проекции.
Обычно изображение шара строят только в ортогональной проекции, т. к. в этом случае проекция шара есть круг, а очерковая линия есть окружность, но это изображение являясь верным не является наглядным. Чтобы изображение шара стало наглядным, на чертеже строят проекции некоторых точек и линий, принадлежащих поверхности шара.Опр. 1: Полюсами шара называют точки пересечения поверхности шара с ее осью.Осью поверхности шара называют вертикальную прямую, проходящую через центр шара.Опр.2: Экватором шара называется линия пересечения поверхности шара с горизонтальной плоскостью, проходящей через центр шара.
Читайте также: Замена главного цилиндра сцепления ситроен джампер
Опр. 3: Параллелями шара называются линии пересечения поверхности шара с горизонтальными плоскостями, параллельными плоскости экватора.
Опр. 4: Меридианами шара называются линии пересечения поверхности шара с плоскостями, проходящими через ось шара.
Видео:Изображение фигур в параллельной проекции. Решение задач. Часть 2Скачать
До ортогонального проектирования шара мысленно отмечаем на поверхности шара экватор и полюс, затем наклоняем плоскость экватора или ось шара, чтобы она не была горизонтальной, но ось шара была параллельной профильной плоскости проекции, тогда экватор ортогонально проецируется в эллипс, отношение осей которого определяет наклон плоскости экватора к плоскости чертежа. Изображенный экватор, позволяет найти проекции полюсов. Для рисунка 1. С целью поиска проекции п олюсов, рассмотрим профильную плоскость, которая проходит через ось шара и перпендикулярна плоскости проекции, затем повернем ее вокруг линии пересечения этой плоскости с плоскостью чертежа до совмещения с плоскостью чертежа, тогда – профильная проекция экватораДля рисунка 2. Проводим , — профильная проекция оси шара. NS-фронтальная проекция оси шара. N-северный полюс, S – южный полюс.
Замечание: оказывается северный и южный полюса шара можно построить и не используя профильную проекцию. Рассмотрим треугольники ONN1 и D1DO они равны: ON1=D1O=R, как острые углы с соответственно перпендикулярными сторонами ON==DD1, NN1=OD.Поэтому, зная экватор шара можно построить полюсы без профильной проекции.Пусть: 1. AB, CD–оси экватора.2. строим DD1-касательная к экватору в т.D. DD1 параллельна AB. 3.строим N, S. ON=OS=DD1. Наоборот, если известны Nи S, то можно построить экватор без профильной проекции.
Построение:1. , 2.ON1, 3. , 4.проводим DD1 параллельно AB., 5.OC=OD,C NS. 6.AB и CD-оси экватора, по ним строим экватор.
О пр. 5: Точка называется заданной, если заданы проекция точки и проекция ее основания на основную плоскость. Опр. 6: Изображение называется полным, если все точки являются заданными (примеры полных изображений см. в лекциях). Опр.7:Задачи на построение на проекционном чертеже, в которой требуется определить общие элементы данных фигур, называются позиционными. Для решения позиционных задач достаточно, чтобы чертеж был полным. К позиционным задачам относятся все задачи на построение сечений многогранников, цилиндров, конусов. Эти сечения строят обычно двумя способами: 1. Способ следов. 2.Способ внутреннего проецирования.
С 
пособ следов. Под следом секущей пл. понимают прямую по которой пл. пересекается с какой-либо гранью многогранника, чаще всего с плоскостью нижнего основания многогранника или основной плоскостью. Этот способ основан на двух задачах: Построить точку пересечения (след), заданной прямой, с основной пл. .Прямая АВ задана, значит известна ее проекция на плоскость (А1В1). Ясно, что Х=АВ А1В1.Частный случай: Если АВ// , то решения (следа) нет.
Читайте также: Масло через прокладку блока цилиндров
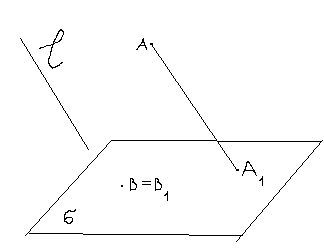
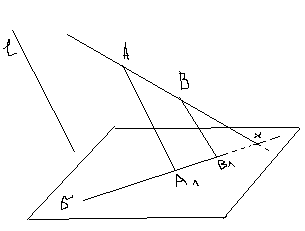
2. Секущая пл. определяется тремя заданными точками А(А1), В(В1), С(С1). Построить след этой плоскости в основной плоскости . Х=АВ А1В1. Х= ВС В1С1 ,р=(ХУ).
Способ внутреннего проецирования.Очень часто след секущей плоскости оказывается за пределами чертежа в этом случае проще использовать внутреннее проектирование.В случае призм и цилиндров применяют способ // внутреннего проектирования. Пирамиды, конусы — центральное внутреннее п роектирование (принимая за центр проецирования вершину пирамиды, конуса).
Этот способ основан на двух задачах:1. (для // внутреннего проектирования ). Секущая пл. задана А(А1), В(В1),С(С1). Дана пр. S-проецирующая соответствующая т. Х1. Построить т. Х=S . Построение: 1. К1=А1В1 С1Х1 2. К1 А1В1 К АВ, К1К//АА1 К=АВ К1К
Видео:Параллельная проекцияСкачать
3 .Х1 С1К1Х СК, Х SХ=S СК. 4. Х- искомая точка.
2. (для центрального внутреннего проецирования).
Даны S-центр внутреннего проецирования, центральные проекции А1, В1,С1 на основную пл. точек А, В, С секущей плоскости . S- произвольная проецирующая прямая: S=SX1, X1 . Построить точку Х пересечения пл. с прямой S.
точек А, В, С. о проецирования, центральные проекциинего проектирования. случае проще использовать внутреннее проектирование.
1. Отношение делимости в кольце целых чисел. Наибольший общий делитель и наименьшее общее кратное двух нат. чисел. Алгоритм Евклида. Критерий взаимной простоты двух нат. чисел.
Опр. Целое число а делит число b, если такое целое число сZ, такое что b=а·c (b-делимое, а-делитель, с-полное частное). (обозн. а|b).
Пример: 36|3, т.к. такое целое число 12, что 36 можно представить 36=3·12.
Отношение делимости рефлексивно: аZ а|а (любое целое число делится само на себя).
Отношение делимости транзитивно: целых а,в,сZ а|в и в|с а|с.
Отношение делимости сохраняется при изменении знака делимого и делителя.
Видео:Цилиндр, вытянутый вдоль оси X. Урок 35.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать
Если а|с и b|с, то сумма или разность тоже делится на с: а|с и в|с(ав)|с
Если а делится на с и b не делится на с, то сумма или разность не делится на с
9. Если а≠0, то не такого цел. числа q, что а=0·q, это значит, что а не равное нулю не делится на 0.
(НОД – общий делитель, кот. делится на любой общий делитель).
Пусть а, bN, b0. Осуществим деление с остатком по следующей схеме (делитель делим на остаток).
🎬 Видео
Цилиндр, вытянутый вдоль оси Y. Урок 34.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать
Параллельная ПроекцияСкачать
Вырез на цилиндре. Недостающие проекции выреза на теле вращения. Три проекции цилиндра с вырезом.Скачать
Проекции точек на поверхности цилиндра. Урок 36.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать
Параллельное проектирование и его свойства Изображение пространственных фигурСкачать
тема 8 3 Параллельное проектирование и его свойстваСкачать
Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать
Изометрическая проекция цилиндра. Чертим вместе.Скачать
Построение изометрии цилиндраСкачать
Проектирование.Изображение фигур в пространстве.Часть 1.Скачать
Параллельное проектирование и его свойстваСкачать
Цилиндр. Рассечение плоскостями. Урок 38.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать
Виды и изометрия цилиндраСкачать
Как нарисовать цилиндр.Полный разбор.Скачать
