Изобразить куб тетраэдр цилиндр параллелепипед конус пирамида (8 видео)

Содержание

Геометрические объекты: пирамида, призма, цилиндр, конус и другие
Рисунок «врезки»
Многогранники: призма, параллелепипед, куб
Конспект урока по математике на тему «Представление о плоских и объёмных фигурах. Геометрические тела: шар, пирамида, цилиндр, конус, куб, параллелепипед.»
🎥 Видео

Видео:Тема 71. Геометрические тела: шар, куб, пирамида, призма, цилиндр, конусСкачать

Геометрические объекты: пирамида, призма, цилиндр, конус и другие

3.2.3. геометрические объекты:

пирамида, призма, цилиндр, конус и другие

Пирамида – это многогранник, одна грань
которого многоугольник, а остальные грани –треугольники с общей вершиной (рисунок 3.54). Пирамида называется правильной, если в основании лежит правильный многоугольник и высота пирамиды проходит через центр многоугольника. Пирамида называется усеченной, если вершина ее отсекается плоскостью.

Многогранником называется геометрический объект, ограниченный совокупностью плоских многоугольников, у которых каждая сторона одного является одновременно стороной другого (но только одного).

Построение графического отображения многогранника сводится к построению проекций его вершин и ребер. Кратко охарактеризуем геометрические свойства некоторых многогранников и выполним их проекции.

Призма – многоугольник, две грани которого (основания призмы) представляют собой равные многоугольники с взаимно параллельными сторонами, а все другие грани – параллелограммы (рисунок 3.55). Название призмы зависит от того, какой многоугольник лежит в ее основании: если треугольник, то призма – треугольная, если четырехугольник, то – четырехугольная и т. д. Если основанием призмы является параллелограмм, то такая призма – параллелепипед. Призма называется прямой, если ее ребра перпендикулярны плоскости основания. Прямоугольный параллелепипед, все ребра которого конгруэнтны между собой, называется кубом.

Призматоид – многогранник, ограниченный двумя многоугольниками, расположенными в параллельных плоскостях (они являются его основаниями); его боковые грани представляют собой
треугольники и трапеции, вершины которых служат вершинами и многоугольников оснований (рисунок 3.56).

Многогранник, все грани которого представляют собой правильные и равные многоугольники, называют правильными. Углы при вершинах такого многогранника равны между собой. Существует пять типов правильных многогранников, свойства которых описал более двух тысяч лет назад древнегреческий философ Платон, чем и объясняется их общее название. Каждому правильному многограннику соответствует другой правильный многогранник с числом граней, равным числу вершин данного многогранника. Число ребер у обоих многогранников одинаково.

Тетраэдр – правильный четырехгранник. Он ограничен четырьмя равносторонними треугольниками. Это правильная треугольная пирамида.

Гексаэдр – правильный шестигранник. Это куб, ограниченный шестью равными квадратами.

Октаэдр – правильный восьмигранник, ограниченный восемью равносторонними и равными между собой треугольниками, соединенными по четыре у каждой вершины (рисунок 3.57).

Икосаэдр – правильный двадцатигранник, ограниченный двадцатью равносторонними и равными треугольниками, соединенными по пять у каждой вершины (рисунок 3.58).

Додекаэдр – правильный двенадцатигранник, ограниченный двенадцатью правильными и равными пятиугольниками, соединенными по три у каждой вершины (рисунок 3.59).

Кроме правильных выпуклых многогранников существуют и правильные выпукло-вогнутые многогранники. Их называют звездчатыми (самопересекающимися). Достраивая пересечения продолжений граней Платоновых тел, можно получать звездчатые многогранники. В качестве примера рассмотрим две наиболее простые звездчатые формы.

Звездчатый октаэдр. Восемь пересекающихся плоскостей граней октаэдра отделяют от пространства новые «куски», внешние по отношению к октаэдру. Это малые тетраэдры, основания которых совпадают с гранями октаэдра (рисунок 3.60). Его можно рассматривать как соединение двух пересекающихся тетраэдров, центры которых совпадают с центром исходного октаэдра. Такой звездчатый многоугольник в 1619 г. описал Кеплер и назвал его stella ostangula – восьмиугольная звезда.

Малый звездчатый додекаэдр – звездчатый додекаэдр первого продолжения. Он образован продолжением граней правильного выпуклого додекаэдра до их пересечения. Каждая грань выпуклого додекаэдра при продолжении сторон образует правильный звездчатый пятиугольник (рисунок 3.61). Пересекающиеся плоскости граней додекаэдра отделяют от пространства новые «куски», внешние по отношению к додекаэдру. Это двенадцать правильных пятиугольных пирамид, основания которых совпадают с гранями додекаэдра.

Читайте также: Блок цилиндров 501 мерседес

Цилиндр – геометрический объект, ограниченный цилиндрической поверхностью и двумя плоскостями, называемыми основаниями. В зависимости от угла наклона образующих цилиндрической поверхности к основанию различают прямой цилиндр (угол наклона 90°) и наклонный (рисунок 3.62).

Конус – геометрический объект, ограниченный конической поверхностью и плоскостью, называемой основанием или двумя плоскостями (усеченный конус). Конус может быть прямым (рисунок 3.63) или наклонным.

Шар – геометрический объект, образованный вращением круга вокруг его диаметра (рисунок 3.64). При сжатии или растяжении шар преобразуется в эллипсоид, который может быть получен вращением эллипса вокруг одной из осей: если вращение происходит вокруг большой оси, то эллипсоид называется вытянутым; если вокруг малой – сжатым, или сфероидом (рисунок 3.65).

Тор – геометрический объект, образованный при вращении круга вокруг оси, не проходящей через его центр (рисунок 3.66).

Видео:4 класс. Математика. Геометрические тела: шар, куб, пирамида, призма, цилиндр, конусСкачать

Рисунок «врезки»

«Врезкой» сокращенно называют задание по учебному перспективному рисунку, которое часто предлагают на вступительных экзаменах в художественные и архитектурные вузы.

«Врезка» — это абстрактная композиция из объемных геометрических тел, которые пересекаются между собой в пространстве, частично как бы вставлены, «врезаны» друг в друга. Геометрических фигур в такой композиции может быть довольно много, в среднем 5-10. Группа тел должна представлять некую цельную, достаточно эстетичную конструкцию, быть гармоничной, выразительной, и должна быть грамотно расположена в пространстве листа. Как правило, в задании предусмотрен формат А2.

Композицию нужно изобразить строго по правилам перспективы, с учетом точки зрения и положения линии горизонта.

Для компоновки врезки предлагается использовать основные, простейшие геометрические фигуры: куб, параллелепипед, шар, цилиндр, конус, призму, пирамиду. Фигуры можно делить на части, делать в них вырезы, но они должны оставаться узнаваемыми.

Предварительно, конечно, вы должны получить опыт рисования с натуры гипсовых геометрических тел.

Как правило, не рекомендуется ориентировать фигуры в пространстве под наклонными углами.

Самое сложное в этом задании — необходимость представить и правильно изобразить видимые и даже невидимые линии пересечения изображаемых объемных тел.

Мой совет — не стоит активно использовать такие взаимные пересечения тел, которые трудно себе представить мысленно, сложные по построению даже в виде чертежа. Не только прорисовать их пересечение сложно, но и оценить качество выполнения работы будет трудновато. Это, например, некоторые варианты взаимного пересечение цилиндра и шара, вообще тел вращения между собой. Более выразительны и понятны пересечения криволинейных поверхностей и плоскостей.

Пересечение шара и плоскости — всегда окружность, поэтому линия пересечения фигур пойдёт по эллипсу.

Видео:Миникурс по геометрии. Куб, призма, цилиндр и конусСкачать

Многогранники: призма, параллелепипед, куб

Определение

Многогранником будем называть замкнутую поверхность, составленную из многоугольников и ограничивающую некоторую часть пространства.

Отрезки, являющиеся сторонами этих многоугольников, называются ребрами многогранника, а сами многоугольники – гранями. Вершины многоугольников называются вершинами многогранника.

Будем рассматривать только выпуклые многогранники (это такой многогранник, который находится по одну сторону от каждой плоскости, содержащей его грань).

Многоугольники, из которых составлен многогранник, образуют его поверхность. Часть пространства, которую ограничивает данный многогранник, называется его внутренностью.

Определение: призма

Рассмотрим два равных многоугольника \(A_1A_2A_3. A_n\) и \(B_1B_2B_3. B_n\) , находящихся в параллельных плоскостях так, что отрезки \(A_1B_1, \ A_2B_2, . A_nB_n\) параллельны. Многогранник, образованный многоугольниками \(A_1A_2A_3. A_n\) и \(B_1B_2B_3. B_n\) , а также параллелограммами \(A_1B_1B_2A_2, \ A_2B_2B_3A_3, . \) , называется ( \(n\) -угольной) призмой.

Многоугольники \(A_1A_2A_3. A_n\) и \(B_1B_2B_3. B_n\) называются основаниями призмы, параллелограммы \(A_1B_1B_2A_2, \ A_2B_2B_3A_3, . \) – боковыми гранями, отрезки \(A_1B_1, \ A_2B_2, \ . A_nB_n\) – боковыми ребрами.
Таким образом, боковые ребра призмы параллельны и равны между собой.

Читайте также: Снятие главного тормозного цилиндра форд фокус 1

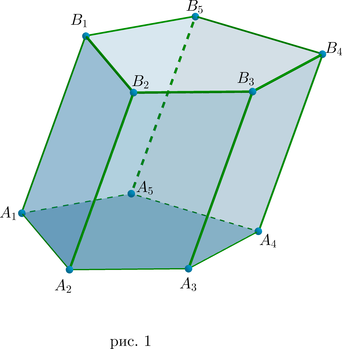
Рассмотрим пример — призма \(A_1A_2A_3A_4A_5B_1B_2B_3B_4B_5\) , в основании которой лежит выпуклый пятиугольник.

Высота призмы – это перпендикуляр, опущенный из любой точки одного основания к плоскости другого основания.

Если боковые ребра не перпендикулярны основанию, то такая призма называется наклонной (рис. 1), в противном случае – прямой. У прямой призмы боковые ребра являются высотами, а боковые грани – равными прямоугольниками.

Если в основании прямой призмы лежит правильный многоугольник, то призма называется правильной.

Определение: понятие объема

Единица измерения объема – единичный куб (куб размерами \(1\times1\times1\) ед \(^3\) , где ед — некоторая единица измерения).

Можно сказать, что объем многогранника – это величина пространства, которую ограничивает этот многогранник. Иначе: это величина, числовое значение которой показывает, сколько раз единичный куб и его части вмещаются в данный многогранник.

Объем имеет те же свойства, что и площадь:

1. Объемы равных фигур равны.

2. Если многогранник составлен из нескольких непересекающихся многогранников, то его объем равен сумме объемов этих многогранников.

3. Объем – величина неотрицательная.

4. Объем измеряется в см \(^3\) (кубические сантиметры), м \(^3\) (кубические метры) и т.д.

1. Площадь боковой поверхности призмы равна произведению периметра основания на высоту призмы.
Площадь боковой поверхности — сумма площадей боковых граней призмы.

2. Объем призмы равен произведению площади основания на высоту призмы: \[V_ >=S_ >\cdot h\]

Определение: параллелепипед

Параллелепипед – это призма, в основании которой лежит параллелограмм.

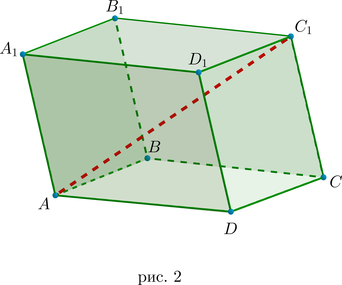
Все грани параллелепипеда (их \(6\) : \(4\) боковые грани и \(2\) основания) представляют собой параллелограммы, причем противоположные грани (параллельные друг другу) представляют собой равные параллелограммы (рис. 2).

Диагональ параллелепипеда – это отрезок, соединяющий две вершины параллелепипеда, не лежащие в одной грани (их \(8\) : \(AC_1, \ A_1C, \ BD_1, \ B_1D\) и т.д.).

Прямоугольный параллелепипед — это прямой параллелепипед, в основании которого лежит прямоугольник.
Т.к. это прямой параллелепипед, то боковые грани представляют собой прямоугольники. Значит, вообще все грани прямоугольного параллелепипеда – прямоугольники.

Все диагонали прямоугольного параллелепипеда равны (это следует из равенства треугольников \(\triangle ACC_1=\triangle AA_1C=\triangle BDD_1=\triangle BB_1D\) и т.д.).

Таким образом, параллелепипед обладает всеми свойствами призмы.

Площадь боковой поверхности прямоугольного параллелепипеда равна \[S_ >=2(a+b)c\]

Площадь полной поверхности прямоугольного параллелепипеда равна \[S_ >=2(ab+ac+bc)\]

Объем прямоугольного параллелепипеда равен произведению трех его ребер, выходящих из одной вершины (три измерения прямоугольного параллелепипеда): \[V_ >=abc\]

Доказательство

Т.к. у прямоугольного параллелепипеда боковые ребра перпендикулярны основанию, то они являются и его высотами, то есть \(h=AA_1=c\) Т.к. в основании лежит прямоугольник, то \(S_ >=AB\cdot AD=ab\) . Отсюда и следует данная формула.

Диагональ \(d\) прямоугольного параллелепипеда ищется по формуле (где \(a,b,c\) — измерения параллелепипеда) \[d^2=a^2+b^2+c^2\]

Доказательство

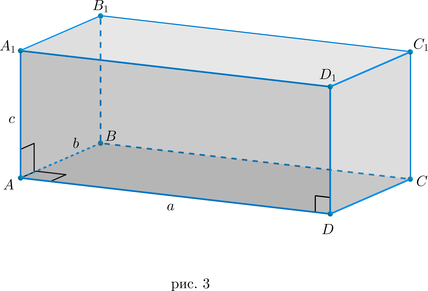
Рассмотрим рис. 3. Т.к. в основании лежит прямоугольник, то \(\triangle ABD\) – прямоугольный, следовательно, по теореме Пифагора \(BD^2=AB^2+AD^2=a^2+b^2\) .

Т.к. все боковые ребра перпендикулярны основаниям, то \(BB_1\perp (ABC) \Rightarrow BB_1\) перпендикулярно любой прямой в этой плоскости, т.е. \(BB_1\perp BD\) . Значит, \(\triangle BB_1D\) – прямоугольный. Тогда по теореме Пифагора \(B_1D=BB_1^2+BD^2=a^2+b^2+c^2\) , чтд.

Определение: куб

Куб — это прямоугольный параллелепипед, все грани которого – равные квадраты.

Таким образом, три измерения равны между собой: \(a=b=c\) . Значит, верны следующие

1. Объем куба с ребром \(a\) равен \(V_ >=a^3\) .

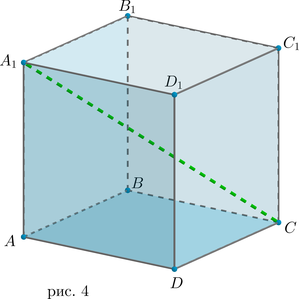
2. Диагональ куба ищется по формуле \(d=a\sqrt3\) .

3. Площадь полной поверхности куба \(S_ >=6a^2\) .

Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Конспект урока по математике на тему «Представление о плоских и объёмных фигурах. Геометрические тела: шар, пирамида, цилиндр, конус, куб, параллелепипед.»

Ищем педагогов в команду «Инфоурок»

УМК «Гармония». Математика. 2 класс.

Тема: Представление о плоских и объёмных фигурах. Геометрические тела: шар, пирамида, цилиндр, конус, куб, параллелепипед.

Читайте также: Не работает 4 цилиндр газель 4216 причины

Цель: Формировать представление о плоских и объёмных фигурах.

Познакомить учащихся с геометрическими телами (шар, пирамида, цилиндр, конус, куб, параллелепипед). Развивать воображение и пространственное мышление учащихся.

Догадайся, какие из данных фигур плоские? А какие объёмные?

Коллективное обсуждение. Диалог Миши и Маши даёт представление о возможных ответах второклассников на поставленный вопрос. Если ученики затрудняются, можно обратиться к диалогу Миши и Маши в учебнике.

а) . По какому признаку геометрические фигуры разложили на две группы?

Задание № 294. Учащиеся работают самостоятельно, в парах выбирая признак для каждой группы геометрических фигур (в верхнем ряду – плоские, в нижнем – объёмные).

б). Какая фигура «лишняя2 в каждом ряду?

В задании 295 дети самостоятельно выполняют классификацию, обосновывая свои действия в последующем обсуждении (в первом ряду «лишней» будет плоская геометрическая фигура шестиугольник, а во втором – объёмная геометрическая фигура цилиндр).

Работа по учебнику. Знакомство с правилом с. 96.

Геометрические фигуры (плоские или объёмные) являются идеальными объектами, которым нет аналогов в реальном мире вокруг нас. Именно поэтому при соотнесении данных объёмных тел с предметами окружающей действительности следует описывать каждый из них так: «По форме похож на…» или «Напоминает по форме…» и т. д.

Запись на доске слово «цилиндр»

– Знаете ли вы, что такое цилиндр? Назовите предметы, форма которых напоминает цилиндр.

Выслушав ответы (цистерна, стакан, ваза и т. д.).

– В переводе с греческого цилиндр означает «валик» или «катаю, вращаю». Где же используются валики? (Инструмент для малярных работ, подушка-валик или диванный валик.)

На доске написано слово «конус», в переводе с греческого означает это слово (заострённый предмет).

Назовите предметы, по форме напоминающие конус (колпак для новогоднего костюма звездочёта или Буратино, рожок для мороженого и т. д.).

Аналогичная работа проводится с шаром (в переводе с греческого – «мяч»). Дети называют предметы схожей формы.

Шар внутри не пустой: внутри него точки пространства, он заполнен

ими, как песком. Похожими на шар будут арбуз, апельсин, снежок, то есть те, которые внутри чем-то заполнены. И конечно, мяч – теннисный, футбольный, волейбольный и т. д.

Прочитайте названия геометрических тел из задания 296. Советуем приготовить строительный конструктор и иллюстрации с изображением архитектурных шедевров, по форме напоминающих данные

геометрические тела. Куб (рис. 4) и пирамида (рис. 8, 10), как показывает практика, учащимся знакомы не понаслышке. Из кубов, как из строительных деталей, дети строили дома (или замки). Некоторые ребята видели египетские пирамиды и уверенно показывают их на иллюстрациях.

Новыми словами (неизвестными для многих ребят) являются параллелепипед» и «призма».

Призма —— Параллелепипед —— Куб

На каком рисунке задания 296 изображён куб? (На рисунке 4.)

Один из ребят выходит к доске и подписывает номер рисунка под соответствующим названием, в итоге получаем:

Призма —— Параллелепипед —— Куб

На каких рисунках изображён параллелепипед.

( Вполне возможно, найдутся дети, знакомые с этим словом, они и подпишут номера рисунков под нужным словом. Если же ребята не могут выполнить данное требование, учитель делает запись сам и демонстрирует модели параллелепипеда (обувная коробка, коробка из-под бытовой техники и т. д.).

Куб – это параллелепипед, у которого все рёбра равны.

Запись на доске преобразуется:

Призма —— Параллелепипед —— Куб

В завершение работы записаны номера рисунков 4, 5, 6 и 7 (под словом «призма») и поясняет, что в геометрии призмой является и параллелепипед, и куб.