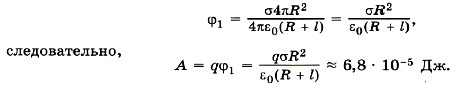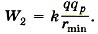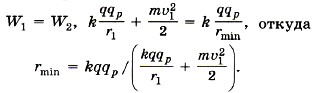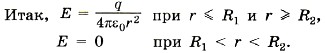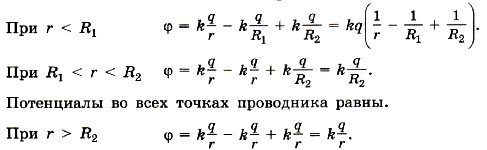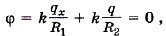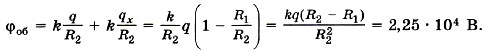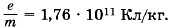Изобразите эквипотенциальные поверхности бесконечного проводящего равномерно заряженного цилиндра (7 видео)

Содержание

Решение упражнений к учебнику Г.Я.Мякишева, Б.Б.Буховцева
Эквипотенциальные поверхности. Эквипотенциальные линии их свойства.
§ 96. Примеры решения задач по теме «Потенциальная энергия электростатического поля. Разность потенциалов»
🎬 Видео

Видео:Физика. 10 класс. Эквипотенциальные поверхностиСкачать

Решение упражнений к учебнику Г.Я.Мякишева, Б.Б.Буховцева

1. В направленном вертикально вниз однородном электрическом поле напряженностью 1,3 • 10 5 В/м капелька жидкости массой 2 • 10 -9 г оказалась в равновесии. Определите заряд капельки и число избыточных электронов на ней.

2. Почему заряженная расческа притягивает электрически нейтральные кусочки бумаги?

3. Электрический заряд q1>0 переместили по замкнутому контуру ABCD в поле точечного заряда q2 > 0 (рис. 14.32). На каких участках работа поля по перемещению заряда была положительной? отрицательной? равной нулю? Как изменялась потенциальная энергия системы? Чему равна полная работа поля по перемещению заряда?

4. Двигаясь в электрическом поле, электрон перешел из одной точки в другую, потенциал которой выше на 1 В. Насколько изменилась кинетическая энергия электрона? потенциальная?

5. Точечные заряды q1 > 0 и q2

6. Потенциал электростатического поля возрастает в направлении снизу вверх. Куда направлен вектор напряженности поля?

7. Разность потенциалов между точками, лежащими на одной силовой линии на расстоянии 3 см друг от друга, равна 120 В. Определите напряженность электростатического поля, если известно, чти поле однородно.

8. Изобразите эквипотенциальные поверхности бесконечного проводящего и равномерно заряженного цилиндра.

9. У электрона, движущегося в электрическом поле, увеличилась скорость с v1=1• 10 7 м/с до v2 = 3 • 10 7 м/с. Определите разность потенциалов между начальной и конечной точками перемещения электрона. Отношение заряд f электрона к его массе равно: 1,76 • 10 11 Кл/кг.

Видео:Электрическое поле. Напряженность электрического поля. Силовые линии электрического поля. 10 класс.Скачать

Эквипотенциальные поверхности. Эквипотенциальные линии их свойства.

Эквипотенциальные поверхности это такие поверхности каждая из точек, которых обладают одинаковым потенциалом. То есть на эквипотенциальной поверхности электрический потенциал имеет неизменное значение. Такой поверхностью является поверхности проводников, так как их потенциал одинаков.

Представим себе такую поверхность, для двух точек которой разность потенциалов будет равна нулю. Это и будет эквипотенциальная поверхность. Поскольку потенциал на ней одинаков. Если рассматривать эквипотенциальную поверхность в двухмерном пространстве, допустим на чертеже, то она будет иметь форму лини. Работа сил электрического поля по перемещению электрического заряда вдоль этой лини будет равна нулю.

Одним из свойств эквипотенциальных поверхностей является то, что они всегда перпендикулярны силовым линиям поля. Это свойство можно сформулировать и наоборот. Любая поверхность, которая перпендикулярна во всех точках к линиям электрического поля и называется эквипотенциальной.

Также такие поверхности никогда не пересекаются между собой. Так как это означало бы различие потенциала в пределах одной поверхности, что противоречит определению. Еще они всегда замкнуты. Поверхности равного потенциала не могут начаться и уйти в бесконечность, не имея при этом четких границ.

Читайте также: Расположение цилиндров мерседес 276 мотор

Как правило, на чертежах нет необходимости изображать поверхности целиком. Чаще изображают перпендикулярное сечение к эквипотенциальным поверхностям. Таким образом, они вырождаются в линии. Этого оказывается вполне достаточно для оценки распределения данного поля. При изображении графически поверхности располагают с одинаковым интервалом. То есть между двумя соседними поверхностям соблюдается одинаковый, шаг скажем в один вольт. Тогда по густоте линий образованных сечением эквипотенциальных поверхностей можно судить о напряжённости электрического поля.

Для примера рассмотрим поле, создаваемое точечным электрическим зарядом. Силовые линии такого поля радиальные. То есть они начинаются в центре заряда и направлены на бесконечность, если заряд положительный. Или направлены к заряду, если он отрицательный. Эквипотенциальные поверхности такого поля будут иметь форму сфер с центром в заряде и расходящихся от него. Если же изобразить двухмерное сечение, то тогда эквипотенциальные лини будут в виде концентрических окружностей, центр которых также расположен в заряде.

Для однородного поля такого как, например поле между обкладками электрического конденсатора поверхности равного потенциала будут иметь форму плоскостей. Эти плоскости расположены параллельно друг другу на одинаковом расстоянии. Правда на краях обкладок картина поля исказится вследствие краевого эффекта. Но мы представим себе, что обкладки бесконечно длинные.

Чтобы изобразить эквипотенциальные лини для поля, создаваемого двумя равными по величине и противоположными по знаку зарядами не достаточно применить принцип суперпозиции. Так как в этом случае при наложении двух изображений точечных зарядов будут точки пересечения линий поля. А этого быть не может, так как поле не может быть направлено сразу в две разные стороны. В этом случае задачу необходимо решить аналитически.

Видео:Урок 231. Свойства электрического потенциалаСкачать

§ 96. Примеры решения задач по теме «Потенциальная энергия электростатического поля. Разность потенциалов»

При решении задач надо учитывать, что работа сил, действующих на заряд со стороны поля, выражается через разность потенциальных энергий или разность потенциалов (см. формулу (14.20)). Потенциал однородного поля определяется формулой (14.16), при этом надо всегда указывать, как выбран нулевой уровень потенциала.

Часто при решении задач надо учитывать, что все точки проводника в электростатическом поле имеют один и тот же потенциал, а напряжённость поля внутри проводника равна нулю.

Задача 1. Определите значение напряжённости и потенциала поля в точке А, находящейся на расстоянии l = 20 см от поверхности заряженной проводящей сферы радиусом R = 10 см, если потенциал сферы φ_₀ = 240 В.

Р е ш е н и е. Напряжённость поля сферы в точке А

где q₀ — заряд сферы. Потенциал сферы и потенциал поля в точке А равны соответственно

Читайте также: Рабочий цилиндр сцепления ваз 2105 ate

Выражая из формулы (2) заряд сферы q₀ и подставляя полученное выражение в формулы (1) и (3), получаем для напряжённости Ел и потенциала Фл следующие выражения:

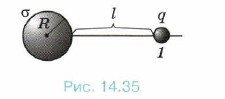
Задача 2. Какую работу А необходимо совершить, чтобы перенести заряд q = 3 • 10 -8 Кл из бесконечности в точку, находящуюся на расстоянии l = 90 см от поверхности сферы радиусом R = 10 см, если поверхностная плотность заряда сферы σ = 2 • 10 -6 Кл/м 2 ?

Р е ш е н и е. Работа, совершаемая при перенесении заряда q из бесконечности в точку 1 (рис. 14.35), равна увеличению потенциальной энергии заряда:

Так как площадь поверхности сферы равна 4πR 2 , то заряд сферы равен 4πR 2 σ. Тогда потенциал поля в точке 1

Задача 3. К закреплённому заряженному шарику зарядом +q движется протон. На расстоянии r = r₁ скорость протона υ₁. Определите, на какое минимальное расстояние приблизится протон к шарику.

Р е ш е н и е. Энергия протона на расстоянии r₁ равна сумме его потенциальной и кинетической энергий: 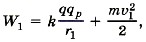на расстоянии r_min (протон останавливается) — только потенциальной энергии:

Кулоновская сила — консервативная, следовательно, можно записать закон сохранения энергии:

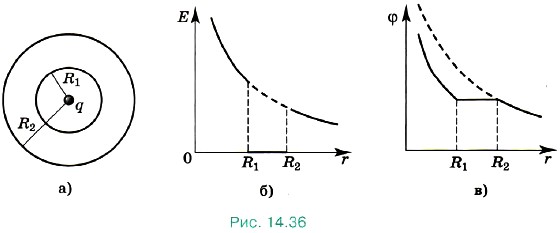
Задача 4. В центр незаряженной металлической сферической оболочки с внутренним радиусом R₁ и внешним радиусом R₂ помещают заряд q (рис. 14.36, а). Определите напряжённость и потенциал поля как функции расстояния от центра сферы.

Р е ш е н и е. Если заряд находится в центре, на внутренней поверхности металлической оболочки индуцируется заряд противоположного знака, а на внешней — того же знака, что и заряд q. При этом сумма индуцированных зарядов равна нулю (закон сохранения заряда).

Силовые линии поля начинаются на заряде q и заканчиваются на внутренней поверхности оболочки, а затем опять начинаются на внешней поверхности оболочки. Напряжённость электрического поля внутри проводника равна нулю. Картина силовых линий поля данной системы аналогична картине силовых линий поля точечного заряда за исключением области, занимаемой оболочкой. Здесь силовые линии терпят разрыв.

На рисунке 14.36, б изображена зависимость напряжённости Е(r).

Согласно принципу суперпозиции потенциал любой точки поля складывается из потенциала поля заряда q, проводящей сферы радиусом R₁, с зарядом -q и проводящей сферы радиусом R₂ с зарядом +q.

На рисунке 14.36, в изображена зависимость потенциала φ(r).

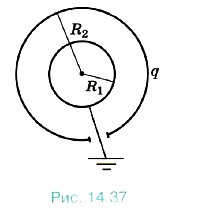
Задача 5. Металлический шарик радиусом R₁ = 20 см окружили тонкой сферической заряженной оболочкой, радиус которой R₂ = 40 см и заряд q = 2 • 10 -6 Кл (рис. 14.37). Определите потенциал оболочки и заряд шарика после того, как его заземлили.

Р е ш е н и е. После заземления шарика в системе будет происходить перетекание заряда до тех пор, пока потенциал шарика не станет равным нулю.

Читайте также: Главный тормозной цилиндр пассат б3 подключение

Потенциал шарика где q_x — заряд шарика. Отсюда q_x = -qR₁/R₂ = -10 -6 Кл.

Запишем выражение для потенциала оболочки и подставим в него выражение для заряда q_x шарика:

Задачи для самостоятельного решения

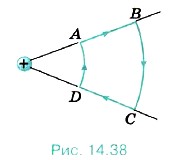
1. Электрический заряд q₁ > 0 переместили по замкнутому контуру ABCD в поле точечного заряда q₂ > 0 (рис. 14.38). На каких участках работа поля по перемещению заряда была положительной? отрицательной? равной нулю? Как изменялась потенциальная энергия системы? Чему равна полная работа поля по перемещению заряда?

2. Двигаясь в электрическом поле, электрон перешёл из одной точки в другую, потенциал которой выше на 1 В. Насколько изменилась кинетическая энергия электрона? потенциальная энергия электрона?

3. Два одинаковых шарика, имеющие одинаковые одноимённые заряды, соединены пружиной, жёсткость которой k = 10 3 Н/м, а длина l₀ = 4 см. Шарики колеблются так, что расстояние между ними изменяется от 3 до 6 см. Определите заряды шариков.

4. Разность потенциалов между точками, лежащими на одной силовой линии на расстоянии 3 см друг от друга, равна 120 В. Определите напряжённость электростатического поля, если известно, что поле однородно.

5. Изобразите эквипотенциальные поверхности бесконечного проводящего и равномерно заряженного цилиндра.

6. У электрона, движущегося в электрическом поле, увеличилась скорость с υ₁ ≈ 1 • 10 7 м/с до υ₂ ≈ 3 • 10 7 м/с. Определите разность потенциалов между начальной и конечной точками перемещения электрона. Отношение заряда электрона к его массе

7. Два небольших проводящих заряженных шара радиусом г расположены на расстоянии I друг от друга (l > 2г). Шары поочерёдно на некоторое время заземляют. Определите потенциал шара, который был заземлён первым. Первоначально каждый шар имел заряд q.

A1. Заряженная пылинка движется между двумя одинаковыми заряженными вертикальными пластинами, расположенными напротив друг друга. Разность потенциалов между пластинами 500 В, масса пылинки столь мала, что силой тяжести можно пренебречь. Какую кинетическую энергию приобретает пылинка при перемещении от одной пластины до другой, если её заряд 4 нКл?

1) 2 мкДж 2) 1 мкДж 3) 4 мкДж 4) 0,08 мкДж

A2. Заряженная пылинка движется вертикально между двумя одинаковыми горизонтальными пластинами размером 5X5 см, расположенными напротив друг друга на расстоянии 0,5 см, разность потенциалов между которыми 300 В. Её кинетическая энергия при перемещении от одной пластины до другой изменяется на 1,5 мкДж. Чему равен заряд пылинки? Силу тяжести не учитывайте.

1) 10 нКл 2) 1,5 нКл 3) 5 нКл 4) 0,25 нКл

C3. Песчинка, имеющая заряд 10 -11 Кл, влетела в однородное электрическое поле вдоль его силовых линий с начальной скоростью 0,1 м/с и переместилась на расстояние 4 см. Чему равна масса песчинки, если её скорость увеличилась на 0,2 м/с при напряжённости поля 10 5 В/м? Силу тяжести не учитывайте.