Изометрическая проекция усеченного цилиндра

Видео:Задание 38. Как начертить ИЗОМЕТРИЮ усеченного цилиндраСкачать

Развертка усеченного цилиндра. Построение развертки цилиндра.

Видео:усеченный цилиндр-ортогональные проекции-изометрия-разверткаСкачать

Развертка усеченного цилиндра. Построение развертки цилиндра.

Проекция цилиндра, срезанного плоскостью, наклонной к плоскости чертежа, по вертикальной плоскости проекции дает прямую линию, на горизонтальной — окружность, на профильной плоскости — замкнутую кривую, эллипс в искаженном виде.

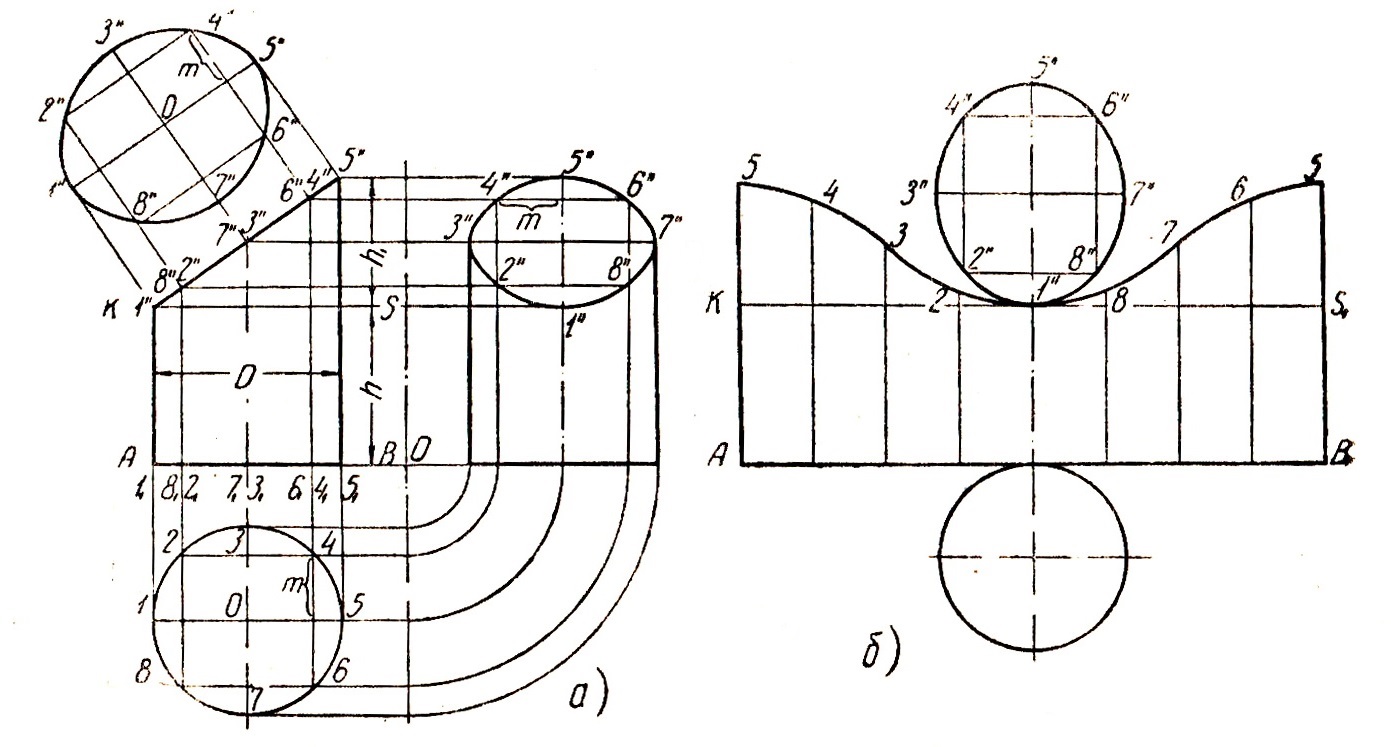
Если представить себе цилиндр, срезанный плоскостью KS (рис. 1, а), параллельной основанию и проходящей через низшую точку наклонного среза 1, то нижняя часть такого цилиндра развернется в прямоугольник A₁K₁S₁B₁ (рис. 1, б) с высотой h = BS и основанием А₁В₁ = πD.

Рис. 1. Развертка усеченного цилиндра:

а — проекция; б — развертка.

Развертка верхней части цилиндра.

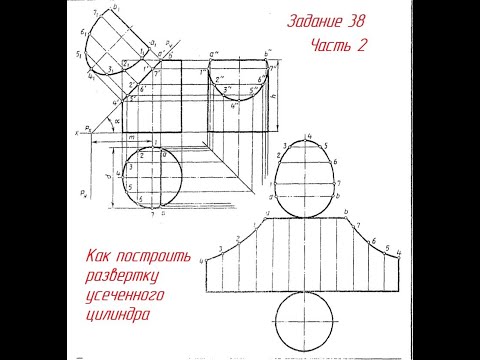
Чтобы получить развертку верхней части цилиндра выше плоскости KS, поступают следующим образом. Окружность основания делится на несколько равных частей, в приведенном примере на- восемь равных частей. Точки делений проектируют на вертикальную проекцию и проводят соответствующие образующие цилиндра 1₁ — 1′; 2₁ — 2″ и т. д. Затем делят длину развернутой окружности основания на такое же число равных частей, и из точек делений восстанавливают перпендикуляры, которые будут представлять собой те же образующие цилиндра, на которых затем нужно отложить их длины, измеряя одноименные отрезки на вертикальных проекциях (рис. 1, б). Соединив плавной кривой полученные точки, будем иметь развертку боковой поверхности усеченного цилиндра.

Для определения действительной формы поперечного сечения наклонной поверхности цилиндра вводят дополнительную плоскость проекции, параллельную плоскости сечения, на которой форма сечения спроектируется в искаженном виде — в форме эллипса.

Построение сечения цилиндра.

Для построения сечения на дополнительной плоскости проведем линию, параллельную проекции плоскости сечения, и, спроектировав на нее точки 1″ и 5″ с вертикальной проекции, получим большую ось эллипса. Затем из точки 7″ — 3″ на вертикальной проекции проведем линию, перпендикулярную большой оси эллипса, и, отложив на ней вправо и влево от большой оси отрезки 03″ и 07″, равные радиусу основания цилиндра, получим малую ось эллипса 3″ — 7″.

Положение остальных точек 2″, 4″, 6″, 8″ определяется так: на перпендикулярах к большей оси, проведенных из точек 8″ — 2″ и 6″ — 4″ вертикальной проекции, откладываем отрезки m от большей оси эллипса. Плавная кривая, проведенная через полученные восемь точек, будет эллипсом.

Построение эллипса на профильной проекции видно из рис. 1, а.

Для получения полной развертки поверхности цилиндра следует добавить поверхности наклонного сечения и нижнего основания цилиндра, как указано на рис. 1, б.

Видео:Усеченный цилиндр: проекции сечения, изометрия, развертка поверхностиСкачать

Урок 7. Сечение цилиндра плоскостью. Развертка усеченного цилиндра

Здравствуйте друзья! На этом уроке мы будем строить сечение цилиндра плоскостью и развертку усеченного цилиндра.

Читайте также: Двигатель 406 троит не работает 4 цилиндр

За основу возьмем модель цилиндра, построенного на втором уроке по 3d моделированию.

Видео:Задание 38. Как начертить РАЗВЕРТКУ УСЕЧЕННОГО ЦИЛИНДРАСкачать

Последовательность построения усеченного цилиндра

Пункты 1 — 4 аналогичны пунктам построения чертежа усеченной призмы .

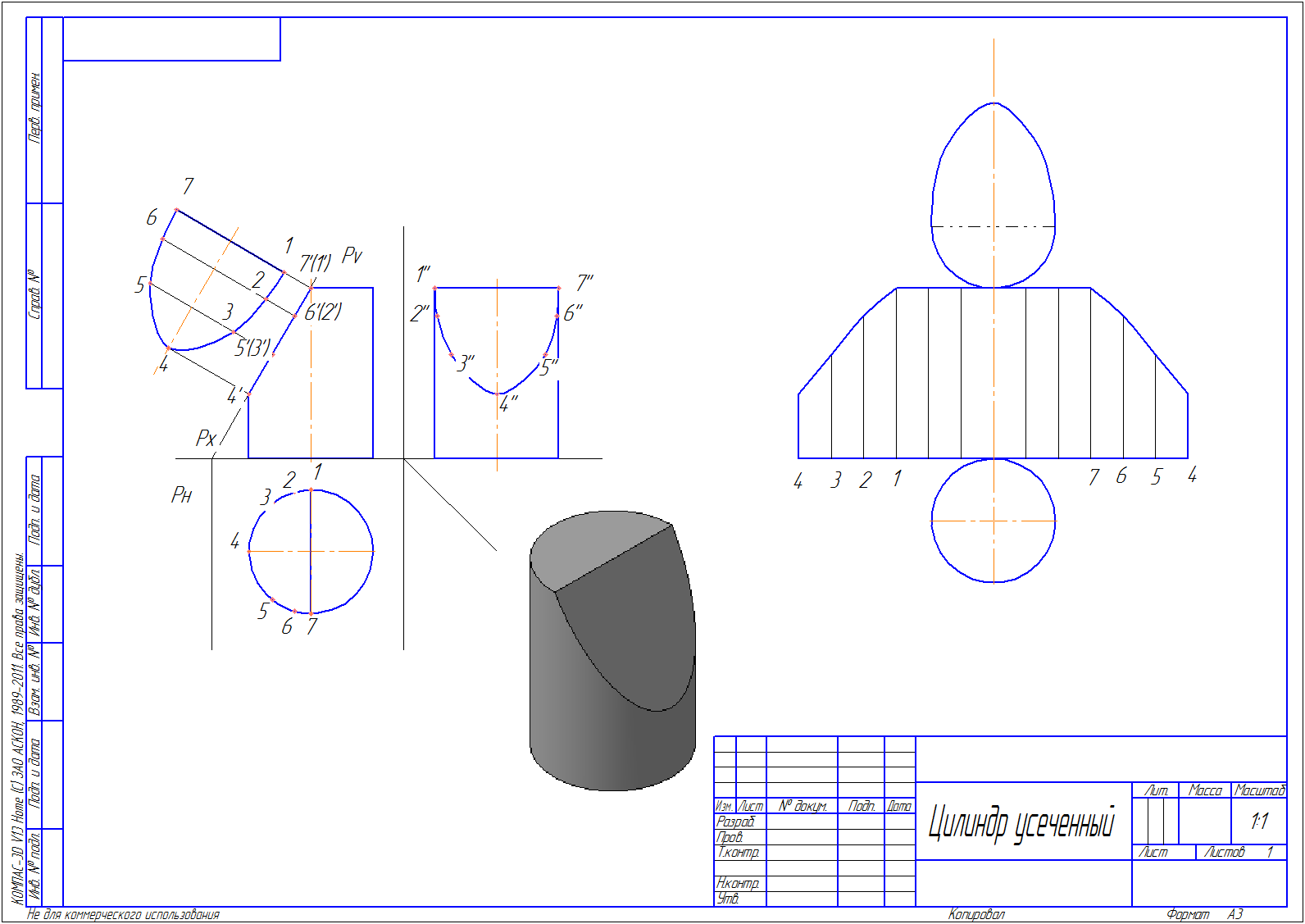
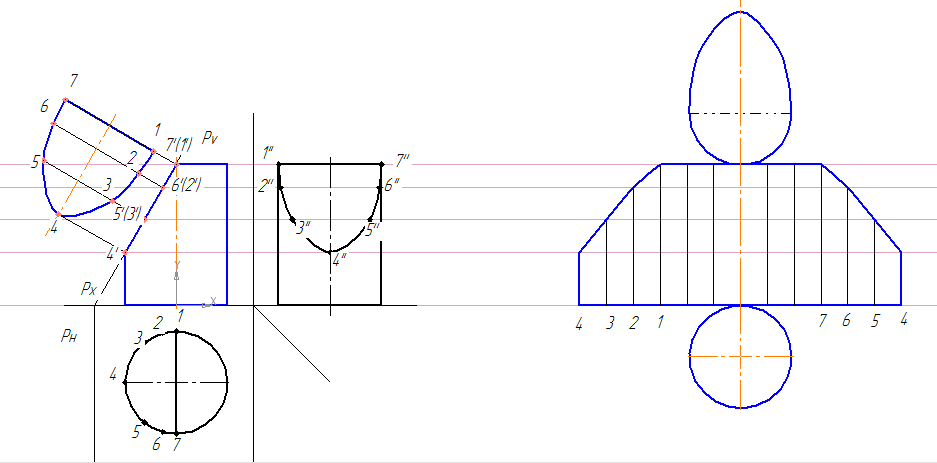
5. От оси симметрии цилиндра откладываем расстояние до следа секущей плоскости – 32 мм, проводим след секущей плоскости Pv под углом 60º.

6. Обозначаем несколько точек пересечения поверхности цилиндра со следом плоскости. Находим их на проекциях цилиндра. Соединяем точки при помощи кривой Безье. Получаем искаженные фигуры сечений.

7. Построим натуральный вид сечения

Построение натурального вида сечения цилиндра

8, 9 Построение аналогично построению сечения призмы

Развертка усеченного цилиндра

10. Развертку цилиндра будем строить на одной линии с осями x и y1.

11. Откладываем отрезок длиной l=π*D=3,14*40=125,6 мм.

12. Делим этот отрезок на 12 равных частей, нумеруем.

13. Переносим высоты отрезков с фронтальной проекции цилиндра. Соединяем полученные вершины при помощи кривой Безье. Натуральный вид сечения переносим копированием и поворотом. Достраиваем нижнее основание цилиндра.

Построение изометрии цилиндра

14. Наглядное изображение цилиндра сделаем при помощи рисунка. Для этого необходимо пересечение плоскостью цилиндра (3d модели).

15. Открываем деталь, в дереве модели выбираем плоскость xy. Строим эскиз, показанный на рисунке.

16. На компактной панели выбираем команду «Сечение по эскизу» . Задаем направление отсечения – прямое. Пересечение цилиндра плоскостью готово.

17. Сохраняем деталь в формате рисунка и вставляем его в чертеж. Оформляем чертеж.

Для лучшего понимания материала советую посмотреть небольшое видео по теме.

Как видите, построение сечения цилиндра плоскостью и развертки усеченного цилиндра, не такая уж и сложная задача вообще, а в Компасе построение идет гораздо проще.

Видео:Как начертить цилиндр в объемеСкачать

Изометрическая проекция (окончание)

Видео:Задание 38. Как построить УСЕЧЕННЫЙ ЦИЛИНДР. Построение НВ фигуры сечения. Часть 1Скачать

Изометрия окружности

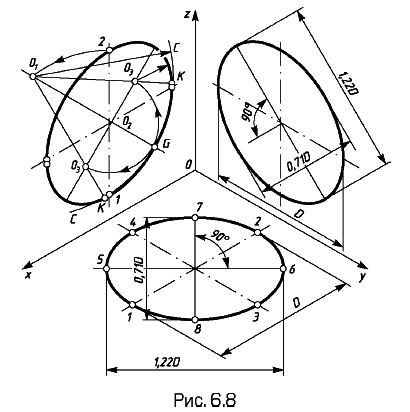
Окружности в изометрии изображаются в виде эллипсов (рис. 6.8) с указанием величин осей эллипсов для приведенных коэффициентов искажения, равных единице.

Большая ось эллипсов расположена под углом 90° для эллипсов, лежащих в плоскости xOz к оси у, в плоскости yOz к оси х, в плоскости xOy к оси z.

При построении изометрического изображения от руки (как рисунка) эллипс выполняют по восьми точкам. Например, по точкам 1, 2, 3, 4, 5, 6, 7 и 8 (см. рис. 6.8). Точки 1, 2, 3 и 4 находят на соответствующих аксонометрических осях, а точки 5, 6, 7 и 8 строят по величинам соответствующих большой и малой осей элипса. При вычерчивании эллипсы в изометрической проекции можно заменять овалами и строить их следующим образом 1 . Построение показано на рис. 6.8 на примере эллипса, лежащего в плоскости xOz. Из точки 1 как из центра, делают засечку радиусом R = D на продолжении малой оси эллипса в точке О₁ (строят также аналогичным образом и симметричную ей точку, которая на чертеже не показана). Из точки O₁ как из центра проводят дугу CGC радиуса D, которая является одной из дуг, составляющих контур эллипса. Из точки О₂ как из центра проводят дугу радиуса O₂G до пересечения с большой осью эллипса в точках О₃. Проводя через точки О₁, O₃ прямую, находят в пересечении с дугой CGCточку K, которая определяет O₃K — величину радиуса замыкающей дуги овала. Точки K являются также точками сопряжения дуг, составляющих овал.

Читайте также: Подбор тормозных цилиндров по размерам

Видео:Развертка усеченного цилиндраСкачать

Изометрия цилиндра

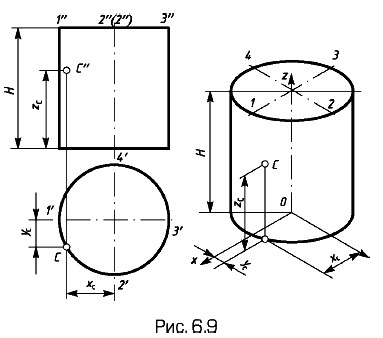
Изометрическое изображение цилиндра определяется изометрическими изображениями окружностей его основания. Построение в изометрии цилиндра высотой Н по ортогональному чертежу (рис. 6.9, слева) и точки С на его боковой поверхности показано на рис. 6.9, справа.

Пример построения в изометрической проекции круглого фланца с четырьмя цилиндрическими отверстиями и одним треугольным приведен на рис. 6.10. При построении осей цилиндрических отверстий, а также ребер треугольного отверстия использованы их координаты, например координаты х₀ и y₀.

Видео:Построение изометрии усеченного цилиндра │Урок #60Скачать

Изометрическая проекция усеченного цилиндра

Видео:Цилиндр, вытянутый вдоль оси Z. Урок33.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

§ 13. Построение аксонометрических проекций

Построение аксонометрических проекций начинают с проведения аксонометрических осей.

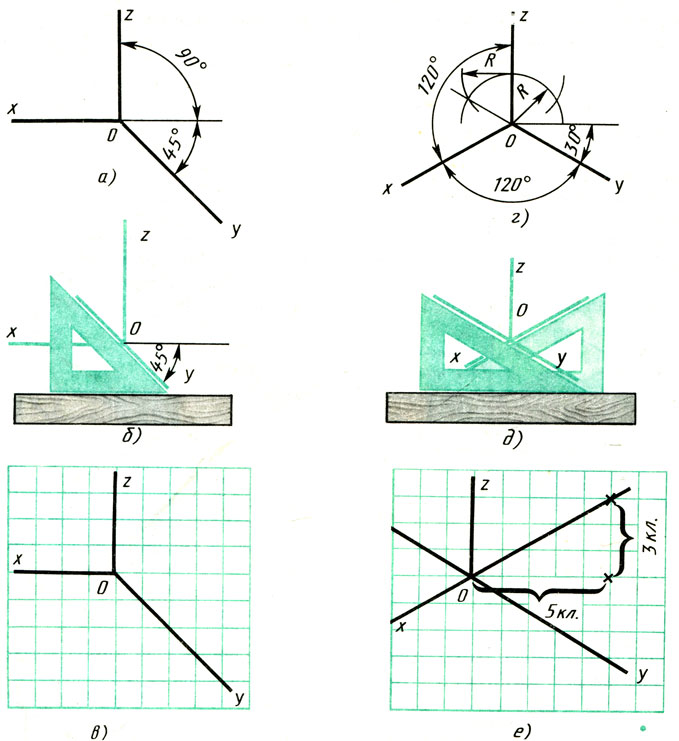
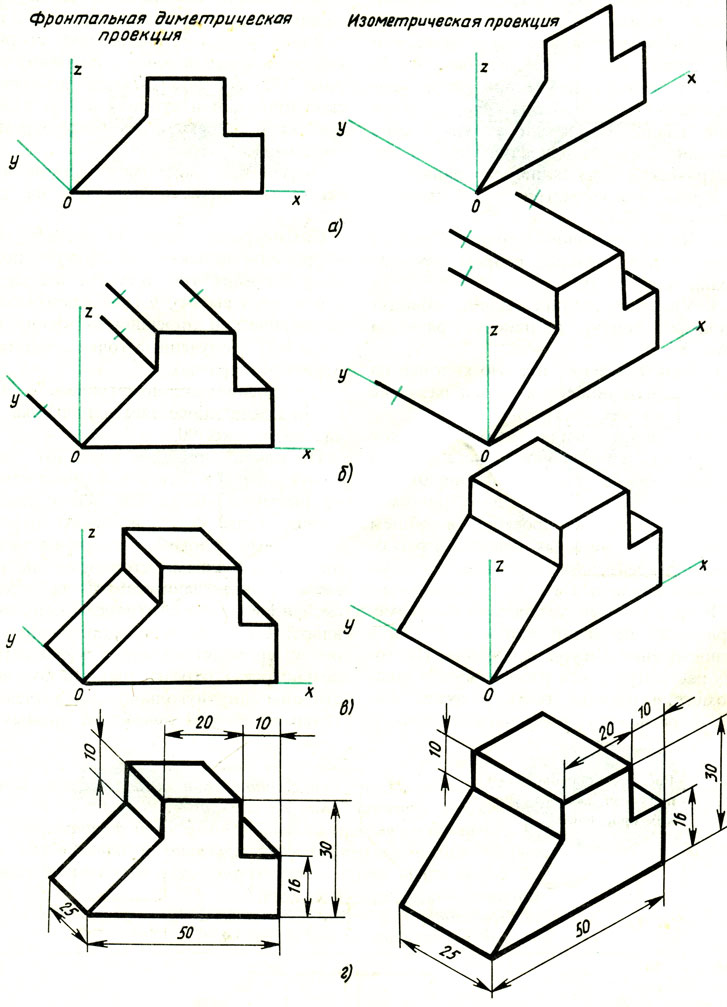
Положение осей. Оси фронтальной ди-метрической проекции располагают, как показано на рис. 85, а: ось х — горизонтально, ось z — вертикально, ось у — под углом 45° к горизонтальной линии.

Угол 45° можно построить при помощи чертежного угольника с углами 45, 45 и 90°, как показано на рис. 85, б.

Положение осей изометрической проекции показано на рис. 85, г. Оси х и у располагают под углом 30° к горизонтальной линии (угол 120° между осями). Построение осей удобно проводить при помощи угольника с углами 30, 60 и 90° (рис. 85, д).

Чтобы построить оси изометрической проекции с помощью циркуля, надо провести ось z, описать из точки О дугу произвольного радиуса; не меняя раствора циркуля, из точки пересечения дуги и оси z сделать засечки на дуге, соединить полученные точки с точкой О.

При построении фронтальной диметрической проекции по осям х и z (и параллельно им) откладывают действительные размеры; по оси у (и параллельно ей) размеры сокращают в 2 раза, отсюда и название «диметрия», что по-гречески означает «двойное измерение».

При построении изометрической проекции по осям х, у, z и параллельно им откладывают действительные размеры предмета, отсюда и название «изометрия», что по-гречески означает «равные измерения».

На рис. 85, в и е показано построение аксонометрических осей на бумаге, разлинованной в клетку. В этом случае, чтобы получить угол 45°, проводят диагонали в квадратных клетках (рис. 85, в). Наклон оси в 30° (рис. 85, г) получается при соотношении длин отрезков 3 : 5 (3 и 5 клеток).

Рис. 85. Способы построения осей аксонометрических проекций

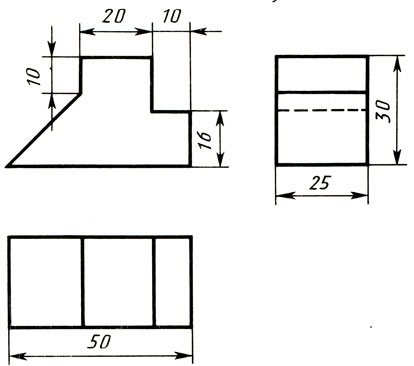
Построение фронтальной диметрической и изометрической проекций. Построить фронтальную диметрическую и изометрическую проекции детали, три вида которой приведены на рис. 86.

Рис. 86. Комплексный чертеж детали

Порядок построения проекций следующий (рис. 87):

1. Проводят оси. Строят переднюю грань детали, откладывая действительные величины высоты — вдоль оси z, длины — вдоль оси х (рис. 87, а).

2. Из вершин полученной фигуры параллельно оси v проводят ребра, уходящие вдаль. Вдоль них откладывают толщину детали: для фронтальной ди-метрической проекции — сокращенную в 2 раза; для изометрии — действительную (рис. 87, б).

Читайте также: В установке известны масса однородного сплошного цилиндра его радиус

3. Через полученные точки проводят прямые, параллельные ребрам передней грани (рис. 87, в).

4. Удаляют лишние линии, обводят видимый контур и наносят размеры (рис. 87, г).

Сравните левую и правую колонки на рис. 87. Что общего и в чем различие данных на них построений?

Рис. 87. Способ построения аксонометрических проекций

Из сопоставления этих рисунков и приведенного к ним текста можно сделать вывод о том, что порядок построения фронтальной диметрической и изометрической проекций в общем одинаков. Разница заключается в расположении осей и длине отрезков, откладываемых вдоль оси у.

В ряде случаев построение аксонометрических проекций удобнее начинать с построения фигуры основания. Поэтому рассмотрим, как изображают в аксонометрии плоские геометрические фигуры, расположенные горизонтально.

Построение аксонометрической проекции квадрата показано на рис. 88, а и б.

Вдоль оси х откладывают сторону квадрата а, вдоль оси у — половину стороны а/2 для фронтальной диметрической проекции и сторону а для изометрической проекции. Концы отрезков соединяют прямыми.

Рис. 88. Аксонометрические проекции квадрата: а — фронтальная диметрическая; б — изометрическая

Построение аксонометрической проекции треугольника показано на рис. 89, а и б.

Симметрично точке О (началу осей координат) по оси х откладывают половину стороны треугольника а/2, а по оси у — его высоту h (для фронтальной диметрической проекции половину высоты h/2). Полученные точки соединяют отрезками прямых.

Рис. 89. Аксонометрические проекции треугольника: а — фронтальная диметрическая; б — изометрическая

Построение аксонометрической проекции правильного шестиугольника показано на рис. 90.

По оси х вправо и влево от точки О откладывают отрезки, равные стороне шестиугольника. По оси у симметрично точке О откладывают отрезки s/2, равные половине расстояния между противоположными сторонами шестиугольника (для фронтальной диметрической проекции эти отрезки уменьшают вдвое). От точек m и n, полученных на оси у, проводят вправо и влево параллельно оси х отрезки, равные половине стороны шестиугольника. Полученные точки соединяют отрезками прямых.

Рис. 90. Аксонометрические проекции правильного шестиугольника: а — фронтальная диметрическая; б — изометрическая

Ответьте на вопросы

1. Как располагают оси фронтальной диметрической и изометрической проекций? Как их строят?

2. Какие размеры откладывают вдоль осей фронтальной диметрической и изометрической проекций и параллельно им?

3. Вдоль какой аксонометрической оси откладывают размер уходящих вдоль ребер предмета?

4. Назовите общие для фронтальной диметрической и изометрической проекций этапы построения.

Задания к § 13

Упражнение 40

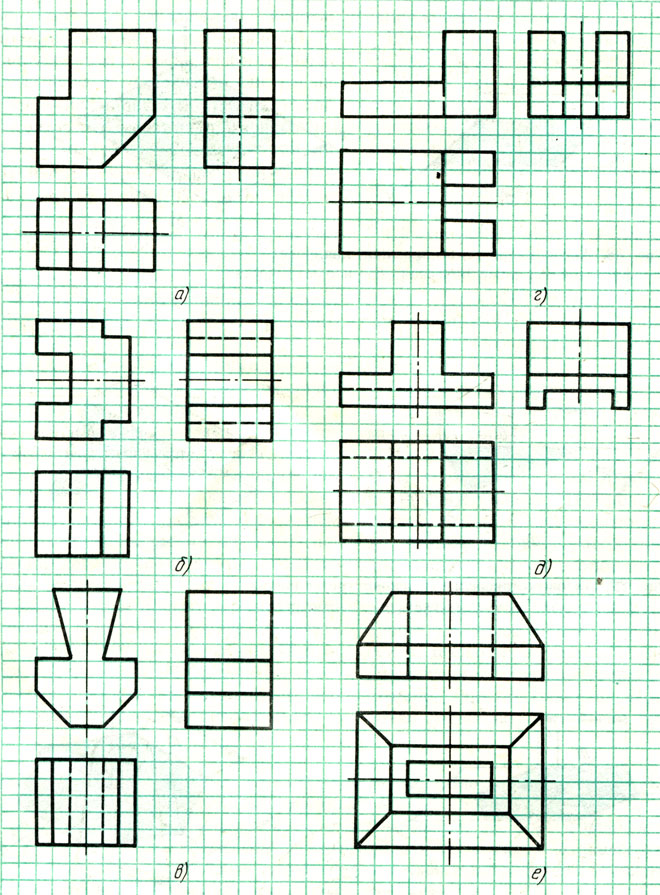
Постройте аксонометрические проекции деталей, приведенных на рис. 91, а, б, в — фронтальные диметрические, для деталей на рис. 91, г, д, е — изометрические.

Размеры определите по числу клеток, считая, что сторона клетки равна 5 мм.

В ответах дано по одному примеру последовательности выполнения заданий.

Рис. 91. За типе на построение аксонометрических проекций

Упражнение 41

Постройте в изометрической проекции правильные четырехугольную, треугольную и шестиугольную призмы. Основания призм расположены горизонтально, длина сторон основания 30 мм, высота 70 мм.

В ответах дан пример последовательности выполнения задания.

🔍 Видео

Построение изометрии цилиндраСкачать

Рисуем усеченный цилиндр.Скачать

Построение усеченного цилиндра с сечением в натуральную величинуСкачать

Цилиндр, вытянутый вдоль оси X. Урок 35.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Часть 1 Усечённый цилиндрСкачать

Как построить ЛИНИЮ ПЕРЕСЕЧЕНИЯ двух ЦИЛИНДРОВСкачать

Как начертить КОНУС С ВЫРЕЗОМ (чертеж + аксонометрия)Скачать

Изометрическая проекция цилиндра. Чертим вместе.Скачать

Часть 1. Изометрическая проекция. (стр. 29)Скачать

Усеченный конус: проекции сечения, изометрия и развертка поверхностиСкачать