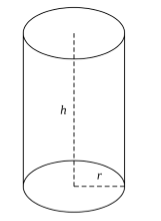
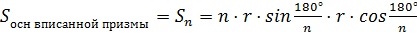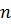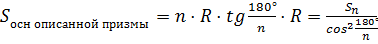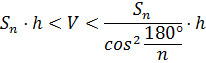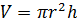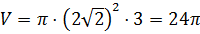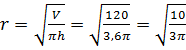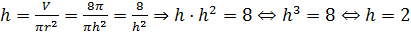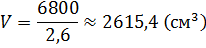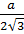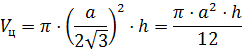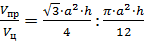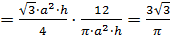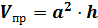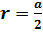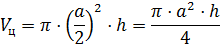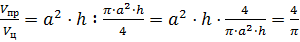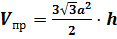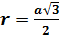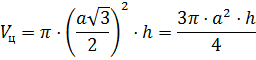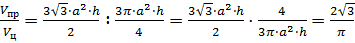Тела вращения – это объемные тела, которые возникают при вращении некой плоской фигуры, которая ограничена кривой и крутится вокруг оси, лежащей в той же плоскости. К телам вращения относятся цилиндр, конус и шар.
Цилиндр — это объемное тело, которое получается при вращении прямоугольника вокруг одной из его сторон.
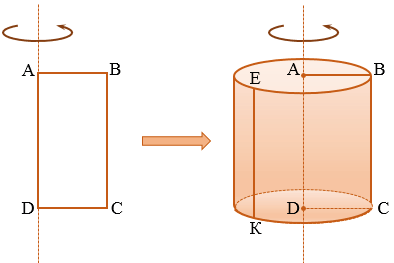
Возьмем прямоугольник АВСD. Будем вращать этот прямоугольник против часовой стрелки вокруг стороны АD.
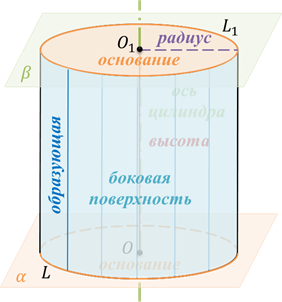
Прямая АD — ось цилиндра.
Отрезок АD — высота цилиндра.
Основания цилиндра — два равных круга образованных при вращении сторон АВ и DC (круги равные, т.к. стороны АВ и DC равны как противоположные стороны прямоугольника).
Радиус цилиндра — радиус оснований цилиндра.
Цилиндрическая поверхность (или боковая поверхность цилиндра) — поверхность, образованная при вращении стороны ВС и состоящая из отрезков, параллельных оси цилиндра (АD).
Образующие цилиндра — отрезки, из которых составлена боковая поверхность цилиндра (на рисунке выше указаны образующие ВС и ЕК).
- Определение
- Объем цилиндра
- Доказательство:
- Площадь боковой поверхности цилиндра
- Цилиндр
- Понятие цилиндра
- Виды цилиндров
- Площадь поверхности цилиндра
- Готовые работы на аналогичную тему
- Объем цилиндра
- Пример задачи
- Что такое цилиндр: определение, элементы, виды, варианты сечения
- Определение цилиндра
- Основные элементы цилиндра
- Объем цилиндра
- Урок 24. Геометрия 11 класс ФГОС
- В данный момент вы не можете посмотреть или раздать видеоурок ученикам
- Получите невероятные возможности
- Конспект урока «Объем цилиндра»
- 💡 Видео
Определение
Объем цилиндра
Доказательство:
Дано: цилиндр с площадью основания S, высотой h и объемом V.
Доказать: V = Sh.
Доказательство:
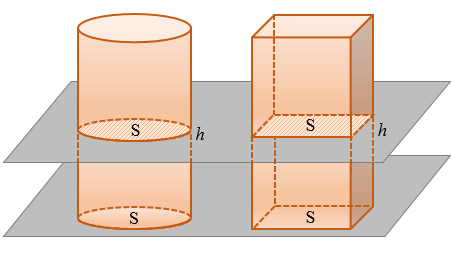
Воспользуемся принципом Кавальери. Рассмотрим цилиндр и призму с площадями оснований, равными S, и высотами, равными h, «стоящие» на одной плоскости.
Любая секущая плоскость, параллельная плоскости, на которой стоят цилиндр и призма, дает в качестве сечения цилиндра круг площади S, а в качестве сечения призмы — многоугольник площади S. Значит, объем цилиндра равен объему призмы. Но объем призмы равен Sh. Поэтому и объем цилиндра равен Sh, т.е. V = Sh. Что и требовалось доказать.
Площадь боковой поверхности цилиндра
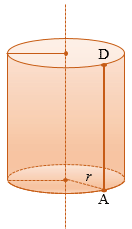
Рассмотрим цилиндр с радиусом r и высотой h.
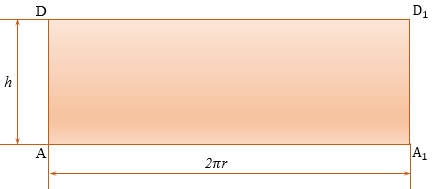
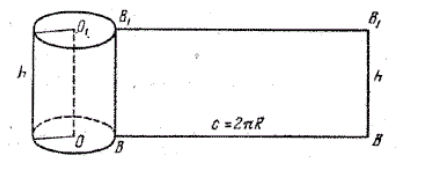
Представим, что его боковую поверхность разрезали по одной из его образующих АD и развернули так, что получился прямоугольник АDА1D1, стороны АD и А1D1 которого являются двумя краями разреза боковой поверхности цилиндра. Этот прямоугольник называется разверткой боковой поверхности цилиндра.
Сторона АА1 прямоугольника АDА1D1 равна длине окружности основания, а сторона АD равна высоте цилиндра, т.е. АА1 = 2 r, АВ = h. Площадь прямоугольника равна произведению его смежных сторон, значит, площадь прямоугольника АDА1D1 равна 2 rh.
Площадь Sбок боковой поверхности цилиндра равна площади ее развертки, т.е. Sбок = 2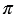 rh. rh. |
Поделись с друзьями в социальных сетях:
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Цилиндр
Вы будете перенаправлены на Автор24
Видео:Видеоурок по математике "Цилиндр"Скачать

Понятие цилиндра
Геометрическая фигура, образованная двумя равными кругами, лежащими в параллельных плоскостях, все точки которых соединены между параллельными прямыми, так что никакая точка не остается несоединенной, называется цилиндром (рис. 1).
Читайте также: Как поменять главный цилиндр сцепления ман тга
Круги при этом называются основаниями цилиндра, а прямые их соединяющие — образующими. Прямая, которая проходит через центры окружностей оснований называется осью цилиндра, а совокупность всех образующих — боковой поверхностью цилиндра.
Видео:Объём цилиндраСкачать

Виды цилиндров
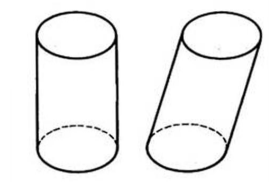
Цилиндр, у которого все образующие перпендикулярны к плоскостям, проходящим через основания, называется прямым. В противном же случае он является наклонным (рис. 2).
Рисунок 2. Прямой и наклонный цилиндры
Видео:Нумерация цилиндров, как определить где какой номер цилиндра?/how to determine cylinder number?Скачать

Площадь поверхности цилиндра
Площадь поверхности цилиндра определяется следующим образом:
Найдем теперь формулы для вычисления площадь боковой поверхности и основания.
Так как в основании лежат круги, то очевидно, что
Площадь боковой поверхности цилиндра определяется как произведение длины окружности, ограничивающей основание цилиндра на его высоту.
Доказательство.
Для доказательства этой теоремы нам необходимо найти площадь развертки боковой поверхности цилиндра (рис. 3).
Видим, что разверткой боковой поверхности цилиндра является прямоугольник. Высота прямоугольника равняется высоте цилиндра $h$, а длина равняется длине окружности, ограничивающей основание цилиндра, то есть
Готовые работы на аналогичную тему
Теорема доказана.
Видео:КАК ИЗМЕРИТЬ ЦИЛИНДРЫ? Учимся пользоваться нутромером и микрометромСкачать

Объем цилиндра
Объем цилиндра определяется как произведение площади основания цилиндра на его высоту.
Доказательство.
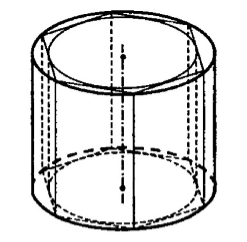
Рассмотрим цилиндр с радиусом $r$ и высотой $h$. Найдем ее объем $V$. Для этого сначала впишем в нее правильную $n-$угольную призму, в которую впишем еще один цилиндр. Пусть радиус второго цилиндра равняется $r’$, а её объем равен $V’$ (рис. 4).
Как мы знаем, объем призмы будет равен $S_ h$. Следовательно, получим следующую оценку
Теорема доказана.
Видео:Как доказать ДПС по номеру двигателя что у тебя Альфа 50 кубов а не 110Скачать

Пример задачи
Найти площадь полной поверхности цилиндра и его объем, если радиус его основания равняется $7$ см, а высота в два раза больше диаметра основания.
Найдем вначале высоту цилиндра. Так как высота в два раза больше диаметра, получим
\[V=\pi r^2h=49\pi \cdot 28=1372\pi \]
Ответ: $490\pi ,\ 1372\pi $
Видео:как замерить выработку поршня и цилиндраСкачать

Что такое цилиндр: определение, элементы, виды, варианты сечения
В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения одной из самых распространенных трехмерных геометрических фигур – цилиндра. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.
Видео:не растачивайте цилиндры пока не посмотрите это видео!Скачать

Определение цилиндра
Далее мы подробно остановимся на прямом круговом цилиндре как самой популярной разновидности фигуры. Другие ее виды будут перечислены в последнем разделе данной публикации.
Прямой круговой цилиндр – это геометрическая фигура в пространстве, полученная путем вращения прямоугольника вокруг своей стороны или оси симметрии. Поэтому такой цилиндр иногда называют цилиндром вращения.
Цилиндр на рисунке выше получен в результате вращения прямоугольного треугольника ABCD вокруг оси O1O2 на 180° или прямоугольников ABO2O1/O1O2CD вокруг стороны O1O2 на 360°.
Видео:Микрометр и нутромер. Как измерить цилиндры?Скачать

Основные элементы цилиндра
- Основания цилиндра – два одинаковых по размеру/площади круга с центрами в точках O1 и O2.
- R – радиус оснований цилиндра, отрезки AD и BC – диаметры (d).
- O1O2 – ось симметрии цилиндра, одновременно является его высотой (h).
- l (AB, CD) – образующие цилиндра и одновременно с этим стороны прямоугольника ABCD. Равны высоте фигуры.
Читайте также: Компрессия в цилиндрах двигателя норма логан
Развёртка цилиндра – боковая (цилиндрическая) поверхность фигуры, развернутая в плоскость; является прямоугольником.
- длина данного прямоугольника равна длине окружности основания цилиндра ( 2πR );
- ширина равна высоте/образующей цилиндра.
Примечание: формулы для нахождения площади поверхности и объема цилиндра представлены в отдельных публикациях.
Видео:Как доказать ДПС, что у тебя 50 кубов, а не 110. Мопед Альфа RX 11Скачать

Объем цилиндра
Урок 24. Геометрия 11 класс ФГОС
Видео:Как использовать кросс-цилиндрСкачать

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Объем цилиндра»
На этом уроке мы вспомним определение цилиндра, основные элементы цилиндра, выведем формулу для вычисления объёма цилиндра.
Тело, ограниченное цилиндрической поверхностью и двумя равными кругами с границами 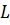
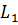
Можно ещё услышать и такое определение:
Прямым круговым цилиндром или просто цилиндром называется геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями 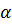
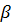
Назовём элементы цилиндра.
Круги называются основаниями цилиндра.
Отрезки образующих, заключенные между основаниями, — образующими цилиндра.
А образованная ими часть цилиндрической поверхности это есть боковая поверхность цилиндра.
Ось цилиндрической поверхности называется осью цилиндра.
Как уже отмечалось ранее, все образующие цилиндра параллельны и равны друг другу. Длина образующей называется высотой цилиндра, а радиус основания – радиусом цилиндра.
Цилиндр называется равносторонним, если его высота равна диаметру основания.
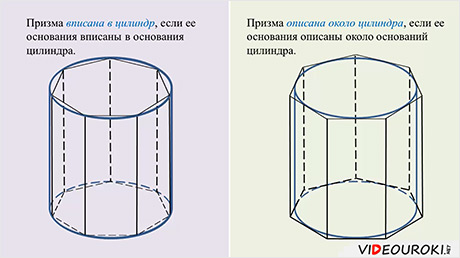
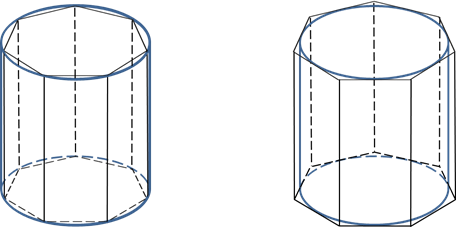
Говорят, что призма вписана в цилиндр, если её основания вписаны в основания цилиндра, и призма описана около цилиндра, если её основания описаны около оснований цилиндра.
Нетрудно увидеть, что высота любой призмы, вписанной в цилиндр или описанной около него, равна высоте самого цилиндра.
Теперь давайте сформулируем и докажем теорему о вычислении объёма цилиндра.
Объём цилиндра равен произведению площади основания на высоту.
Доказательство. Пусть нам дан цилиндр, радиус которого равен 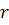
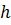
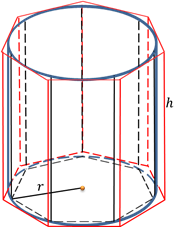
Впишем в этот цилиндр правильную -угольную призму. Поскольку призма правильная, значит, в основании этой призмы лежит правильный -угольник.
Давайте вернёмся в планиметрию и вспомним формулу для нахождения площади правильного многоугольника вписанного около окружности. Поскольку этот многоугольник является основанием прямой призмы, значит, площадь основания призмы будет вычисляться по формуле .
Теперь давайте вокруг этого же цилиндра опишем -угольную призму с таким же количеством сторон.
Вернёмся в планиметрию и вспомним формулу для нахождения площади правильного многоугольника описанного около окружности. Поскольку этот многоугольник является основанием прямой призмы, значит, площадь основания призмы будет вычисляться по формуле .
Так как эта призма содержится в цилиндре, а цилиндр содержится в этой призме, то, значит, объём цилиндра больше объёма одной призмы и меньше объёма второй призмы.
Читайте также: Блок цилиндров газель 406 двигатель
Объём прямой призмы вычисляется по формуле произведение площади основания призмы на высоту призмы.
Если увеличивать количество сторон основания призмы, то площадь основания призм будет стремиться к площади круга, тогда объём этих призм будет стремиться к 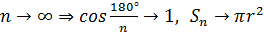
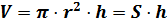
Что и требовалось доказать.
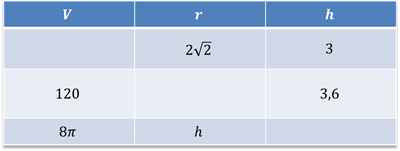
Задача: заполнить таблицу недостающими данными.
Решение: в первой строке нам известны радиус основания цилиндра и высота цилиндра, для того, чтобы найти объём цилиндра, воспользуемся только что доказанной формулой .
Занесём получившееся значение в ячейку.
Во второй строке нам даны объем цилиндра и его высота, для того чтобы найти радиус основания цилиндра, выразим из формулы объёма радиус . Занесём получившееся значение в ячейку.
В третьей строке нам даны: объём цилиндра и его радиус, который равен высоте цилиндра. Подставим эти значения в известную нам формулу и получим .
Задача: алюминиевый провод 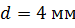
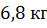
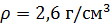
Решение: для решения этой задачи, нам нужны будут знания из физики. Мы знаем, что для вычисления массы используется формула: 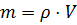
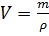
Не забудем перевести килограммы в граммы.
Провод представляет собой цилиндр.
Длина провода будет высотой этого цилиндра. То есть наша задача сводится к нахождению высоты цилиндра.
Диаметр провода равен 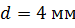
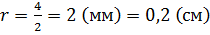
Из формулы для вычисления объёма цилиндра выразим высоту 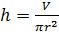
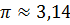
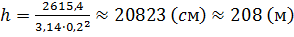
Задача: в цилиндр вписана правильная -угольная призма. Найти отношение объёмов призмы и цилиндра, если призма треугольная, четырёхугольная, шестиугольная.
Решение: применим известные нам формулы для вычисления объёмов правильной призмы 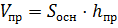
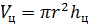
Сегодня на уроке мы говорили, что если призма вписана в цилиндр, то её высота равна высоте цилиндра 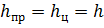
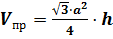
Радиус цилиндра будет равен .
Тогда отношение объёмов правильной призмы и цилиндра будет равно
.
Если в цилиндр вписана четырёхугольная призма, то объём призмы равен
.
Радиус цилиндра будет равен .
Тогда отношение объёмов призмы и цилиндра равно .
Если в цилиндр вписана шестиугольная призма, то объём призмы равен .
Радиус цилиндра будет равен .
Тогда отношение объёмов призмы и цилиндра равно .
Сегодня на уроке мы вспомнили какая фигура называется цилиндром, повторили основные элементы цилиндра, вывели формулу для вычисления объёма цилиндра, рассмотрели несколько задач на применение этой формулы.
💡 Видео
11 класс, 32 урок, Объем цилиндраСкачать

ЗАДИРОВ в цилиндрах НЕ БУДЕТ если делать так...Скачать

Хон или зеркало? Научно-практический коментарийСкачать

Сперматозоид-чемпион | наглядно показано оплодотворениеСкачать

Что такое хонингование цилиндров двигателя? Особенности, как делается и для чего нужно?Скачать

КАК РЕШАТЬ ЗАДАЧИ ПО ГЕОМЕТРИИ? | МатематикаСкачать

Зачем на стенках цилиндров нового двигателя наносят царапины. Хонингование, что этоСкачать

Устройство саморазводящегося рабочего тормозного цилиндра.Скачать

Задача, которую боятсяСкачать