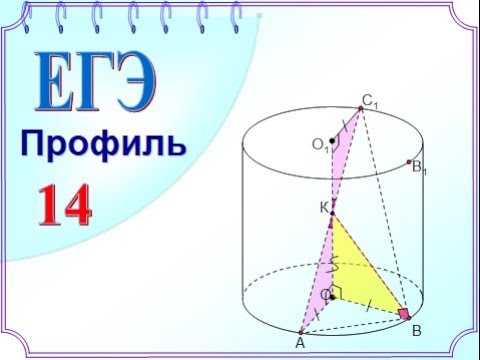
Задание 14. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А, В и С, а на окружности другого основания — точка C1, причём СС1 — образующая цилиндра, а АС — диаметр основания. Известно, что угол ACB = 30°, АВ = √2 , СС1 = 4.
а) Докажите, что угол между прямыми АС1 и ВС равен 60°.
б) Найдите площадь боковой поверхности цилиндра.
а) Треугольник ABC – прямоугольный, так как AC – диаметр. Проведем прямую AP параллельную BC. В результате угол между AC1 и BC будет таким же, что и угол между AC1 и AP.
Отрезок CC1 – образующая цилиндра, которая перпендикулярна плоскости ABC, следовательно, (так как CP параллельна AB). Учитывая, что , по теореме о трех перпендикулярах следует, что треугольник C1PA – прямоугольный. Далее, рассмотрим прямоугольный треугольник C1CP с C1C=4, CP=√2 (так как CP=BA), получаем:
Рассмотрим треугольник ABC, в котором угол ACB равен 30° и, зная AB=√2, получаем AC=2√2. Далее,
Рассмотрим треугольник C1PA, в котором
б) Площадь боковой поверхности цилиндра . Рассмотрим прямоугольный треугольник ABC с гипотенузой AC, т.к. AC – диаметр. Учитывая, что AB=√2, AC=2√2, имеем: . Высота h=CC1=4 и
Видео:✓ Задача про цилиндр | ЕГЭ-2018. Задание 14. Математика. Профильный уровень | Борис ТрушинСкачать
Как доказать что угол прямой в цилиндре
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В1 и С1, причем ВВ1 — образующая цилиндра, а отрезок АС1 пересекает ось цилиндра.
а) Докажите, что угол АВС1 прямой.
б) Найдите площадь боковой поверхности цилиндра, если AB = 20, BB1 = 15, B1C1 = 21.
а) Рассмотрим плоскость, проходящую через ось цилиндра и прямую АС1. Обозначим точку пересечения этой плоскости и окружности основания цилиндра, содержащую точку А, через точку С. Тогда СС1 — образующая цилиндра. Отрезок АС пересекает ось цилиндра. Значит, он проходит через центр окружности основания цилиндра, то есть является ее диаметром. Следовательно, угол АВС прямой.
Читайте также: Замена манжетов главного тормозного цилиндра газ 31105
Прямая СС1 является образующей цилиндра, поэтому она перпендикулярна прямой АВ. Таким образом, прямая АВ перпендикулярна плоскости ВСС1б а значит, угол АВС1 прямой.
б) Отрезок AC является диаметром основания цилиндра. Значит, длина
окружности основания цилиндра равна
Следовательно, площадь боковой поверхности цилиндра равна
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,
Видео:2 задание ЕГЭ профиль стереометрияСкачать
Как доказать что угол прямой в цилиндре
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В1 и С1, причем ВВ1 — образующая цилиндра, а отрезок АС1 пересекает ось цилиндра.
а) Докажите, что угол АВС1 прямой.
а) Рассмотрим плоскость, проходящую через ось цилиндра и прямую АС1. Обозначим точку пересечения этой плоскости и окружности основания цилиндра, содержащую точку А, через точку С. Тогда СС1 — образующая цилиндра. Отрезок АС пересекает ось цилиндра. Значит, он проходит через центр окружности основания цилиндра, то есть является ее диаметром. Следовательно, угол АВС прямой.
Прямая СС1 является образующей цилиндра, поэтому она перпендикулярна прямой АВ. Таким образом, прямая АВ перпендикулярна двум пересекающимся прямым, лежащим в плоскости ВСС1 (BС и СС1), а значит, прямая АВ перпендикулярна плоскости ВСС1 и любой прямой, лежащей в этой плоскости, в том числе и ВС1. Значит, угол АВС1 прямой.
б) Поскольку прямые ВВ1 и СС1 параллельны, искомый угол равен углу АС1С.
Треугольники АВС и АСС1 являются прямоугольными, поэтому:
Приведем другой способ решений.
a) Введем систему координат, как показано на рисунке. Найдем координаты точек A, B и C1. Пусть а радиус основания — r, тогда
Найдем координаты векторов и
Найдем скалярное произведение векторов и
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,
Видео:Задача, которую боятсяСкачать
Как доказать что угол прямой в цилиндре
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В1 и С1, причем ВВ1 — образующая цилиндра, а отрезок АС1 пересекает ось цилиндра.
а) Докажите, что угол АВС1 прямой.
а) Рассмотрим плоскость, проходящую через ось цилиндра и прямую АС1. Обозначим точку пересечения этой плоскости и окружности основания цилиндра, содержащую точку А, через точку С. Тогда СС1 — образующая цилиндра. Отрезок АС пересекает ось цилиндра. Значит, он проходит через центр окружности основания цилиндра, то есть является ее диаметром. Следовательно, угол АВС прямой.
Прямая СС1 является образующей цилиндра, поэтому она перпендикулярна прямой АВ. Таким образом, прямая АВ перпендикулярна двум пересекающимся прямым, лежащим в плоскости ВСС1 (BС и СС1), а значит, прямая АВ перпендикулярна плоскости ВСС1 и любой прямой, лежащей в этой плоскости. Значит, угол АВС1 прямой.
б) Треугольник ABC1 прямоугольный, поэтому искомое расстояние равно его высоте h, проведённой к гипотенузе. Получаем:
Аналоги к заданию № 520803: 520853 520879 520915 Все
Видео:Геометрия 11 класс (Урок№12 - Объемы прямой призмы и цилиндра.)Скачать
Как доказать что угол прямой в цилиндре
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки А и В, а на окружности другого основания — точки В1 и С1, причем ВВ1 — образующая цилиндра, а отрезок АС1 пересекает ось цилиндра.
а) Докажите, что угол АВС1 прямой.
а) Рассмотрим плоскость, проходящую через ось цилиндра и прямую АС1. Обозначим точку пересечения этой плоскости и окружности основания цилиндра, содержащую точку А, через точку С. Тогда СС1 — образующая цилиндра. Отрезок АС пересекает ось цилиндра. Значит, он проходит через центр окружности основания цилиндра, то есть является ее диаметром. Следовательно, угол АВС прямой.
Прямая СС1 является образующей цилиндра, поэтому она перпендикулярна прямой АВ. Таким образом, прямая АВ перпендикулярна двум пересекающимся прямым, лежащим в плоскости ВСС1 (BС и СС1), а значит, прямая АВ перпендикулярна плоскости ВСС1 и любой прямой, лежащей в этой плоскости. Значит, угол АВС1 прямой.
б) Поскольку прямые ВВ1 и СС1 параллельны, искомый угол равен углу АС1С.
Треугольники АВС и АСС1 являются прямоугольными, поэтому:
Приведем другой способ решений.
a) Введем систему координат, как показано на рисунке. Найдем координаты точек A, B и C1. Пусть а радиус основания — r, тогда
Найдем координаты векторов и
Найдем длины векторов и
Найдем косинус угла между этими векторами:
Значит, угол АВС1 прямой.
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки,
Аналоги к заданию № 520803: 520853 520879 520915 Все
🎥 Видео
11 класс, 32 урок, Объем цилиндраСкачать
Сложная 2-я задача Профиля #егэ #математика #геометрия #стереометрия #цилиндр #шар #репетиторСкачать
Угол между прямой и плоскостью. Видеоурок по геометрии 10 классСкачать
Как решать задачи про площадь боковой поверхности цилиндра и конуса #математика #егэ #shortsСкачать
Центр кругаСкачать
11 класс. Геометрия. Объем цилиндраСкачать
Студенты российского вуза разработали вечный двигатель #вечныйдвигатель #изобретенияСкачать
Стереометрия 10 класс. Часть 1 | МатематикаСкачать
ЕГЭ Задание 14 Цилиндр Теорема о трёх перпендикулярахСкачать
ТРИ ПРИЗНАКА РАВЕНСТВА ТРЕУГОЛЬНИКОВ НА ЕГЭ #shorts #математика #егэ #огэ #профильныйегэ #геометрияСкачать
Регулировка развал - схождение с помощью IPhone 11 лайфхакер.Скачать
Точка, линия на поверхности прямого кругового цилиндра. Сечение плоскостью наклонного цилиндра.Скачать
Объемы прямой призмы и цилиндраСкачать
Найдите угол: задача по геометрииСкачать
SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать
Вагнеровцы после обороны Бахмута #shortsСкачать
