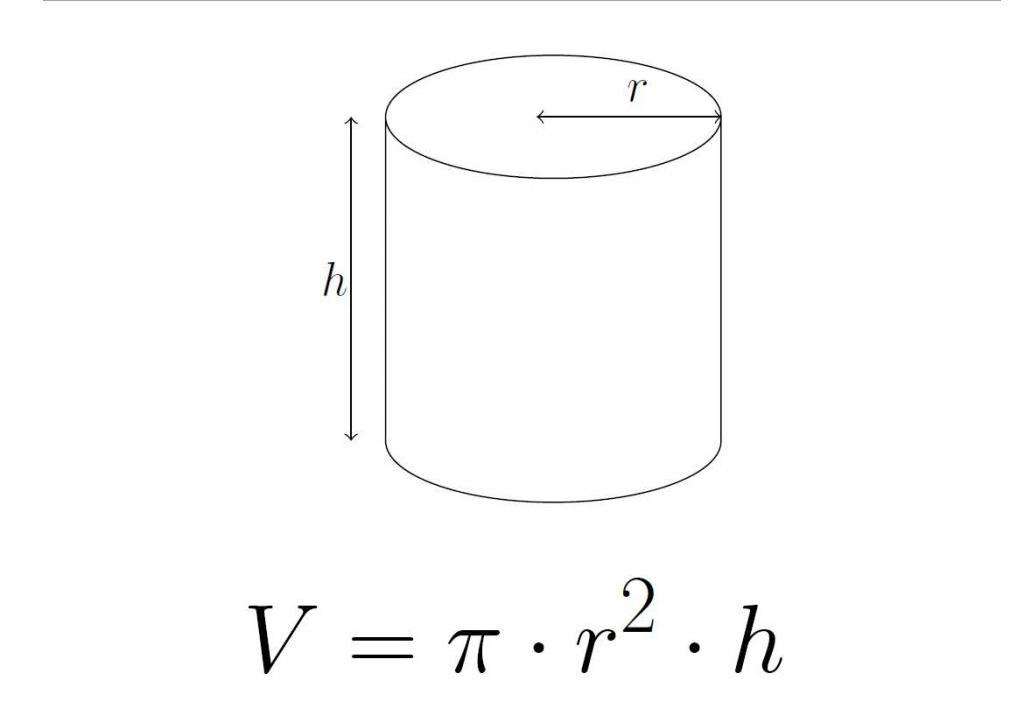При вращении прямоугольника вокруг своей стороны получается геометрическое тело, называемое цилиндром. Данная геометрическая фигура ограничена цилиндрической поверхностью и двумя пересекающими ее параллельными плоскостями — основаниями цилиндра. Радиусом считается отрезок, соединяющий на плоскости основания точку центральной оси цилиндра с точкой его поверхности.
— Если известен объем и высота цилиндра, можно найти его радиус, как корень квадратный из объема деленного на произведение числа пи на высоту цилиндра:
- R = √V / πh
- S (п.п.) = S (б.п.) + 2S (осн.) = 2πrh + πr 2 =πr (2h+r)
- S (б.п.) = hP = 2πrh
- r = S (б.п.) / 2πh
- 2S (осн.) = πr 2
- r = √S (осн.) / π
- S (п.п.) = S (б.п.) + 2S (осн.) = 2πrh + πr 2
- Нахождение радиуса цилиндра: формула и примеры
- Формулы вычисления радиуса цилиндра
- 1. Через объем и высоту
- 2. Через площадь боковой поверхности
- 3. Через полную площадь поверхности
- Примеры задач
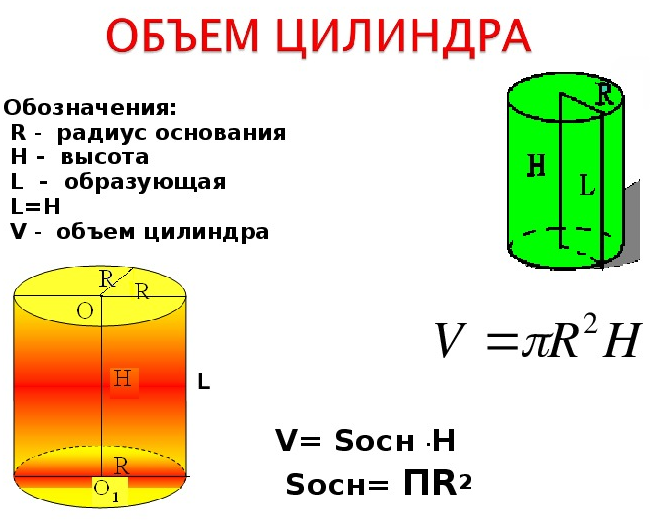
- Объем цилиндра
- Объем правильного цилиндра через радиус и высоту цилиндра
- Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра
- Формулы и калькулятор для вычисления объема цилиндра через диаметр основания
- Объем цилиндрической полости
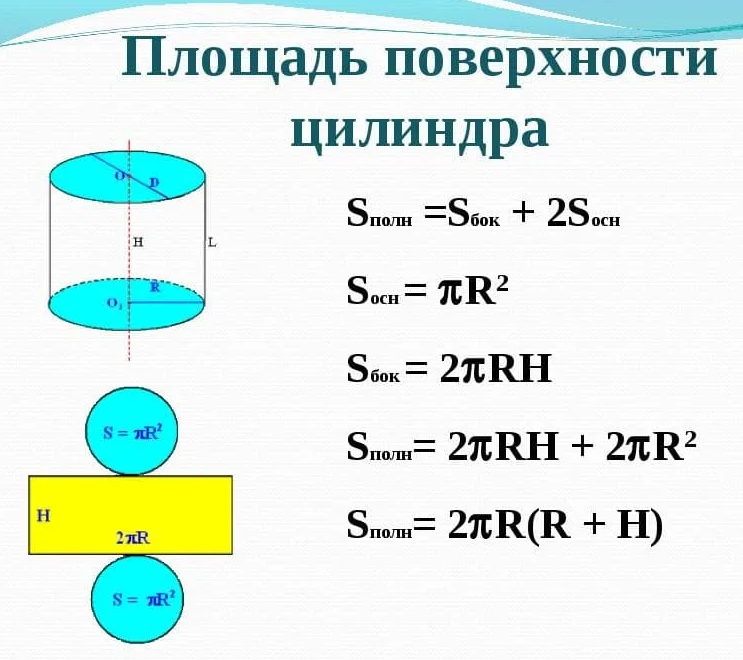
- Поверхности цилиндра
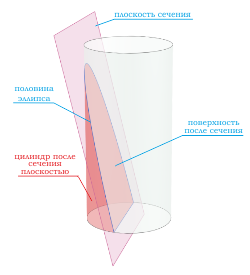
- Сечения цилиндра
- Что такое объем
- Расчет объема цилиндра
- Калькуляторы объема цилиндра
- Формулы для вычисления объема цилиндра
- Примеры решений:
- Нахождение объема цилиндра: формула и задачи
- Формула вычисления объема цилиндра
- Через площадь основания и высоту
- Через радиус основания и высоту
- Через диаметр основания и высоту
- Примеры задач
- Формула объема цилиндра: пример решения задачи
- Объем тел
- Понятие о цилиндре
- Формула объема цилиндра
- Вычисление объема бочки
R = √V / πh
где V — объем цилиндра, h — высота.
Полная площадь поверхности цилиндра складывается из сумм площадей его боковой поверхности и двух оснований:
S (п.п.) = S (б.п.) + 2S (осн.) = 2πrh + πr 2 =πr (2h+r)
Площадь боковой поверхности равняется длине окружности основания умноженной на высоту:
S (б.п.) = hP = 2πrh
— Если известна площадь бок. поверхности S (б.п.) и высота h цилиндра, радиус будет равен частному от деления S (б.п.) на произведение 2пи на высоту:
r = S (б.п.) / 2πh
Площадь двух оснований равна удвоенному произведению пи на радиус в квадрате:
2S (осн.) = πr 2
— Если известна площадь основания и высота, радиус находим как корень квадратный из площади одного основания деленного на пи:
r = √S (осн.) / π
S (п.п.) = S (б.п.) + 2S (осн.) = 2πrh + πr 2
где S (п.п.) — полная площадь поверхности цилиндра; r — радиус; h — высота.
Видео:Видеоурок по математике "Цилиндр"Скачать

Нахождение радиуса цилиндра: формула и примеры
В данной публикации мы рассмотрим, как можно вычислить радиус цилиндра и разберем примеры решения задач для закрепления материала.
Видео:11 класс. Геометрия. Объем цилиндраСкачать

Формулы вычисления радиуса цилиндра
1. Через объем и высоту
Радиус цилиндра рассчитывается по формуле:
V – объем цилиндра; считается как произведение числа π на высоту фигуры на квадрат радиуса круга, являющего ее основанием.
- R – радиус основания цилиндра, т.е. окружности;
- π – число, округленное значение которого равняется 3,14.
2. Через площадь боковой поверхности
Радиус цилиндра считается таким образом:
Sбок. – площадь боковой поверхности цилиндра; равна произведению длины окружности (2 π R), являющейся основанием фигуры, на его высоту:
3. Через полную площадь поверхности
Данная формула получена следующим образом:
S – полная площадь поверхности фигуры, равная:
S = 2 π Rh + 2 π R 2 или S = 2 π R(h + R)
Возьмем первое выражение. Если перенести S в правую часть, получим:
2 π R 2 + 2 π Rh – S = 0
Можно заметить, что это квадратное уравнение вида ax 2 + bx + c = 0, где:
Читайте также: Компрессия во всех цилиндрах ниже
R является корнем данного уравнения (x). Подставив в стандартную формулу для расчета корней наши значения a, b и с получаем*:
* в нашем случае – только один положительный корень, т.к. радиус не может быть отрицательным.
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Примеры задач
Задание 1
Высота цилиндра равняется 5 см, а объем – 141,3 см 3 . Вычислите его радиус.
Решение:
Воспользуемся соответствующей формулой, подставив в нее известные по условиям задачи значения:
Задание 2
Найдите радиус цилиндра, если площадь его боковой поверхности равна 175,84 см 2 , а высота составляет 7 см.
Решение:
Применим формулу, в которой задействованы заданные величины:
Задание 3
Рассчитайте радиус цилиндра, если полная площадь его поверхности – 602,88 см 2 , а высота – 10 см.
Решение:
Используем третью формулу для нахождения неизвестной величины:
Видео:11 класс, 32 урок, Объем цилиндраСкачать

Объем цилиндра
Объем цилиндра, формулы и калькулятор для вычисления объема цилиндра и площади его поверхностей, а также необходимая теория о характеристиках цилиндра.
Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Объем правильного цилиндра через радиус и высоту цилиндра
Видео:Длина окружности. Площадь круга - математика 6 классСкачать

Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра
Видео:Объём цилиндраСкачать

Формулы и калькулятор для вычисления объема цилиндра через диаметр основания
Видео:Радиус и диаметрСкачать

Объем цилиндрической полости
Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.
На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.
Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.
Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.
Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.
Рассмотрим правильный цилиндр.
Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник
Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра.
Радиус основания цилиндра, является радиусом цилиндра.
Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.
Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.
Видео:Объем цилиндраСкачать

Поверхности цилиндра
Наружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая.
Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой.
Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке).
Видео:Объем шара и цилиндра. Практическая часть. 11 класс.Скачать

Сечения цилиндра
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура .
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник , но две боковые стороны которого будут являться кривыми линиями.
Читайте также: Регулятор подачи горючего в цилиндр движка
Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг .
Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс .
Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса .
Видео:Объем цилиндра. Практическая часть. 11 класс.Скачать

Что такое объем
Объем тела (геометрической фигуры) – это количественная характеристика, характеризующая количество пространства, занимаемого телом. Объем выражается в кубических единицах измерения, например: мм 3 , см 3 , мл 3 .
Формула вычисления объема цилиндра часто применяются при расчете массы различных цилиндров, например, прутков, заготовок и т.п. Для вычисления массы, необходимо вычисленный объем цилиндра умножить на плотность материала из которого цилиндр.
Так же, вычислить объём цилиндра иногда требуется для определения полости в виде цилиндра (цилиндрическая полость). В данном случае объём полости будет равен объёму цилиндра, который полностью занимает эту полость.
Объем и площадь других видов цилиндров рассмотрен в статьях:
Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Расчет объема цилиндра
Что бы узнать объем цилиндра вам нужно знать высоту, радиус или площадь, всего есть две основные формулы — площадь основания и высота и радиус и высота.
Самый простой способ это умножить площадь основания цилиндра на его высоту.
Видео:КАК НАЙТИ ОБЪЕМ ШАРА, ЕСЛИ ИЗВЕСТЕН РАДИУС? Примеры | МАТЕМАТИКА 6 классСкачать

Калькуляторы объема цилиндра
- Выберете величины для вычисления — обязательно нужно знать высоту, площадь основания или диаметр цилиндра.
- Для результата введите известные значения величин.
- Выберете нужный показатель результата и вводные в куб. мм, куб. см, куб. м, куб. дюйм.
- Активируйте калькулятор и получите результат (значение не округляются).
Если после использования данного онлайн калькулятора (Расчет объема цилиндра) у вас возникли какие-то вопросы по работе сервиса или вопросы образовательного характера, то Вы всегда можете задать их на нашем форуме.
Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью (называемой боковой поверхностью цилиндра) и не более чем двумя поверхностями (основаниями цилиндра). Цилиндр — круговой если в основании его лежит круг.
Видео:ЕГЭ-2020: Изменение объёма цилиндраСкачать

Формулы для вычисления объема цилиндра
Формула объема цилиндра через радиус и высоту:
Видео:Длина окружности. Математика 6 класс.Скачать

Примеры решений:
Определить, чему равен объем цилиндра, если радиус его основания R равна $225 \pi \mathrm ^ $ , высота равна h в 5 раз болше R.
Вычисляем радиус основания:
Выразим радиус R:
Вычисляем высоту:
Вычисляем объем цилиндра по формуле:
$V=S_ > \cdot h=225 \cdot \pi \cdot 75 \approx 52950 \mathrm > \cdot h=\pi \cdot R^ \cdot h=\pi \cdot 17^ \cdot 140 \approx 127108 \mathrm Источник
Видео:Архимед и объём шараСкачать

Нахождение объема цилиндра: формула и задачи
В данной публикации мы рассмотрим, как можно найти объем цилиндра и разберем примеры решения задач.
Видео:Изменение объема цилиндраСкачать

Формула вычисления объема цилиндра
Через площадь основания и высоту
Объем (V) цилиндра равняется произведению его высоты и площади основания.
Через радиус основания и высоту
Как мы знаем, в качестве оснований цилиндра (равны между собой) выступает круг, площадь которого вычисляется так: S = π ⋅ R 2 . Следовательно, формулу для вычисления объема цилиндра можно представить в виде:
Читайте также: Правило цилиндра в баскетболе что такое
V = π ⋅ R 2 ⋅ H
Примечание: в расчетах значение числа π округляется до 3,14.
Через диаметр основания и высоту
Как нам известно, диаметр круга равняется двум его радиусам: d = 2R. А значит, вычислить объем цилиндра можно следующим образом:
Видео:Объем и площадь поверхности цилиндра (видео 44) | Подобие. Геометрия | МатематикаСкачать

Примеры задач
Задание 1
Найдите объем цилиндра, если дана площадь его основания – 78,5 см 2 , а также, высота – 10 см.
Решение:
Применим первую формулу, подставив в нее известные значения:
V = 78,5 см 2 ⋅ 10 см = 785 см 3 .
Задание 2
Высота цилиндра равна 6 см, а его диаметр – 8 см. Найдите объем фигуры.
Решение:
Воспользовавшись третьей формулой, в которой участвует диаметр, получаем:
V = 3,14 ⋅ (8/2 см) 2 ⋅ 6 см = 301,44 см 3 .
Видео:Задание 2|ЕГЭ ПРОФИЛЬ| СТЕРЕОМЕТРИЯ| Цилиндр вписан в прямоугольный параллелепипед.Радиус основанияСкачать

Формула объема цилиндра: пример решения задачи
Объем является физической величиной, которая присуща телу с ненулевыми размерами вдоль каждого из трех направлений пространства (все реальные объекты). В статье в качестве примера формулы объема рассматривается соответствующее выражение для цилиндра.
Видео:Цилиндр, конус, шар, 6 классСкачать

Объем тел
Эта физическая величина показывает, какую часть пространства занимает то или иное тело. Например, объем Солнца намного больше этой величины для нашей планеты. Это означает, что принадлежащее Солнцу пространство, в котором находится вещество этой звезды (плазма), превышает земную пространственную область.
Объем изменяется в кубических единицах длины, в СИ это метры в кубе (м3). На практике объемы жидких тел измеряют в литрах. Маленькие объемы могут выражать в кубических сантиметрах, миллилитрах и других единицах.
Для вычисления объема формула будет зависеть от геометрических особенностей рассматриваемого объекта. Например, для куба это тройное произведение длины его ребер. Ниже рассмотрим фигуру цилиндр и ответим на вопрос о том, как найти объем его.
Понятие о цилиндре
Фигура, о которой пойдет речь, является достаточно непростой. Согласно геометрическому определению, она представляет собой поверхность, образованную путем параллельного перемещения прямой (генератрисы) вдоль некоторой кривой (директрисы). Генератриса также называется образующей, а директриса — направляющей.
Если директриса — это окружность, а генератриса перпендикулярна ей, тогда полученный цилиндр называют круглым и прямым. О нем и пойдет дальше речь.
Цилиндр имеет два основания, которые параллельны друг другу и соединены цилиндрической поверхностью. Проходящая через центры двух оснований прямая называется осью круглого цилиндра. Все точки фигуры находятся на одинаковом расстоянии от этой прямой, которое равно радиусу основания.
Круглый прямой цилиндр однозначно определяется двумя параметрами: радиусом основания (R) и расстоянием между основаниями — высота H.
Формула объема цилиндра
Для расчета области пространства, которую занимает цилиндр, достаточно знать его высоту H и радиус основания R. Искомое равенство в этом случае имеет вид:
Понять эту формулу объема просто: поскольку высота перпендикулярна основаниям, то если ее умножить на площадь одного из них, получается нужная величина V.
Вычисление объема бочки
Для примера решим такую задачу: определим, сколько воды поместится в бочку, имеющую диаметр дна 50 см и высоту 1 метр.
Радиус бочки равен R=D/2=50/2=25 см. Подставляем данные в формулу, получаем:
V = pi*R2*H = 3,1416*252*100 = 196350 см3
Поскольку 1 л = 1 дм3 = 1000 см3, то получаем:
V = 196350/1000 = 196,35 литра.
То есть в бочку можно налить почти 200 литров воды.