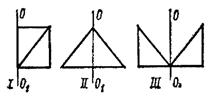Как изменится момент инерции свинцового цилиндра (8 видео)

Из сплошного однородного цилиндра сделали полый, удалив половину массы. Как изменился момент инерции цилиндра относительно его оси?
а) уменьшился в 2 раза
б) уменьшился более чем в 2 раза
и) уменьшился менее чем в 2 раза
г) остался неизменным
д) стал равным нулю.

Я думаю что он уменьшился в 2 раза, т.к после удаления половины цилиндра момент инерции стал равен
I=mR^2/4
Я правильно рассуждаю?

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Чему равен момент инерции полого цилиндра?
Чему равен момент инерции полого цилиндра относительно осей, x, y, z? Чему равен момент инерции.

Найти момент инерции I и момент импульса земного шара относительно оси вращения
Найти момент инерции I и момент импульса земного шара относительно оси вращения.Масса Земли равна.

Определить момент силы торможения, если момент инерции маховика равен 1кг/м^2
маховик делал 10 оборотов в секунду,при торможении он остановился,сделав 30 оборотов от начало.

Найти момент инерции J вентилятора и момент сил торможения
Вентелятор вращается с частотой n=900 об/мин. После выключения вентилятор, вращаясь равно.

Приведу формулы, по которым можно сделать выводы относительно изменения момента инерции цилиндра.
И так:
момент инерции сплошного однородного цилиндра относительно оси цилиндра

момент инерции полого цилиндра(обруча) с внутренним и внешним радиусом относительно оси цилиндра

момент инерции тонкостенного полого цилиндра(можно принять )

Добавлено через 13 минут
В общем случае, если ось цилиндра направить вдоль оси oz, то момент инерции цилиндра вдоль оси oz вычисляется через тройной интеграл

где — объемная плотность, которая непрерывно распределена по объему цилиндра.

Содержание

Законы сохранения и симметрия пространства и времени
Как изменится момент инерции свинцового цилиндра
Момент инерции цилиндра сплошного и полого относительно разных осей. Пример задачи
Что такое момент инерции?
Сплошной цилиндр и главная ось
Однородный цилиндр и перпендикулярная генератрисе ось
Полый цилиндр
Где используются знания величин I для цилиндров?
Пример решения задачи
💡 Видео

Видео:Момент инерцииСкачать

Законы сохранения и симметрия пространства и времени

Закон сохранения энергии является следствием однородности времени, закон сохранения импульса – следствием однородности пространства, а закон сохранения момента импульса – следствием изотропии пространства.

Однородность времени означает, что если в два любых момента времени все тела замкнутой системы поставить в совершенно одинаковые условия, то начиная с этих моментов все явления в ней будут протекать совершенно одинаково.

Однородность пространства означает, что если замкнутую систему тел перенести из одного места пространства в другое, поставив при этом все тела в ней в те же условия, в каких они находились в прежнем положении, то это не отразится на ходе всех последующих явлений.

В том же смысле надо понимать и изотропию пространства, только вместо переноса замкнутой системы надо говорить об ее повороте в пространстве на любой угол.

1. Может ли обладать моментом импульса материальная точка, движущаяся по прямолинейной траектории?

2. От каких величин зависит угловое ускорение твердого тела?

3. В каком случае кинетическая энергия вращающегося тела определяется формулой ?

4. Найдите кинетическую энергию катящегося без проскальзывания однородного шара массы М, если скорость его центра масс равна V_c. Как изменится результат, если вместо шара катится однородный цилиндр?

1. Катушка покоится на горизонтальной плоскости. В каком направлении покатится катушка, если нить потянуть в направлении I? в направлении II? Качение происходит без проскальзывания. 1)®, ¬; 2)¬, ¬; 3)®,¬; 4)¬,®.

2. Справедливо ли выражение момента инерции тел I = mr 2 (т – масса тела) относительно оси в следующих случаях: а) тело – материальная точка, r – расстояние ее до оси; б) тело – однородный шар, r – расстояние центра шара до оси; в) тело произвольное, r – расстояние центра масс тела до оси?

3. Как изменится момент инерции свинцового цилиндра относительно его оси, если цилиндр сплющить в диск?

Читайте также: Диаметр главного тормозного цилиндра уаз 469

4. Из сплошного однородного цилиндра сделали полый, удалив половину массы. Как изменился момент инерции цилиндра относительно его оси? Уменьшился: 1) в 2 раза; 2) больше, чем в 2 раза; 3) меньше, чем в 2 раза.

5. На рисунке изображены тела, составленные из одинаковых однородных треугольных пластин. Указать фигуры с минимальным и максимальным моментами инерции относительно оси ОО₁.

1) I, II; 2) I, III; 3) II, III; 4) III, II; 5) III, I.

6. Как изменится момент инерции двух материальных точек массами m, если ось ОО₁ перевести: а) в положение I; б) в положение II?

7. Два диска одинаковой толщины с равными массами, железный и деревянный, вращаются под действием равных по модулю сил, касательных к ободам дисков. Сравнить угловые ускорения дисков.

8. Качается однородный стержень длиной l и массой m. Ось качаний проходит через конец стержня и расположена горизонтально. Какую длину должен иметь математический маятник массой m, чтобы при равных углах отклонения от вертикали оба маятника имели одинаковы угловые ускорения? 1) l;2) l/2;3) 3l/2;4) 2l/3;5) l/6.

9. С наклонной плоскости одновременно начинают скатываться без проскальзывания цилиндры: а) сплошной б) тонкостенный полый. Найти отношение скоростей (u_a/u_b) в данный момент времени.

1) 2; 2) ; 3) ; 4) ; 5) недостаточно данных.

10. Два диска с равными массами и радиусами R₁ и R₂ (R₂ = 2R₁) раскручивают из состояния покоя до одинаковых угловых скоростей. Найти отношение произведенных работ (A₁/A₂).

11. С горки с одной и той же высоты скатываются без проскальзывания два цилиндра: а) сплошной; б) тонкостенный полый. Найти отношение их скоростей в одном и том же месте (u_a/u_b).

1) ; 2) ; 3) 2; 4) недостаточно данных.

12. Падает шест массой m, высотой Н. Найти скорость υ верхнего конца шеста в момент падения на землю. Нижний конец шеста не проскальзывает. Верны ли приведенные этапы решения: a) ; б) u = wH; в) Iw 2 /2 = mgH,

13. По наклонной плоскости с одной и той же высоты спускается обруч:

а) скользя без качения с пренебрежимо малым трением;

б) катясь без проскальзывания. Найти отношение скоростей центра колеса в одном и том же месте (u_a/u_b).

1) ; 2) 2; 3) 4; 4) ; 5) .

14. Можно ли утверждать, что в неизолированной системе сохраняются: а) импульс, если сумма внешних сил равна нулю; б) момент импульса относительно оси, если сумма моментов внешних сил относительно этой оси равна нулю; в) механическая энергия, если работа внешних сил равна нулю?

15. Человек, стоящий на вращающейся скамье Жуковскоого, держит в руках гири. В некоторый момент человек выпускает гири из рук. Как изменилась угловая скорость скамьи?

Видео:Урок 94. Вычисление моментов инерции телСкачать

Как изменится момент инерции свинцового цилиндра

Определить момент инерции J кольца массой m = 50 г и радиусом R = 10 см относительно оси, касательной к кольцу.

Определите момент инерции стального маховика относительно оси вала. Плотность стали ρ = 7800 кг/м 3 , радиус центрального отверстия для вала r = 0,1 м, R₁ = 6r, R₂ = 4r, R₃ = 2r, α = 45°. Плоский маховик толщиной h = 0,02 м с цилиндрическими вырезами. Количество вырезов n найдите по формуле п = 360/α, их радиусы равны r.

Определите момент инерции стального маховика относительно оси вала. Плотность стали ρ = 7800 кг/м 3 , радиус центрального отверстия для вала r = 0,1 м, R₁ = 6r, R₂ = 4r, R₃ = 2r, α = 180°. Маховик с шарами на спицах. Количество шаров п найдите по формуле n = 360/α, их радиусы равны r, длина втулки равна 0,02 м. Массами спиц пренебречь.

Определите момент инерции стального маховика относительно оси вала. Плотность стали ρ = 7800 кг/м 3 , радиус центрального отверстия для вала r = 0,1 м, R₁ = 6r, R₂ = 4r, R₃ = 2r, α = 45°. Плоский маховик толщиной h = 0,02 м с двумя симметричными вырезами.

Читайте также: Главный тормозной цилиндр погрузчика львовского

Фигурист вращается, делая 6 об/с. Как изменится момент инерции фигуриста, если он прижмет руки к груди и при этом частота вращения станет 18 об/с.

Определить момент инерции кольца массой m = 250 г и радиусом R = 10 см относительно оси, касательной к кольцу.

На рисунке приведены зависимости кинетической энергии W вр трех вращающихся тел от квадрата угловой скорости ω 2 . Какому графику соответствует наибольший момент инерции тела? Поясните свой ответ.

На рисунке приведены зависимости кинетической энергии трех вращающихся тел W_вр от квадрата угловой скорости ω 2 . Какому графику соответствует наименьший момент инерции тела? Укажите его номер и поясните свой выбор.

На рисунке приведена зависимость модуля моментов сил, приложенных к разным телам, от модуля углового ускорения тел. Наибольший момент инерции имеет тело под номером

Момент силы, приложенный к вращающемуся телу, изменяется по закону M = M₀ – αt, где α — некоторая положительная константа. Момент инерции остается постоянным в течение всего времени вращения. Зависимость углового ускорения от времени представлена на рисунке .
.

Момент силы, приложенный к вращающемуся телу, изменяется по закону M = αt 2 , где α — некоторая положительная константа. Момент инерции остается постоянным в течение всего времени вращения. Зависимость углового ускорения от времени представлена на рисунке .
.

Момент силы, приложенный к вращающемуся телу, изменяется по закону M = M₀ – αt 2 , где α — некоторая положительная константа. Момент инерции остается постоянным в течение всего времени вращения. Зависимость углового ускорения от времени представлена на рисунке .
.

Маховик вращается по закону, выражаемому уравнением φ = А+Вt+Сt 2 , где А = 3 рад, В = 28 рад/с, С = – 5 рад/с 2 . Найти среднюю мощность , развиваемую силами, действующими на маховик при его вращении, до остановки, если его момент инерции J = 100 кг×м 2 .

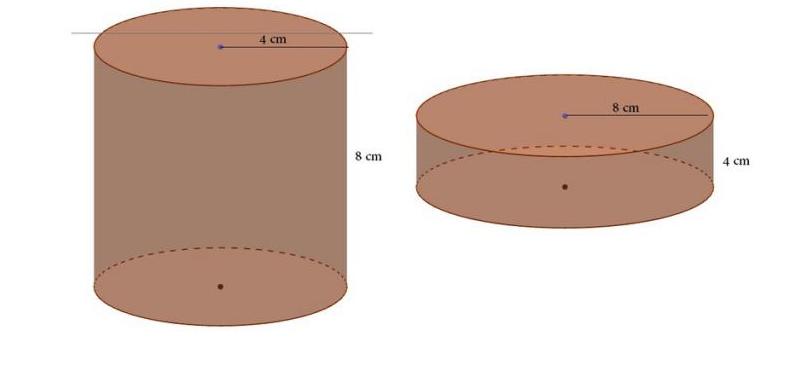
Полый цилиндр массой 8 кг имеет внутренний диаметр 1 м, внешний 1,1 м. Чему равен момент инерции этого цилиндра относительно своей оси?

Шарик радиуса 6,2 см из пластичного материала имеет некоторый момент инерции I₁. Этот шарик преобразуют в цилиндр высоты 3,8 см. Момент инерции цилиндра относительно его оси оказался I₂. Найти отношение I₂/I₁.

Видео:Расчет момента инерции цилиндраСкачать

Момент инерции цилиндра сплошного и полого относительно разных осей. Пример задачи

Как известно, масса в динамике поступательного движения играет важную роль, определяя инерционные свойства движущихся тел. В динамике вращения вместо массы пользуются моментом инерции. Рассмотрим в статье, что это за величина и как определяется момент инерции цилиндра относительно оси.

Видео:Зависимость углового ускорения от момента инерцииСкачать

Что такое момент инерции?

Эту величину обычно обозначают буквой I. Для материальной точки математическая формула момента инерции записывается так:

Где r — расстояние до оси вращения от точки массой m. Из формулы понятно, что единицей измерения величины являются килограммы на квадратный метр (кг*м 2 ).

Если тело имеет сложную форму и его объемная плотность является переменной, тогда для определения I следует использовать такое интегральное выражение:

Где dm — это элементарная масса, находящаяся от оси вращения на расстоянии r.

Таким образом, момент инерции определяет распределение материи в теле сложной формы относительно конкретной оси вращения системы.

Видео:2 а Моменты инерции сферы и шараСкачать

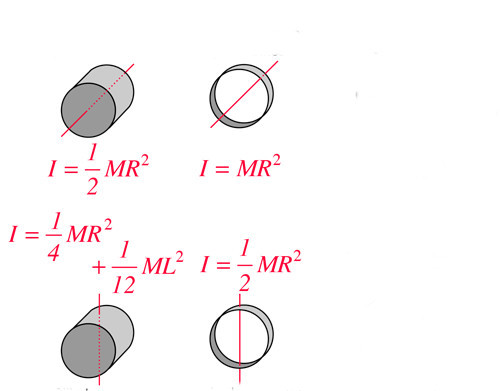
Сплошной цилиндр и главная ось

Момент инерции сплошного цилиндра может быть вычислен вокруг абсолютно любой оси с использованием интегрального выражения, записанного в предыдущем пункте. Здесь рассмотрим ситуацию, когда цилиндр массой M, радиусом R и высотой L вращается вокруг главной оси. Последняя представляет собой прямую, параллельную генератрисе фигуры и проходящую через центры ее круглых оснований.

Не будем вдаваться в подробности математических вычислений по интегральной формуле, а приведем сразу конечное выражение:

Мы видим, что чем больше масса цилиндра и его радиус, тем больше момент инерции I₁. В то же время эта величина никак не зависит от высоты фигуры L, то есть момент инерции тонкого диска можно вычислить также по этой формуле.

Отметим, что если всю массу цилиндра собрать в одну материальную точку, находящуюся от оси вращения на расстоянии радиуса R, то для нее момент инерции окажется в два раза больше, чем для сплошного цилиндра.

Читайте также: Задний тормозной цилиндр рено сандеро степвей 2013

Видео:Расчет момента инерции диска или цельного цилиндраСкачать

Однородный цилиндр и перпендикулярная генератрисе ось

Теперь возьмем однородный цилиндр из примера выше и перевернем его на бок. Начнем вращать объект вокруг оси, которая проходит также через центр его масс, но уже перпендикулярна генератрисе (главной оси). Чему будет равен момент инерции цилиндра однородного в данном случае?

Как и в примере выше, здесь также ограничимся приведением соответствующего выражения. Оно будет иметь следующий вид:

Момент инерции I₂ имеет более сложную зависимость от параметров цилиндра, чем I₁, поскольку он определяется не только массой и радиусом, но и высотой фигуры. Заметим, что два слагаемых этой формулы представляют собой два крайних случая:

Если цилиндр слишком маленькую высоту имеет, то мы получаем диск, который, вращаясь вокруг оси, проходящей через его диаметр, будет иметь момент 1/4*M*R 2 .
Если радиус цилиндра стремится к нулю, то рассматриваемый объект превратится в стержень, и его момент инерции станет равным 1/12*M*L 2 .

Видео:момент инерции цилиндраСкачать

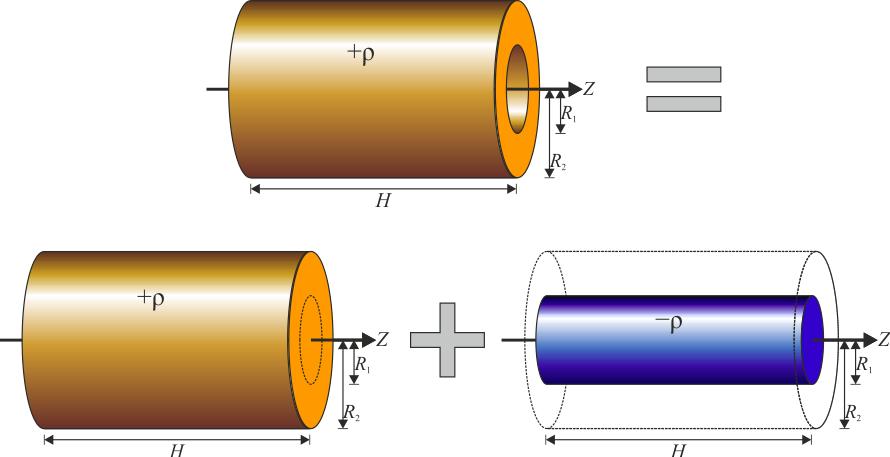
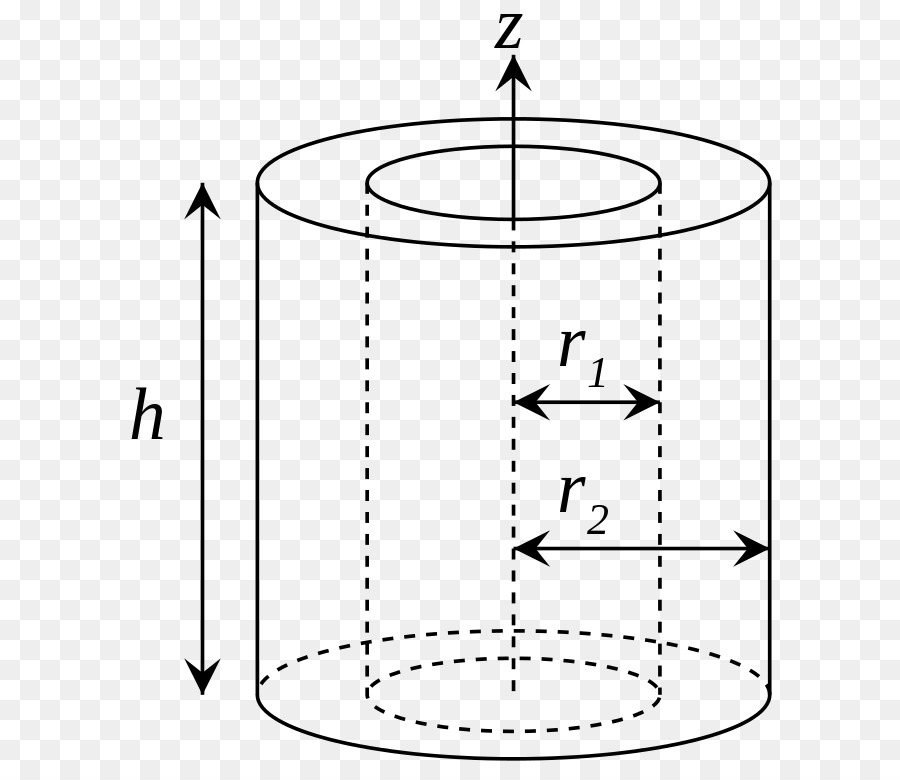
Полый цилиндр

Выше мы рассмотрели, как рассчитывать момент инерции цилиндра вращающегося и однородного. Теперь предположим, что высота цилиндра и его масса остались теми же самыми, однако он стал полым, то есть, имеет два радиуса: внешний R₁ и внутренний R₂.

Применение все той же интегральной формулы позволяет получить выражение для момента инерции цилиндра полого, который вращается вокруг своей главной оси. Соответствующая формула выглядит так:

Это выражение позволяет сделать важный вывод: при одинаковых массах полого и сплошного цилиндров первый обладает большим моментом инерции. Связан этот факт с тем, что большая часть массы полого цилиндра находится дальше от оси вращения, а как видно из формул, от радиуса изучаемая величина растет квадратично.

Видео:Расчёт момента инерции тела относительно оси вращения. Момент инерции однородного стержняСкачать

Где используются знания величин I для цилиндров?

Пожалуй, основной областью применения изложенной выше теории является автомобильная промышленность. В частности, коленчатый вал автомобиля снабжен тяжелым сплошным маховиком, имеющим цилиндрическую форму. Необходим маховик для того, чтобы обеспечить максимальную плавность вращения коленчатого вала, что отражается на плавности автомобильного хода. Маховик гасит любые большие угловые ускорения как во время разгона транспортного средства, так при его торможении.

Из формулы выше для момента инерции I₁ понятно, что для увеличения этой величины выгоднее увеличить радиус, чем массу цилиндра (маховика). Так, удвоение массы приведет лишь к удвоению момента инерции. Однако если увеличить в два раза радиус, то I₁ возрастет аж в 4 раза, что обеспечит более эффективное использование маховика.

Видео:Расчет момента инерции шараСкачать

Пример решения задачи

Прежде чем решать задачу, скажем несколько слов о динамике вращения. Как и в динамике поступательного движения, в ней существует формула, подобная второму закону Ньютона. Эта формула называется уравнением моментов. Записывается она так:

Где L — момент импульса, M — момент внешних сил. Чаще всего это уравнение записывают в следующем виде:

Здесь α — ускорение угловое. Из этого выражения видна аналогия со вторым ньютоновским законом.

Теперь перейдем к решению задачи. Известно, что сила в 100 Н действует по касательной к цилиндрической поверхности перпендикулярно главной оси вращения сплошного цилиндра на расстоянии 20 см. Масса цилиндра равна 10 кг, а его радиус составляет 20 см. Необходимо определить угловую скорость ω цилиндра через 5 секунд после начала действия силы.

Угловая скорость рассчитывается по формуле для равноускоренного движения:

Выражая ускорение из уравнения моментов и подставляя его в выражение, получим:

Момент силы вычисляется так:

Где по условию задачи d = R. Подставляя это выражение и выражение для I сплошного цилиндра, получим конечную рабочую формулу:

Осталось сюда подставить все величины в единицах СИ и записать ответ: ω = 500 рад/с, что равно приблизительно 80 оборотам в секунду.