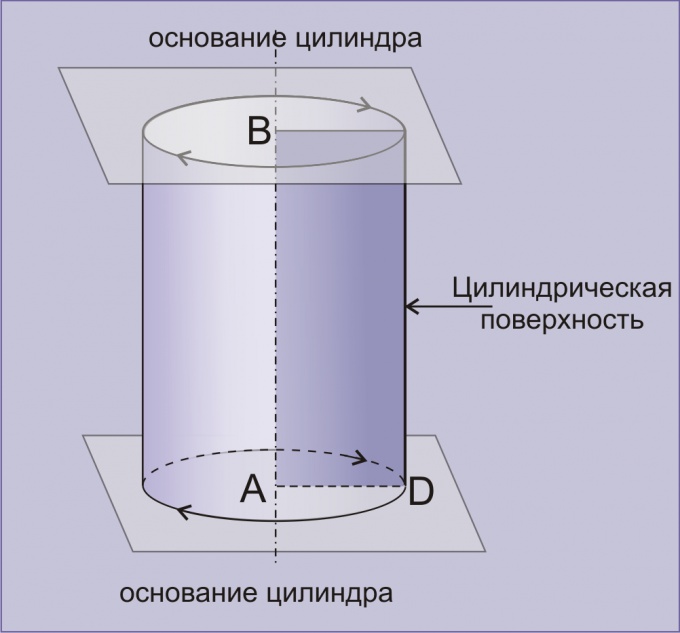
Со школьной скамьи все мы знаем, что цилиндр — это геометрическое тело, которое образовано цилиндрической поверхностью и 2-мя параллельными плоскостями. Цилиндр, который образуется в результате вращения обыкновенного прямоугольника вокруг одной из своих сторон, называется прямым. Вычислить объем такого цилиндра достаточно просто. Для этого вам понадобится: обычная школьная линейка (или рулетка), простой карандаш и прямоугольный лист бумаги или школьного картона.
- Объем цилиндра формула
- Как найти объема цилиндра
- Как найти объем цилиндра: формула через диаметр и высоту
- Объем цилиндра
- Объем цилиндра формула (через радиус основания и высоту)
- Зная радиус r и высоту h
- Формула
- Пример
- Зная диаметр d и высоту h
- Формула
- Пример
- Формула вычисления объема цилиндра
- Введите радиус основания и высоту цилиндра
- Примеры задач
- Поэтапный расчет объема картонной коробки
- Подсчет объема коробки в литрах
- Объем цилиндрической полости
- Объем прямого цилиндра
- Объем цилиндра через площадь основания и высоту цилиндра
- Поверхности цилиндра
- Сечения цилиндра
- Как рассчитать объем цилиндра с помощью калькулятора
- 🔥 Видео
Видео:Объём цилиндраСкачать

Объем цилиндра формула
1. К примеру, у вас есть бочка цилиндрической формы, которую необходимо наполнить жидкостью. Для того чтобы определить необходимое количество жидкости, вам нужно предварительно просчитать объем бочки.
Формула, благодаря которой можно определить объем цилиндра имеет такой вид:
где S – площадь основания цилиндра;
Н – его высота (ее можно измерить с помощью линейки или рулетки).
2. Теперь необходимо определить площадь основания нашего цилиндра. Формула, согласно которой можно рассчитать площадь круга, имеет такой вид:
Где п – число равное приблизительно 3,14;
R – радиус исходной окружности.
Определить площадь окружности при помощи одной лишь линейки достаточно просто.
Как известно, вписать прямоугольный треугольник можно в любую окружность. А гипотенуза такого треугольника будет равна диаметру описанной вокруг него окружности.
Для того, чтобы измерить диаметр нашей бочки, берем лист картона (или бумаги) и располагаем его таким образом, чтобы вершина прямого угла касалась края окружности.
При помощи карандаша помечаем стороны, которые соприкасаются с окружностью, а затем соединяем их прямой линией. Данный отрезок и будет являться диаметром основания нашей бочки. Делим отрезок на две одинаковые части (каждая из которых будет равна радиусу окружности) и подставляем полученное значение в исходную формулу.
Видео:Цилиндр - расчёт площади, объёма.Скачать

Как найти объема цилиндра
- • Линейка или рулетка.
- • Карандаш или маркер.
- • Лист бумаги или картона или другой подходящий предмет с прямыми углами.
Предположим, у вас есть некая емкость для воды цилиндрической формы. Вам надо ее заполнить водой, но для этого вы хотите вычислить объем, который она заполнит.
Из школьного курса геометрии вы знаете, что формула объема цилиндра выглядит так:
что значит, объем цилиндра равен произведению площади основания S на его высоту H.
Высоту цилиндра H измеряем легко рулеткой или линейкой.
Теперь определим площадь основания. Площадь круга, как нам тоже известно из школьной геометрии, определяется по формуле:
Читайте также: Тормозной цилиндр ниссан патрол y62
где π – число, обозначающее в математике соотношение длин окружности и диаметра и равное 3.14159265…,
Как можно вычислить площадь окружности, имея под рукой только линейку? Очень просто!
Из того же школьного курса геометрии вспомним, что в любую окружность можно вписать прямоугольный треугольник. Причем, гипотенуза этого треугольника будет равна диаметру данной окружности.
Для этого берем лист картона или другой подходящий предмет, имеющий прямые углы и накладываем на наш цилиндр так, чтобы прямой угол α своей вершиной А упирался в край цилиндра.
Стороны прямоугольника, которые пересекаются с окружностью, помечаем карандашом или маркером и соединяем прямой линией. В нашем случае это вершины треугольника В и С. Этот отрезок и есть диаметр нашей окружности. Радиус окружности равен половине ее диаметра. Делим отрезок ВС на две части. Центром окружности является точка О. Отрезки ОВ и ОС равны и являются радиусом основания данного цилиндра. Теперь подставляем полученные значения в формулу:
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Как найти объем цилиндра: формула через диаметр и высоту
Видео:11 класс. Геометрия. Объем цилиндраСкачать

Объем цилиндра
Объем цилиндра равен произведению площади его основания на высоту.
Видео:Объем цилиндраСкачать

Объем цилиндра формула (через радиус основания и высоту)
r — радиус основания цилиндра,
Если внимательно посмотреть на эту формулу, то можно заметить, что
— это формула площади круга, а в нашем случае — площадь основания. Поэтому формулу объема цилиндра можно записать через площадь основания и высоту:
Зная радиус r и высоту h
Чему равен объем цилиндра V если известны его радиус r и высота h?
Формула
Пример
Если цилиндр имеет высоту h = 8 см, а его радиус r = 2 см, то:
V = 3.14156 ⋅ 2 2 ⋅ 8 = 3.14156 ⋅ 32 = 100.53 см 3
Зная диаметр d и высоту h
Чему равен объем цилиндра V если известны его диаметр d и высота h?
Формула
Пример
Если цилиндр имеет высоту h = 5 см, а его диаметр d = 1 см, то:
V = 3.14156 ⋅ ( 1 /2) 2 ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см 3
Видео:Видеоурок по математике "Цилиндр"Скачать

Формула вычисления объема цилиндра
1. Через площадь основания и высоту
Объем (V) цилиндра равняется произведению его высоты и площади основания.
2. Через радиус основания и высоту
Как мы знаем, в качестве оснований цилиндра (равны между собой) выступает круг, площадь которого вычисляется так: S = π ⋅ R 2 . Следовательно, формулу для вычисления объема цилиндра можно представить в виде:
V = π ⋅ R 2 ⋅ H
Примечание: в расчетах значение числа π округляется до 3,14.
3. Через диаметр основания и высоту
Как нам известно, диаметр круга равняется двум его радиусам: d = 2R. А значит, вычислить объем цилиндра можно следующим образом:
V = π ⋅ (d/2) 2 ⋅ H
Видео:Сколько в бочке литров? Посчитаем.Скачать

Введите радиус основания и высоту цилиндра
Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Читайте также: Как использовать массажный цилиндр
, где R – радиус оснований, h – высота цилиндра
Видео:Как измерить цилиндр рулеткой!?Скачать

Примеры задач
Задание 1
Найдите объем цилиндра, если дана площадь его основания – 78,5 см 2 , а также, высота – 10 см.
Решение:
Применим первую формулу, подставив в нее известные значения:
V = 78,5 см 2 ⋅ 10 см = 785 см 3 .
Задание 2
Высота цилиндра равна 6 см, а его диаметр – 8 см. Найдите объем фигуры.
Решение:
Воспользовавшись третьей формулой, в которой участвует диаметр, получаем:
V = 3,14 ⋅ (8/2 см) 2 ⋅ 6 см = 301,44 см 3 .
Видео:Объём цилиндраСкачать

Поэтапный расчет объема картонной коробки
- Измерить длину а и ширину b, если дно коробки квадратное, то а=b; Измерить высоту h как расстояние от нижнего до верхнего клапана коробки.
Сначала нужно рассчитать внутренний объем коробки, необходимый для размещения груза. Габаритные размеры груза должны быть на 5–10 мм меньше, чем внутренние размеры гофроупаковки.
V=a*b*h
где a – длина основания (м), b – ширина основания (м),
h – высота коробки (м).
V=S*h
где S — площадь основания коробки, а h — ее высота.
Объем, занимаемый заготовкой (коробкой) (с учетом толщины стенок) рассчитывается для правильного размещения внутри транспортного средства или хранения на складе.
Формула для расчета занимаемого объема:
V=Площадь (S) * толщину листа
*как рассчитать площадь (S) картонной коробки — в этой статье
| Тип: | Профиль: | Толщина (мм): |
| Трехслойный гофрокартон | B | 3 |
| Трехслойный гофрокартон | C | 3,7 |
| Трехслойный гофрокартон | E | 1,6 |
| Пятислойный гофрокартон | BC | 7 |
| Пятислойный гофрокартон | BE | 4 |
Перемножив полученные значения, получим объем коробки в кубических метрах. Чтобы получить результат в литрах необходимо полученное значение в м 3 умножить на 1000.
Видео:Объем цилиндра.Скачать

Подсчет объема коробки в литрах
При транспортировке мелких или сыпучих товаров их также пакуют в ящики. Учитывая, что такие предметы и материалы занимают весь объем тары, нужно знать их количество в литрах. Если Вы интересуетесь, как посчитать объем короба в литрах, определяйте литраж следующим образом:
находим кубатуру V=a*b*h =0,3*0,25*0,15=0,0112 м 3 ;
зная равенство: 1 м 3 = 1000 л, переводим полученное значение в литры: V=0,0112 *1000=1,2 л.
Видео:11 класс, 32 урок, Объем цилиндраСкачать

Объем цилиндрической полости
Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.
На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.
Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.
Цилиндр может быть правильным или наклонным
Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.
Читайте также: Цилиндр для бензопилы partner
Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.
Рассмотрим правильный цилиндр.
Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник
Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра.
Радиус основания цилиндра, является радиусом цилиндра.
Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.
Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.
Видео:Измерение штангенциркулем (job4man.ru).MOVСкачать

Объем прямого цилиндра
Цилиндр – это геометрическое тело, которое сформировано вращением прямоугольника на оси, совпадающей с одним из его сторон. Слово «цилиндр» происходит от греческого слова «kylindros».
Объем цилиндра через площадь основания и высоту цилиндра
Объем цилиндра равен произведению площади основания цилиндра на его высоту.
где:
V – объем цилиндра
H – высота цилиндра
S – площадь цилиндра
Видео:Объем цилиндра.Скачать

Поверхности цилиндра
Наружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая.
Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой.
Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке).
Видео:Объем цилиндра. Практическая часть. 11 класс.Скачать

Сечения цилиндра
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник , но две боковые стороны которого будут являться кривыми линиями.
Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг
Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс
Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса
Видео:Длина окружности. Математика 6 класс.Скачать

Как рассчитать объем цилиндра с помощью калькулятора
Калькулятор позволяет определить объем цилиндра по одному из 3 вариантов:
- площадь основания и высота цилиндра;
- радиус основания и высота цилиндра;
- диаметр основания и высота цилиндра.
Выберите соответствующий шаг и введите исходные данные в соответствующие поля.
Также важно указать единицы измерения по условиям задачи.
Расчеты будут выполнены автоматически и конвертированы в основные метрические физические величины объема.
🔥 Видео
Объем цилиндра. Урок 13. Геометрия 11 классСкачать

Вычисление объёма цилиндраСкачать

Длина окружности. Площадь круга - математика 6 классСкачать

КАК ИЗМЕРИТЬ ЦИЛИНДРЫ? Учимся пользоваться нутромером и микрометромСкачать

Как начертить цилиндр в объемеСкачать