Как начертить конус цилиндр (5 видео)

Поскольку круги, лежащие в основаниях цилиндра и конуса, расположены параллельно горизонтальной плоскости проекций Я, то их проекции на эту плоскость будут также кругами. Фронтальная и профильная проекции цилиндра — прямоугольники, а конуса — равнобедренные треугольники.

Проекции конуса отличаются от проекций цилиндра только тем, что содержат равнобедренные треугольники вместо прямоугольников.

Дан чертеж усеченного конуса. Его горизонтальная проекция представляет собой два круга, а фронтальная проекция — равнобочную трапецию.

Заметьте, что на всех проекциях следует наносить оси симметрии, с проведения которых и начинают выполнение чертежей цилиндра и конуса.

Видно, что фронтальная и профильная проекции цилиндра одинаковы. То же можно сказать о проекциях конуса. Поэтому в данном случае профильная проекция на чертеже лишняя.

Размеры цилиндра и конуса определяются их высотой h и диаметром основания d. Для усеченного конуса указывают высоту h и диаметры обоих оснований D и d.

Обратите внимание, что знак 0 позволяет определять форму предмета при чтении чертежа и но одной проекции.

проводят оси х и у, на которых строят ромб со стороной, равной диаметру предмета; rn
в ромб вписывают овал; rn
вдоль оси г откладывают высоту предмета. Для цилиндра и усеченного конуса строят второй овал; rn
проводят касательные к овалам. rn

rnОтветьте на вопросы

Какие фигуры получаются при проецировании цилиндра? rn
Какие фигуры получаются при проецировании полного конуса? rn
Какие размеры наносят па чертежах цилиндра и полного конуса? rn
Что означает знак 0 перед размерным числом? rn

Расположите перед собой шашку или монету так, чтобы они соответствовали чертежам. rn
Сложите из брусков, имеющих форму прямоугольного параллелепипеда, и цилиндров предметы. rn

Содержание

Чертежик
Метки
Пересечение конуса и цилиндра пошаговое выполнение
Как начертить конус цилиндр
Пошаговое решение задачи №9 — построение развертки конуса и цилиндра (Фролов / Бубенников)
🔥 Видео

Видео:Цилиндр, конус, шар, 6 классСкачать

Чертежик

Метки

Видео:КАК НАРИСОВАТЬ ЦИЛИНДР ИЛИ КОНУС В ЛЮБОМ ПОЛОЖЕНИИ?/конструкция, тональность, эллипс.Скачать

Пересечение конуса и цилиндра пошаговое выполнение

Пересечение конуса и цилиндра имеют сопряжение осевых линий, поэтому вычерчивание осуществлено метод секущих сфер.

Ниже представлено задание на эту тему:

Читайте также: Как собрать главный тормозной цилиндр ваз 2106

Рассмотрим Пересечение конуса и цилиндра пошагово:

1.) Вычерчиваются фигуры в первоначальном виде согласно заданию.

2.) Строится первая секущая сфера с наименьшим радиусом (определяется по наибольшей ширине из двух фигур по углом 90 градусов)

3.) Окружность (имеет синий цвет) пересекла обе фигуры в двух точках. Необходимо соединить точки, тем самым образуются прямые, которые пересекаются в точках — это и есть необходимая точка для дальнейшего построения линии пересечения фигур.

4.) Чертится еще дополнительная окружность (обозначено сиреневым цветом), пересекающая конус в двух точках (их необходимо соединяют) и цилиндр в четырех точках (их тоже соединяют). В месте пересечения прямых конуса и цилиндра ставим точки.

Радиусы окружностей произвольные, кроме первоначального. Чем больше окружностей, тем точнее выглядит линия пересечения.

5.) Чертится дополнительная окружность (зеленым цветом), которая пересекает конус в двух точках и цилиндр. Точки соединяются и в месте сопряжения указывается необходимая точка.

6.) Следующим необходимо перенести точки в верхнем изображении в нижний. Для этого строится окружность в нижним изображении (синим цветом) и опускаются прямые до сопряжения с окружностью.

7.) Повторяется процесс перенос точек выполненный в 6 пункте, но теперь с сиреневым цветом.

8.) Повторяется процесс переноса точек описанный в 6 пункте (зеленым цветом).

9.) Переносятся последние точки, имеющие сопряжения в самых крайних точках сопряжения фигур: в верхней и нижней частях.

10.) Соединяются все точки плавной линией, образуя необходимую линию взаимно пересекающих фигур.

11.) Завершающим шагом является удаление всех дополнительных с последующей обводкой контуров соответствующими линиями чертежа.

Независимо от задания, получаемое от преподавателя, на выполнение подобного рода чертежа, то есть на пересечение конуса и цилиндра. Метод выполнения остается неизменным.

Видео:Построение конусаСкачать

Как начертить конус цилиндр

Видео:Цилиндр, вытянутый вдоль оси Z. Урок33.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Пошаговое решение задачи №9 — построение развертки конуса и цилиндра (Фролов / Бубенников)

Необходимо построить развертку поверхностей и перенести линию пересечения поверхностей на развертку. В основе данной задачи рассматриваются поверхности (конуса и цилиндра) с их линией пересечения, приведенные в предыдущей задаче 8.

Для решения таких задач по начертательной геометрии необходимо знать:

— порядок и методы построения разверток поверхностей;

— взаимное соответствие между поверхностью и ее разверткой;

— частные случаи построения разверток.

Порядок решения задачи

Читайте также: Прокладки под цилиндры буран

1. Отметим, что разверткой называется фигура, получаемая в
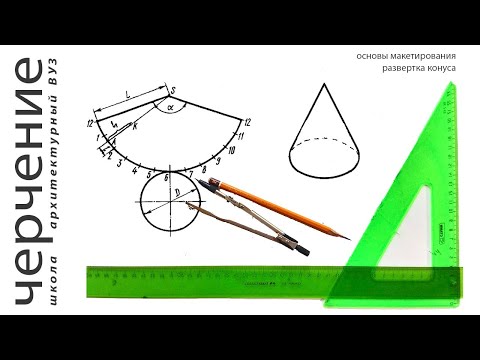
результате разреза поверхности по какой-либо образующей и постепенного разгибания ее до полного совмещения с плоскостью. Отсюда развертка, прямого кругового конуса — сектор с радиусом, равным длине образующей, и основанием, равным длине окружности основания конуса. Все развертки строятся только из натуральных величин.

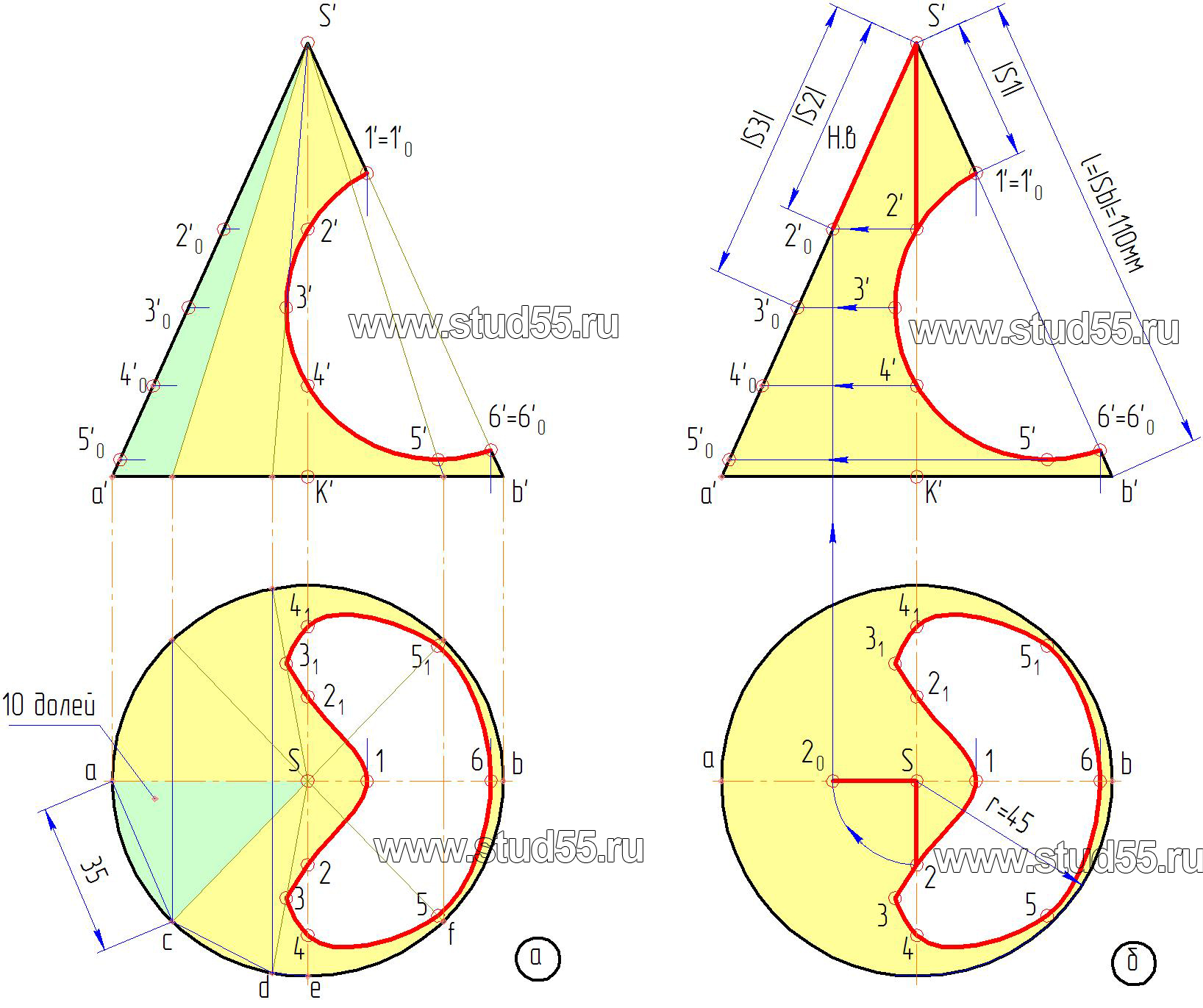
— длину окружности основания конуса, выраженную в натуральной величине делим на ряд долей: в нашем случае — 10, от количества долей зависит точность построения развертки (рис.9.1.а);

— откладываем полученные доли, заменяя их хордами, на длине
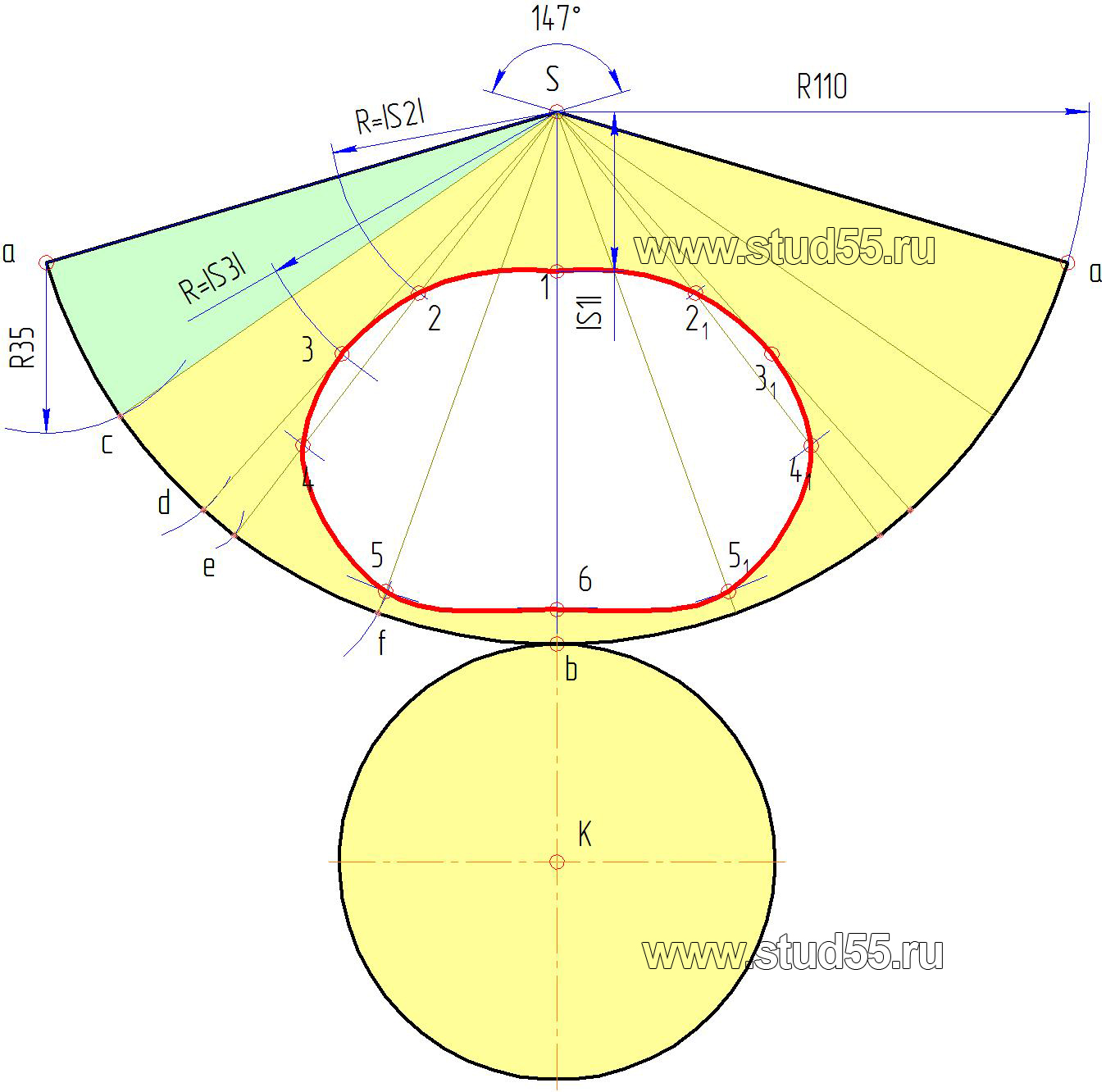
дуги, проведенной радиусом, равным длине образующей конуса l=|Sb|. Начало и конец отсчета долей соединяем с вершиной сектора — это и будет развертка боковой поверхности конуса.

Второй способ:

— строим сектор с радиусом, равным длине образующей конуса.
Заметим, что как в первом, так и во втором случае за радиус берется крайняя правая или левая образующие конуса l=|Sb|, т.к. они выражены в натуральной величине;

— при вершине сектора откладываем угол а, определяемый по формуле:

где r — величина радиуса основания конуса;

l — длина образующей конуса;

360 — постоянная переводная в градусы величина.

К сектору-развертке строим основание конуса радиуса r.

2. По условиям задачи требуется перенести линию пересечения
поверхностей конуса и цилиндра на развертку. Для этого используем свойства взаимной однозначности между поверхностью и ее разверткой, в частности, отметим, что каждой точке на поверхности соответствует точка на развертке и каждой линии на поверхности соответствует линия на развертке.

Отсюда вытекает последовательность перенесения точек и линий
с поверхности на развертку.

Для развертки конуса. Условимся, что разрез поверхности конуса произведен по образующей S’a’. Тогда точки 1, 2, 3,…6
будут лежать на окружностях (дугах на развертке) с радиусами соответственно равными величинам расстояний, взятым по образующей S’A’ от вершины S’ до соответствующей секущей плоскости с точками 1’, 2’, 3’…6’ -|S1|, |S2|, |S3|….|S6| (рис.9.1.б).

Положение точек на этих дугах определяется расстоянием, взятым с горизонтальной проекции от образующей Sa, по хорде до соответствующей точки, например до точки с, ас=35 мм (рис.9.1.а). Если расстояние по хорде и дуге сильно разнятся, то для уменьшения погрешности можно разделить большее количество долей и отложить их на соответствующие дуги развертки. Таким способом переносятся любые точки с поверхности на ее развертку. Полученные точки соединятся плавной кривой по лекалу (рис.9.3).

Читайте также: Загадка про цилиндр для дошкольников

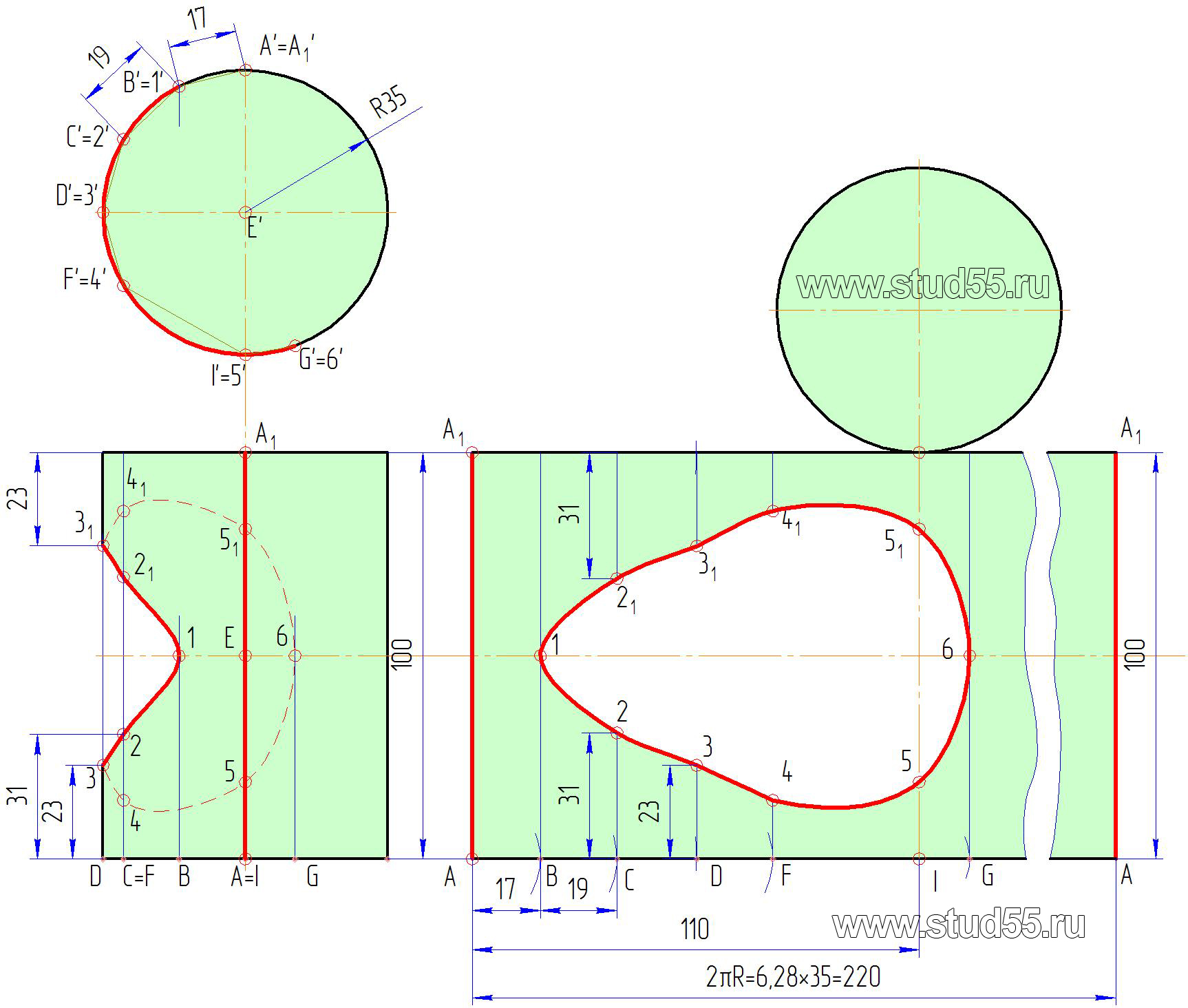
Для развертки цилиндра.

Развертка цилиндра есть прямоугольник с высотой, равной высоте образующей, и длиной, равной длине окружности основания цилиндра. Таким образом, для построения развертки прямого кругового цилиндра необходимо построить прямоугольник с высотой, равной высоте цилиндра, в нашем случае 100мм, и длиной, равной длине окружности основания цилиндра, определенной по известным формулам: C=2R=220мм, или делением окружности основания на ряд долей, как было указано выше. К верхней и нижней части полученной развертки пристраиваем основание цилиндра.

Условимся, что разрез произведен по образующей AA₁ (A’A’₁; AA1). Заметим, что разрез следует производить по характерным (опорным) точкам для более удобного построения. Учитывая, что длина развертки есть длина окружности основания цилиндра C, от точки A’=A’₁ разреза фронтальной проекции берем расстояние по хорде (если расстояние большое, то необходимо его разделить на доли) до точки B’ (в нашем примере — 17мм) и откладываем его на развертке (по длине основания цилиндра) от точки А. Из полученной точки В проводим перпендикуляр (образующую цилиндра). Точка 1 должна находиться на этом перпендикуляре) на расстоянии от основания, взятого с горизонтальной проекции до точки. В нашем случае точка 1 лежит на оси симметрии развертки на расстоянии 100/2=50мм (рис.9.4).

И так поступаем для нахождения на развертке всех других точек.

Подчеркнем, что расстояние по длине развертки для определения положения точек берется с фронтальной проекции, а расстояние по высоте — с горизонтальной, что соответствует их натуральным величинам. Полученные точки соединяем плавной кривой по лекалу (рис.9.4).

В вариантах задач, когда линия пересечения распадается на несколько ветвей, что соответствует полному пересечению поверхностей, способы построения (перенесения) линии пересечения на развертку аналогичны, описанным выше.