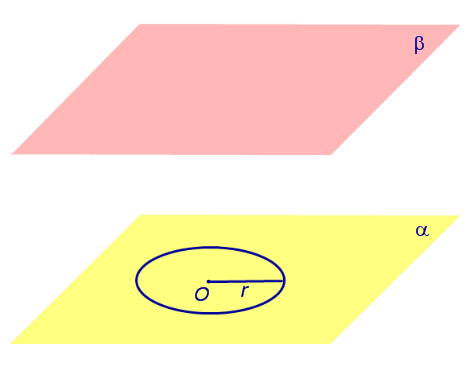
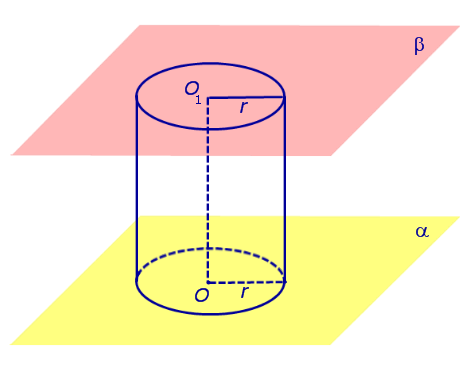
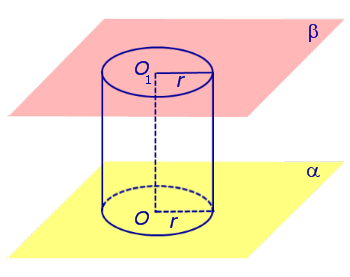
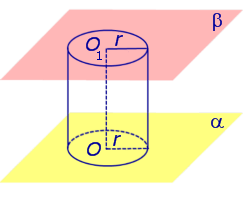
Как начертить цилиндр в стереометрии (8 видео)

Если из каждой точки окружности опустить перпендикуляр на плоскость β , то основания этих перпендикуляров образуют на плоскости β окружность радиуса r , центр O₁ которой является основанием перпендикуляра, опущенного из точки O на плоскость β (рис.2).

Отрезок перпендикуляра, опущенного из любой точки окружности с центром O на плоскость β , который заключен между плоскостями α и β , называют образующей цилиндра .

Совокупность всех образующих цилиндра называют цилиндрической поверхностью .

Фигуру, ограниченную цилиндрической поверхностью и плоскостями α и β, называют цилиндром .

Отрезок OO₁ называют осью цилиндра .

Радиус окружности Радиус окружности на плоскости α с центром в точке O называют радиусом цилиндра .

Круги с центрами O и O₁ на плоскостях α и β , называют основаниями цилиндра .

Замечание 1. Цилиндрическую поверхность часто называют боковой поверхностью цилиндра . Боковая поверхность цилиндра и основания цилиндра вместе составляют полную поверхность цилиндра .

Замечание 2. Каждая образующая цилиндра параллельна оси цилиндра, а длина каждой образующей цилиндра равна высоте цилиндра.

Замечание 3. Прямая OO₁ является осью симметрии цилиндра, а середина отрезка OO₁ является центром симметрии цилиндра.

Содержание

Сечения цилиндра
Объем цилиндра. Площадь боковой поверхности цилиндра. Площадь полной поверхности цилиндра
Как построить чертеж в стереометрической задаче
📽️ Видео

Видео:Цилиндр, вытянутый вдоль оси Z. Урок33.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать

Сечения цилиндра

Определение 2. Сечением цилиндра называют пересечение цилиндра с плоскостью.
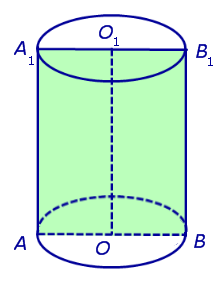
Если сечение проходит через ось цилиндра, то такое сечение называют осевым сечением цилиндра (рис. 3).

На рисунке 3 изображено одно из осевых сечений цилиндра – прямоугольник AA₁B₁B .

Замечание 4. Каждое осевое сечение цилиндра с радиусом r и высотой h является прямоугольником со сторонами 2r и h .

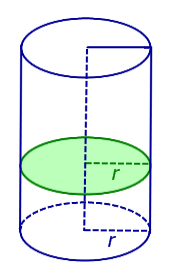
Определение 3. Перпендикулярным сечением цилиндра называют сечение, перпендикулярное оси цилиндра (рис. 4).

Замечание 5. Любым перпендикулярным сечением цилиндра будет круг радиуса r .

Замечание 6. Более подробно случаи взаимного расположения цилиндра и плоскости рассматриваются в разделе нашего справочника «Взаимное расположение цилиндра и плоскости в пространстве».

Видео:Как начертить цилиндр в объемеСкачать

Объем цилиндра. Площадь боковой поверхности цилиндра.
Площадь полной поверхности цилиндра

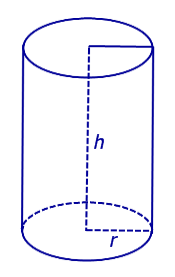
Для цилиндра с радиусом r и высотой h (рис. 5)

введем следующие обозначения

V	объем цилиндра
S_бок	площадь боковой поверхности цилиндра
S_полн	площадь полной поверхности цилиндра
S_осн	площадь основания цилиндра

Читайте также: Ваз главный тормозной цилиндр разборка сборка

Тогда справедливы следующие формулы для вычисления объема, площади боковой и полной поверхности цилиндра:

при помощи предельного перехода, когда число сторон правильной призмы n неограниченно возрастает. Однако доказательство этого факта выходит за рамки школьной программы.

Видео:Видеоурок по математике "Цилиндр"Скачать

Как построить чертеж в стереометрической задаче

При построении чертежа в стереометрической задаче мы изображаем объемную фигуру с помощью плоского чертежа. Мы это делаем с помощью параллельного проектирования.

Если вы знаете, что такое театр теней, то легко поймете, что такое параллельное проектирование.

В театре теней на объемную фигуру направляется свет, и в результате на экране (то есть на плоскости) появляется плоское изображение. Может получиться так:

Или так:

А если говорить о стереометрических фигурах, то так (представьте, что на каркас пирамиды справа направляется свет):

Остановимся на этом рисунке подробнее и дадим определение параллельной проекции точки на плоскость. Вектора , , и коллинеарны и задают направление проектирования.

Проведем через вершины пирамиды прямые, параллельные этим векторам. Точки пересечения этих прямых с плоскостью являются проекциями соответствующих точек пирамиды на плоскость :

Точка — проекция точки ;

точка — проекция точки ;

точка — проекция точки

и точка — проекция точки

Форма плоской фигуры, которую мы получаем при проектировании объемной зависит от направления проектирования и от расположения объемной фигуры. Но мы не можем из чего угодно получить что угодно. Параллельное проектирование подчиняется определенным правилам.

1. Параллельной проекцией прямой или отрезка будет прямая или отрезок.

2. Параллельные проекции параллельных отрезков либо параллельны друг другу, либо лежат на одной прямой.

3. Если точка делит отрезок в данном отношении, то проекция точки будет делить проекцию отрезка в том же отношении.

То есть при параллельном проектирование сохраняется параллельность и пропорциональность отрезков.

Когда мы делаем чертеж стереометрической фигуры, мы делаем чертеж ее параллельной проекции. При этом ребра объемной фигуры, которые невидимы, мы изображаем пунктирными линиями. На рисунке выше мы видим изображение проекции каркаса треугольной пирамиды . Ребро пирамиды невидимо для нас. Соответственно, ребро проекции мы изображаем пунктирной линией.

Читайте также: Маленькая компрессия в третьем цилиндре

Внимание! При параллельном проектирование не сохраняются ни углы, ни длины отрезков, ни отношения длин неколлинеарных отрезков (то есть отрезков, которые не лежат на параллельных прямых, или на одной прямой). Поэтому глядя на изображение проекции мы не можем определить соотношение отрезков и углов.

При изображении стандартных геометрических тел на плоскости нужно следить за тем, чтобы ребра и диагонали были все видны и не накладывались друг на друга.

В общем случае удобно строить в такой последовательности.

1. Начинаем с основания фигуры.

Если в основании треугольник, то вне зависимости от вида треугольника рисуем тупоугольный не равнобедренный треугольник, например, такой:

Если в основании прямоугольник или параллелограмм, то чертим параллелограмм. Удобно, чтобы величина острого угла на чертеже была около , в этом случае диагональ не наложится на сторону основания:

Если в основании трапеция, то чертим не равнобедренную трапецию. Тоже стараемся острый угол сделать поострее:

Если в основании круг, то чертим эллипс:

Если в основании правильный шестиугольник, то чертим проекцию правильного шестиугольника. Следим за тем, чтобы противоположные стороны шестиугольника были параллельны. Построение проекции правильного шестиугольника, как правило, вызывает наибольшие трудности. Поэтому если в вашем распоряжении есть листок в клеточку, то удобно строить по такому образцу:

2. Далее, если нужно построить прямую призму или прямой цилиндр, то из всех вершин основания проводим равные между собой вертикальные отрезки — это боковые ребра призмы или образующие цилиндра. В случае построения куба боковое ребро равно длине большей стороны параллелограмма, который изображен в основании:

3. Соединяем концы вертикальных отрезков и получаем верхнее основание:

4. Невидимые ребра изображаем пунктирными линиями:

В случае наклонной призмы или наклонного цилиндра боковые ребра изображаются параллельными отрезками:

5. При построении пирамиды или конуса сначала находим примерное расположение проекции вершины на плоскость основания. В треугольнике это может быть точка пересечения медиан, в прямоугольнике или шестиугольнике — точка пересечения диагоналей: