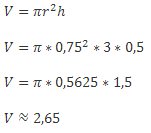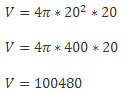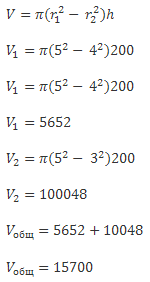Как находить объем части цилиндра

Объем цилиндра, формулы и калькулятор для вычисления объема цилиндра и площади его поверхностей, а также необходимая теория о характеристиках цилиндра.

Видео:Найдите объем V части цилиндра, изображенной на рисунке.Скачать

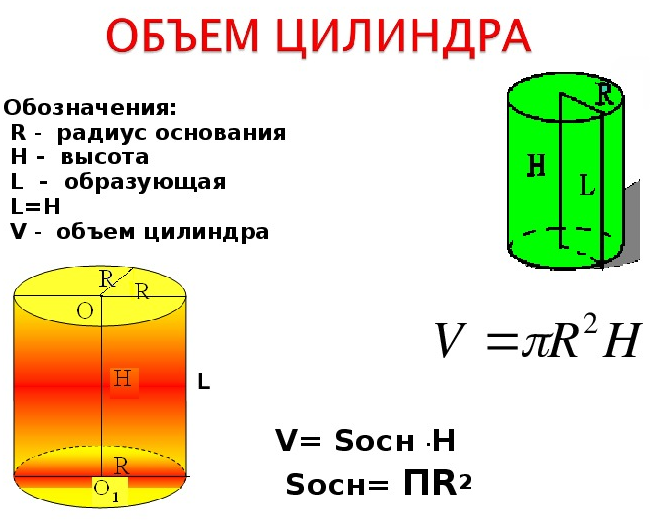
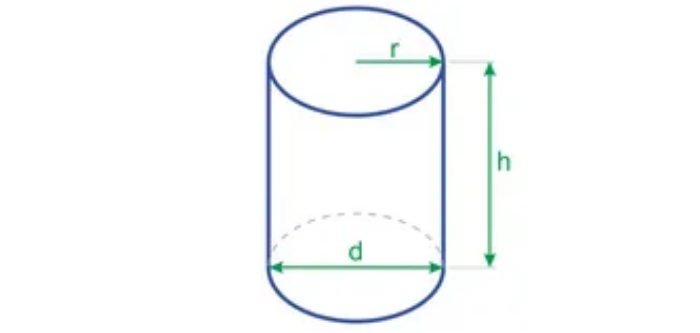
Объем правильного цилиндра через радиус и высоту цилиндра

Видео:Найдите объем V части цилиндра, изображенной на рисунке.Скачать

Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра

Видео:Найдите объем V части цилиндра, изображенной на рисунке.Скачать

Формулы и калькулятор для вычисления объема цилиндра через диаметр основания

Видео:Найдите объем V части цилиндра, изображенной на рисунке.Скачать

Объем цилиндрической полости

Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.

На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.

Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.

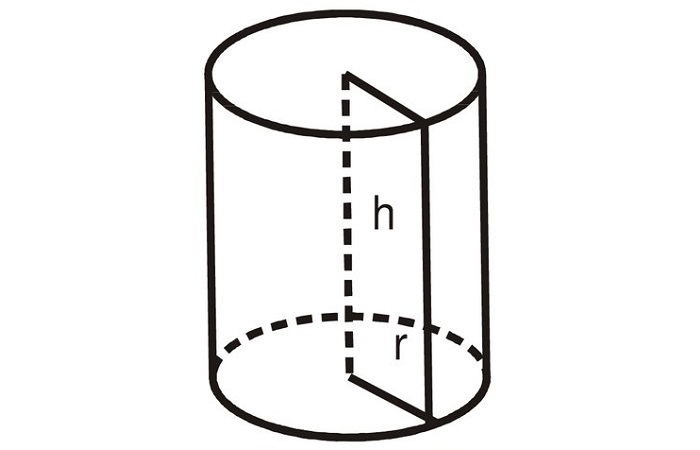
Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.

Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.

Рассмотрим правильный цилиндр.

Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник

Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра.

Радиус основания цилиндра, является радиусом цилиндра.

Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.

Читайте также: Пробка блока цилиндров заз шанс

Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.

Видео:Видеоурок по математике "Цилиндр"Скачать

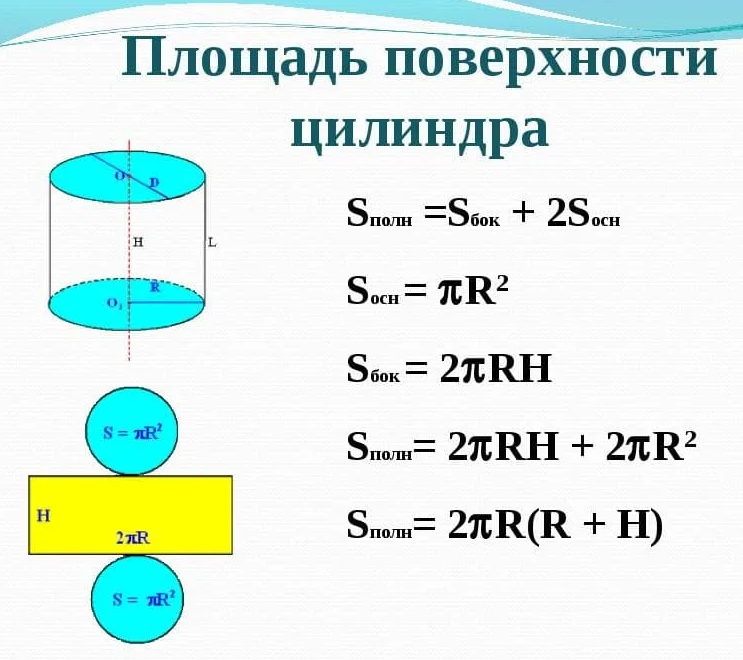
Поверхности цилиндра

Наружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая.

Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой.

Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке).

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

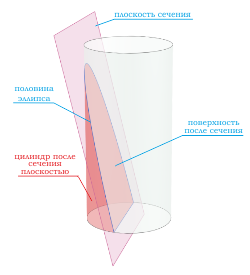
Сечения цилиндра

При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура .

При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник , но две боковые стороны которого будут являться кривыми линиями.

Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг .

Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс .

Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса .

Видео:Объём цилиндраСкачать

Что такое объем

Объем тела (геометрической фигуры) – это количественная характеристика, характеризующая количество пространства, занимаемого телом. Объем выражается в кубических единицах измерения, например: мм 3 , см 3 , мл 3 .

Формула вычисления объема цилиндра часто применяются при расчете массы различных цилиндров, например, прутков, заготовок и т.п. Для вычисления массы, необходимо вычисленный объем цилиндра умножить на плотность материала из которого цилиндр.

Так же, вычислить объём цилиндра иногда требуется для определения полости в виде цилиндра (цилиндрическая полость). В данном случае объём полости будет равен объёму цилиндра, который полностью занимает эту полость.

Объем и площадь других видов цилиндров рассмотрен в статьях:

Видео:Стереометрия на ЕГЭ по математике. Вычисление объема части цилиндра.Скачать

Объём части цилиндра

Объём части цилиндра. Здравствуйте, друзья! Для вас ещё одна статья с задачами про объём цилиндра. На момент написания этих строк данная группа задач исключена из открытого банка заданий ЕГЭ по математике, но они всегда туда могут «вернуться», и разумеется, их присутствие в составе заданий на самом экзамене вполне возможно. Это задачи на вычисление объёма части цилиндра. Задачки простенькие, решаются в 1-2 действия. Посмотрите, объём каких тел требуется найти:

*В условии задаются радиус основания, высота и угол сектора.

Читайте также: Тормозной цилиндр передний правый ваз 2110 артикул

Если вы ещё не изучили статью, где речь шла об объёме части конуса, то посмотрите обязательно , здесь принцип решения тот же. Повторять его не буду. Напомню только формулу объёма цилиндра:

*Ещё можете посмотреть статью , в которой мы уже разобрали несколько заданий, связанных с объёмом цилиндра.

Также есть следующие формы тел, объём которых требуется найти, вот эскизы:

Рисунок Б. Тело состоит из цилиндра, на который как бы сверху поставили ещё полцилиндра. То есть чтобы найти объём такого тела, необходимо вычислить объёмы двух этих отдельных тел (цилиндра и полуцилиндра) и суммировать их.

Рисунок В. Тело представляет собой цилиндр, из которого как бы «вырезан» другой цилиндр. Для вычисления объёма тела достаточно найти объём «полного» цилиндра и затем из него вычесть объём пустого пространства (он тоже имеет форму цилиндра и объём вычисляется без труда). Рассмотрим задачи:

25739. Найдите объем V части цилиндра, изображённой на рисунке. В ответе укажите V/Пи.

Часть цилиндра построенного на секторе круга с углом в 90 0 составляет четвёртую часть от полного объёма:

Результат делим на Пи и записываем ответ.

25743. Най­ди­те объем V части ци­лин­дра, изоб­ра­жен­ной на ри­сун­ке. В от­ве­те ука­жи­те V/Пи.

Часть цилиндра построенного на секторе круга с углом в 270 0 (из трёхсот шестидесяти мы вычли девяносто) составляет три четвёртых от полного объёма:

Результат делим на Пи и записываем ответ.

27199. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/Пи.

Часть цилиндра построенного на секторе круга с углом в 300 0 (из трёхсот шестидесяти мы вычли шестьдесят) составляет:

от полного объёма. Таким образом

Результат делим на Пи и записываем ответ.

25755. Най­ди­те объем V части ци­лин­дра, изоб­ра­жен­ной на ри­сун­ке. В от­ве­те ука­жи­те V/Пи.

Часть цилиндра построенного на секторе круга с углом в 60 0 составляет:

от полного объёма. Таким образом

Результат делим на Пи и записываем ответ.

25779. Най­ди­те объем V части ци­лин­дра, изоб­ра­жен­ной на ри­сун­ке. В от­ве­те ука­жи­те V/Пи.

Вычисляем объём цилиндра с радиусом равным 4 и высотой равной 3:

Вычисляем объём половины цилиндра с радиусом 4 и высотой равной 4 – 3 = 1

Результат делим на Пи и записываем ответ.

25781. Най­ди­те объем V части ци­лин­дра, изоб­ра­жен­ной на ри­сун­ке. В от­ве­те ука­жи­те V/Пи.

Вычисляем объём цилиндра с радиусом равным 4 и высотой 5:

Вычисляем объём «вырезанного» цилиндра (пустой части) с радиусом 2 и высотой 5:

Результат делим на Пи и записываем ответ.

Читайте также: Схема установки рабочего цилиндра сцепления

27196. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/Пи.

27197. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/Пи.

27198. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/Пи.

27200. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/Пи.

27201. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/Пи.

Видео:11 класс. Геометрия. Объем цилиндраСкачать

Объем цилиндра — формулы и примеры расчетов

Как найти объем цилиндра? Любой грамотный человек обязан отличить радиус от диаметра, знать, что такое высота, помнить основные формулы геометрии и уметь рассчитать объем шара или куба.

Практическое использование геометрических формул в повседневной жизни очень высоко. Рассчитать объем в кубических метрах перевозимого груза транспортной компанией, пропускную способность трубы под домом и многое другое — во всех этих и подобных им случаях поможет геометрия.

Видео:11 класс, 32 урок, Объем цилиндраСкачать

Как найти объем цилиндра

При упоминании о цилиндре на ум приходит классический головной убор. Кроме него в окружении можно встретить много разновидностей этой фигуры.

В теории — это тело, которое ограничено цилиндрической поверхностью и пересекающими её параллельными плоскостями.

Рассчитать его объем возможно следующим образом:

Как видите, формула проста и прозрачна, и если обывателю нужно, как вариант, определить объем цистерны воды, можно смело ее использовать. Хотя, если возникают сомнения в правильности расчетов, для этой цели можно использовать калькулятор и определить объем онлайн.

Видео:Объем цилиндраСкачать

Формула объема цилиндра через диаметр

К сожалению, случается, что при расчете объема фигуры известны не все размеры. Так, например, может не быть данных о радиусе.

В данном случае, если знать диаметр или иметь возможность его измерить, можно воспользоваться следующей формулой:

Видео:Объём цилиндраСкачать

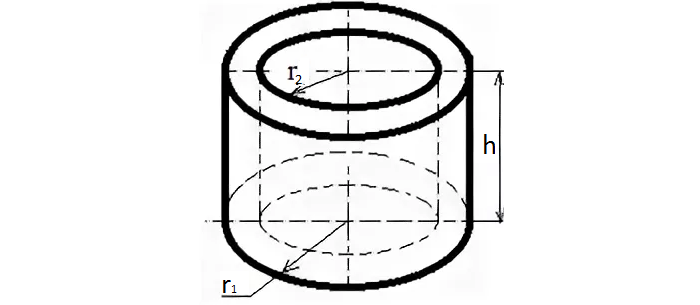
Объем полого цилиндра

Расчет полого цилиндра нужен, когда необходимо, например, рассчитать вес полой трубы. Ее масса равна произведению плотности материала и объема.

Видео:Объем части цилиндраСкачать

Примеры задач с решениями

Задача №1

Высота бочки с водой равна 3 метрам, радиус составляет 0,75 метра. Рассчитать в литрах, сколько нужно жидкости, чтобы заполнить емкость наполовину?

Задача №2

В цехе подготовили заготовку цилиндра. Диаметр основания равен высоте и составляет 20 см. Нужно найти объем заготовки.

Задача №3

На производстве нужно изготовить две трубы с двумя равными поверхностями. Внешний радиус первой трубы равен 5см, а внутренний 4 см, высота 200 см. Внутренний радиус второй равен 3 см.

Сколько понадобится материала для изготовления труб?

🔥 Видео

ЕГЭ СТЕРЕОМЕТРИЯ НАХОЖДЕНИЯ ОБЪЕМА ЧАСТИ ЦИЛИНДРА | ЭКСКЛЮЗИВНАЯ ЗАДАЧА НА ОБЪЕМ ФИГУРЫ | ГАРМАШУКСкачать

60. Площадь поверхности цилиндраСкачать

ЕГЭ математика 8#8🔴Скачать

Задача про ЦИЛИНДР / Как найти объем детали? / Профиль ЕГЭСкачать

Найдите объем V части цилиндра, изображенной на рисункеСкачать

11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Объем цилиндра. Практическая часть. 11 класс.Скачать