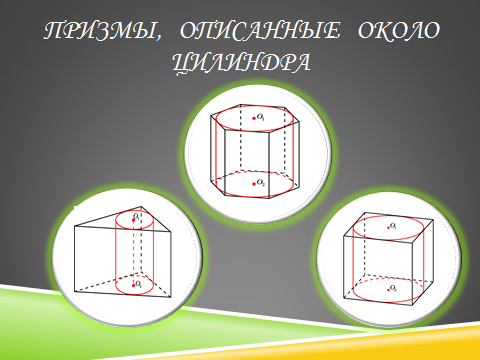
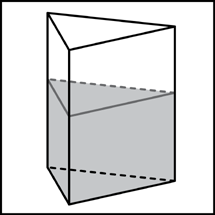
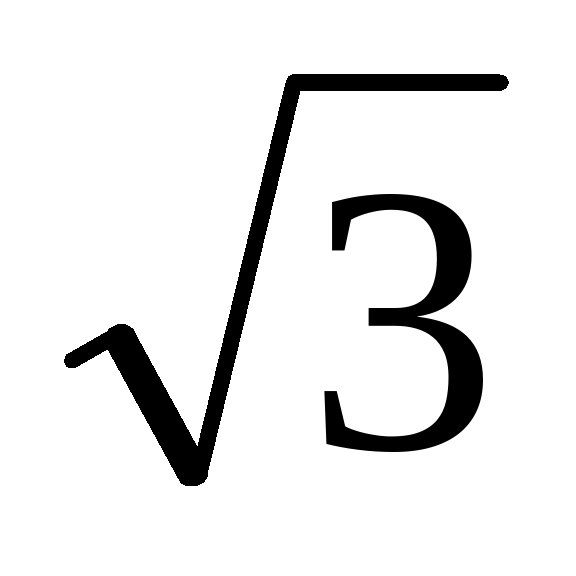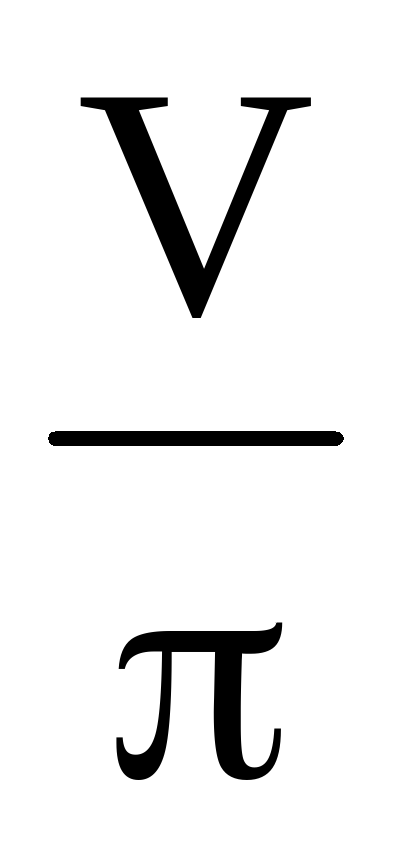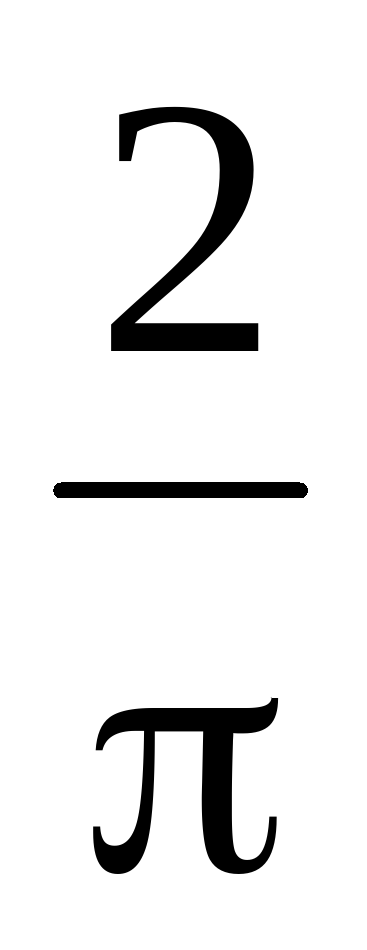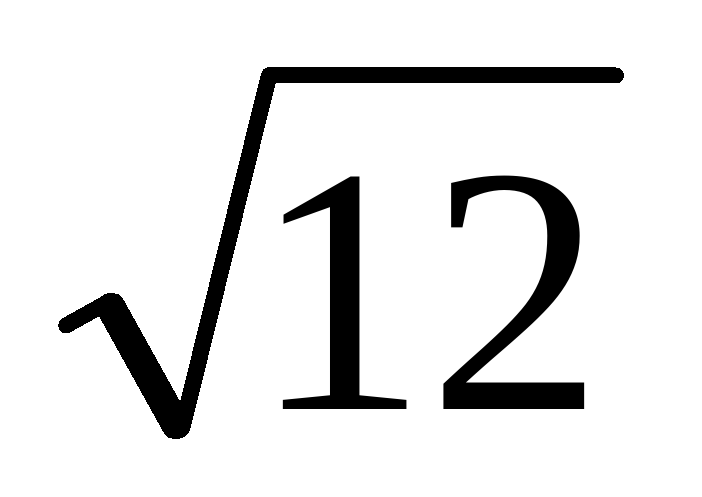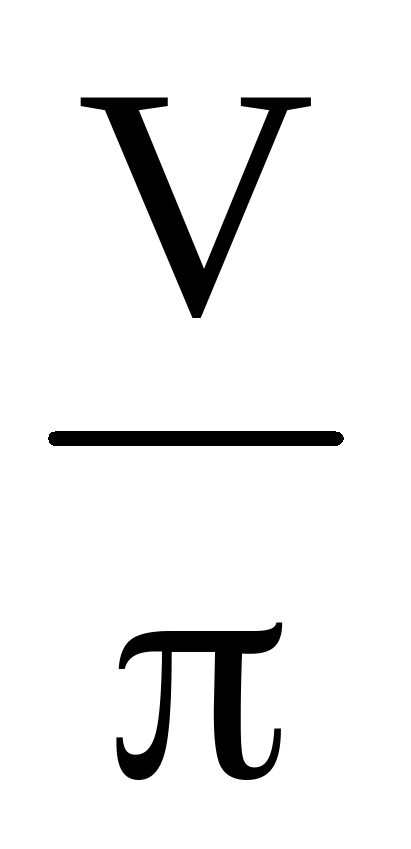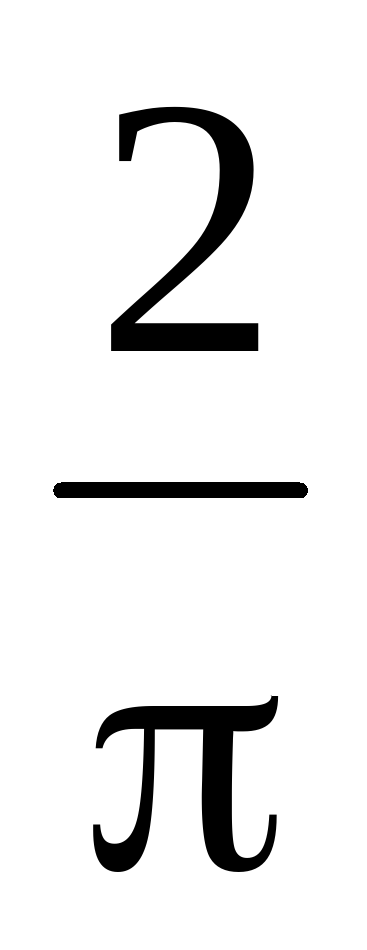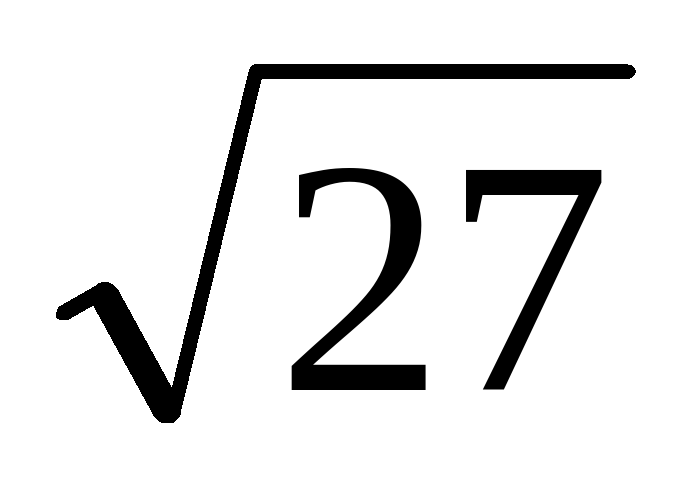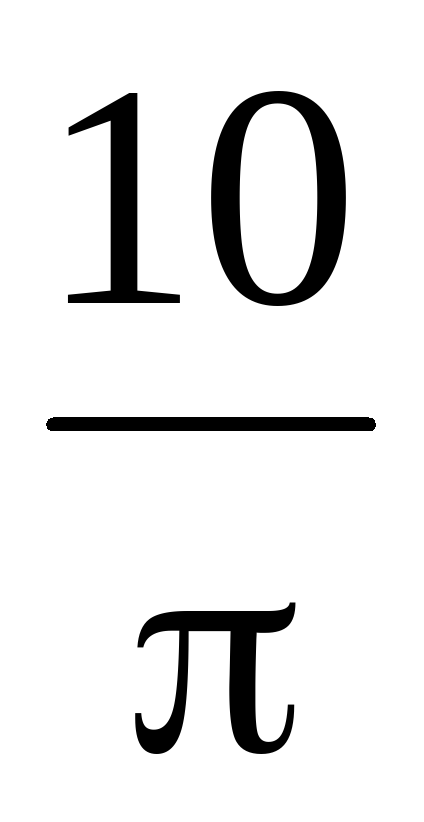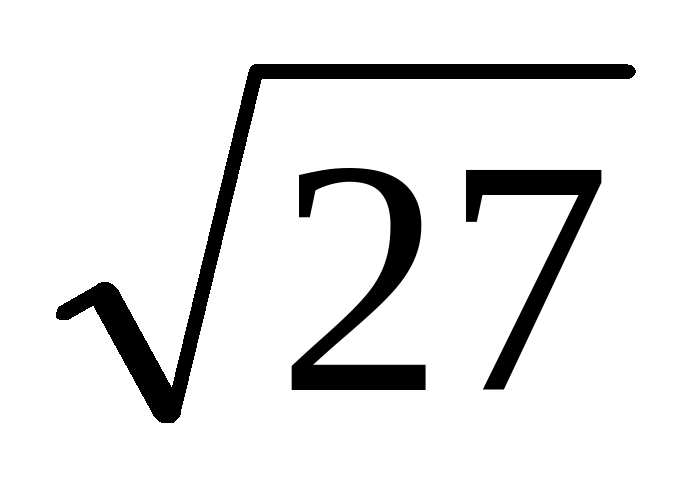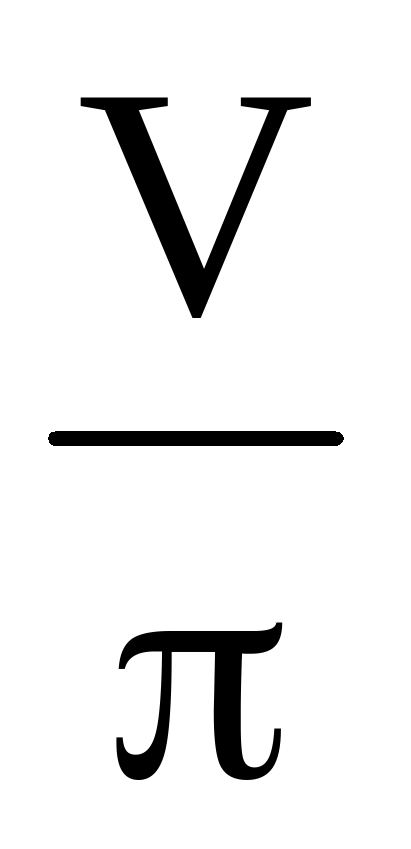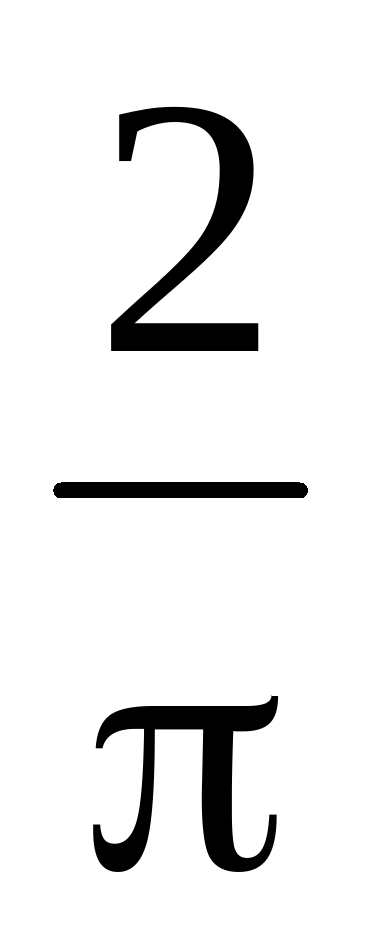- Цилиндры, вписанные в призмы. Свойства призмы, описанной около цилиндра
- Отношение объемов цилиндра и описанной около него правильной n — угольной призмы
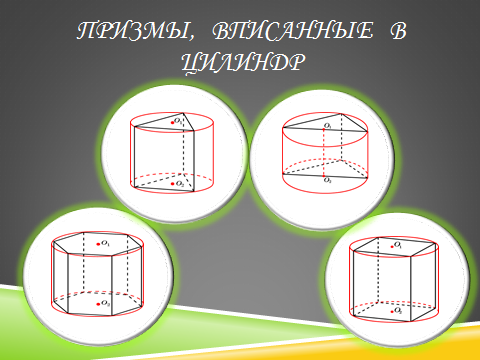
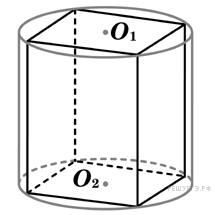
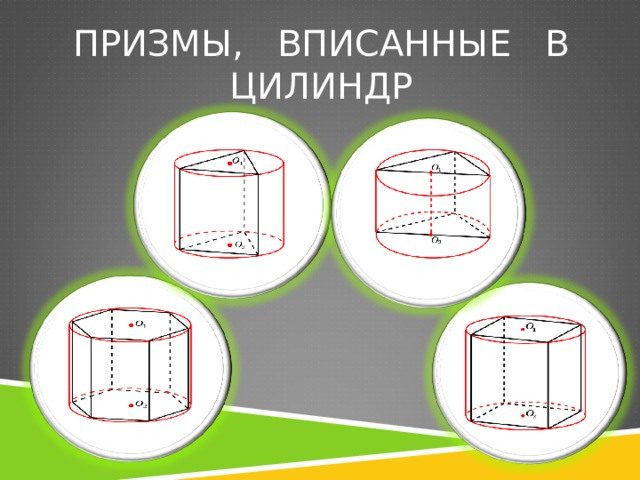
- Призмы, вписанные в цилиндры
- Призмы, вписанные в цилиндр. Свойства призмы, вписанной в цилиндр
- Как находить объем цилиндра описанного около призмы
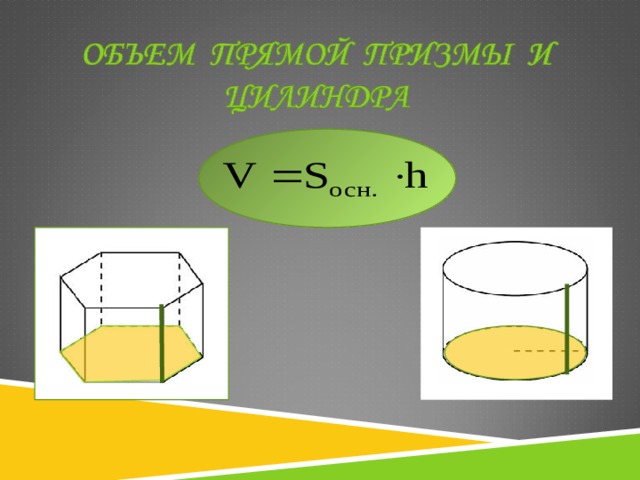
- «Объем прямой призмы и цилиндра»
- Просмотр содержимого документа «Объем прямой призмы и цилиндра»
- Просмотр содержимого документа «Приложение 1»
- Просмотр содержимого документа «Приложение 2»
- Просмотр содержимого документа «Приложение 3»
- Просмотр содержимого документа «Приложение 4»
- Просмотр содержимого презентации «Презентация»
- Просмотр содержимого презентации «Приложение 5»
- 📺 Видео
Видео:Геометрия Цилиндр описан около шара. Найдите объем шара, если известно, что объем цилиндра равен 60.Скачать

Цилиндры, вписанные в призмы. Свойства призмы, описанной около цилиндра
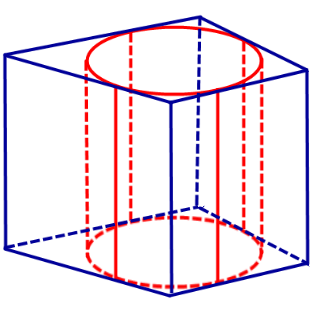
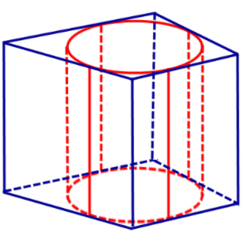
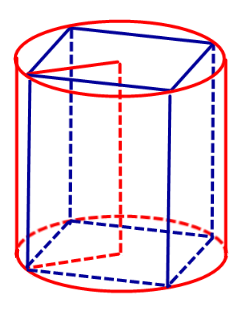
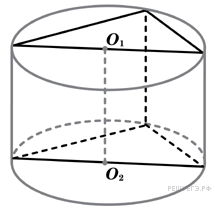
Определение 2. Если цилиндр вписан в призму, то призму называют описанной около цилиндра.
Прежде, чем перейти к вопросу о том, в какую же призму можно вписать цилиндр, докажем следующее свойство призм.
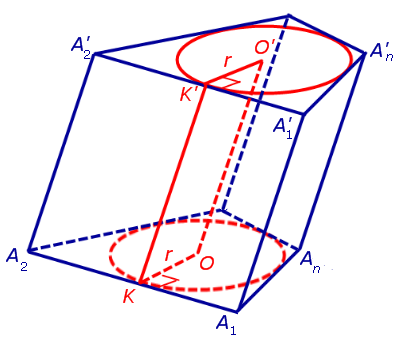
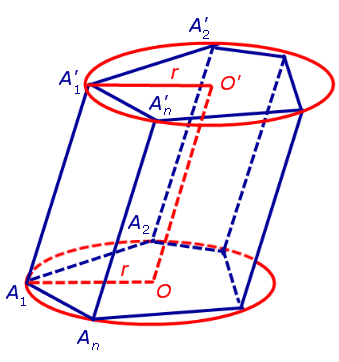
Утверждение 1. Если в основания призмы можно вписать окружности, то отрезок, соединяющий центры вписанных окружностей, будет параллелелен и равен боковому ребру призмы.
Рассуждая аналогичным образом, заключаем, что точка O’ равноудалена от всех прямых, на которых лежат ребра верхнего основания A’1A’2, A’2A’3, . , An – 1An , а поскольку O’ лежит в плоскости верхнего основания, то точка O’ является центром вписанной в многоугольник A’1A’2 . A’n окружности.
В силу того, что прямые OO’ и A1A’1 параллельны по построению, а прямые OA1 и O’A’ параллельны как линии пересечения двух параллельных плоскостей третьей плоскостью, замечаем, что четырехугольник OO’A1A’1 является параллелограммом, откуда вытекает равенство: OO’ = A1A’1 .
Теорема. В призму можно вписать цилиндр тогда и только тогда, когда выполнены следующие два условия:
- Призма является прямой призмой;
- В основания призмы можно вписать окружности.
Доказательство. Докажем сначала, что если в n – угольную призму вписан цилиндр, то оба условия теоремы выполнены.
Действительно, выполнение условия 2 следует непосредственно из определения цилиндра, вписанного в призму. Докажем, что выполняется и условие 1, т.е. докажем, что описанная около цилиндра призма является прямой призмой.
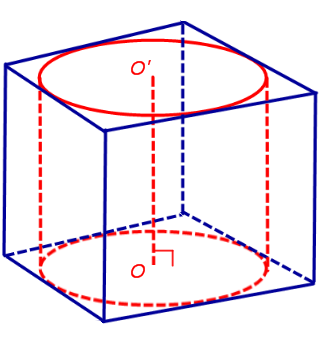
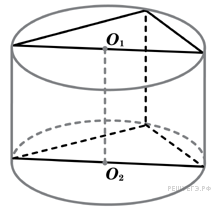
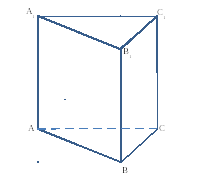
С этой целью рассмотрим ось цилиндра OO’ , соединяющую центры окружностей, вписанных в нижнее и верхнее основания призмы (рис. 3).
Согласно утверждению 1 отрезок OO’ параллелен боковым ребрам призмы. Поскольку ось цилиндра OO’ перпендикулярна к плоскостям его оснований, то и боковые ребра призмы также перпендикулярны к плоскостям оснований, то есть призма является прямой призмой.
Таким образом, мы доказали, что, если призма описана около цилиндра, то оба условия теоремы выполнены.
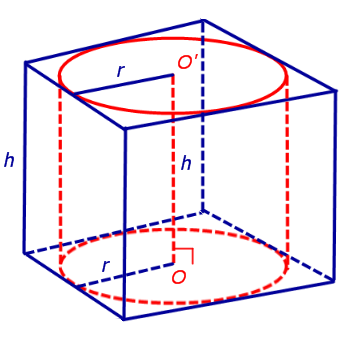
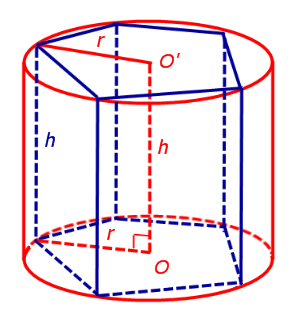
Теперь рассмотрим прямую n – угольную призму высоты h, в основания которой можно вписать окружности, и докажем, что в такую призму можно вписать цилиндр.
Обозначим буквой O центр окружности радиуса r, вписанной в нижнее основание призмы, а символом O’ обозначим центр окружности, вписанной в верхнее основание призмы (рис. 4).
Поскольку многоугольники, лежащие в основаниях призмы равны, то и радиусы вписанных в них окружностей будут равны. Согласно утверждению 1 отрезок OO’ параллелен и равен боковому ребру призмы. Так как рассматриваемая призма прямая, то ее боковые ребра перпендикулярны плоскости основания и равны высоте призмы h. Значит, и отрезок OO’ перпендикулярен плоскости основания призмы и равен h.
Цилиндр с осью OO’ , радиусом r и высотой h и будет вписан в исходную призму.
Доказательство теоремы завершено.
Следствие 1 . Высота призмы, описанной около цилиндра, равна высоте цилиндра.
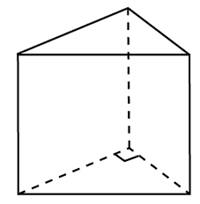
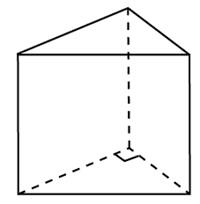
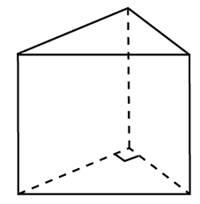
Следствие 2. В любую прямую треугольную призму можно вписать цилиндр.
Справедливость этого утверждения вытекает из того факта, что в любой треугольник можно вписать окружность.
Следствие 3. В любую правильную n – угольную призму можно вписать цилиндр.
Для доказательства этого следствия достаточно заметить, правильная призма является прямой призмой. Основаниями правильной призмы являются правильные многоугольники, а в любой правильный n – угольник можно вписать окружность.
Видео:ЕГЭ математика СТЕРЕОМЕТРИЯ 8#5.18🔴Скачать

Отношение объемов цилиндра и описанной около него правильной n — угольной призмы
Задача. Найти отношение объемов цилиндра и описанной около него правильной n — угольной призмы.
Решение. Поскольку и объем цилиндра, и объем призмы объем призмы вычисляются по формуле
а высота цилиндра равна высоте описанной около него призмы, то для объемов цилиндра и описанной около него правильной n — угольной призмы справедливо равенство
Следствие 4. Отношение объема цилиндра к объему описанной около него правильной треугольной призмы правильной треугольной призмы равно
Следствие 5. Отношение объема цилиндра к объему описанной около него правильной четырехугольной призмы правильной четырехугольной призмы равно
Следствие 6. Отношение объема цилиндра к объему описанной около него правильной шестиугольной призмы равно
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

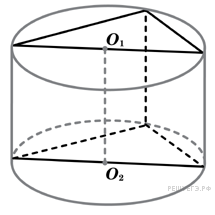
Призмы, вписанные в цилиндры
Видео:11 класс, 32 урок, Объем цилиндраСкачать

Призмы, вписанные в цилиндр. Свойства призмы, вписанной в цилиндр
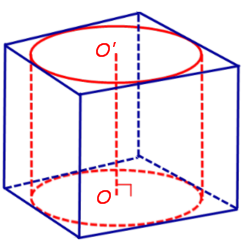
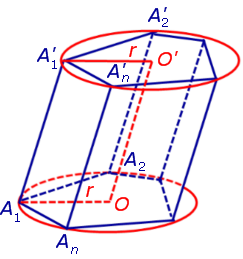
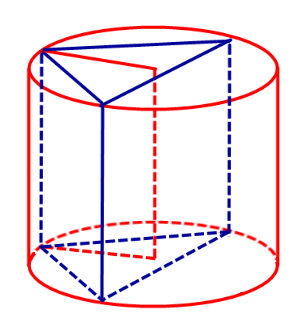
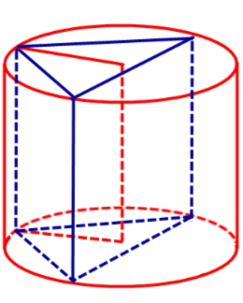
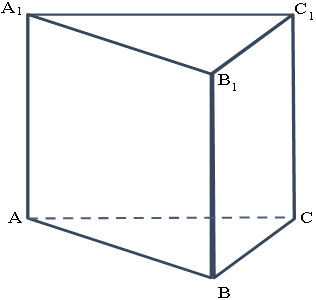
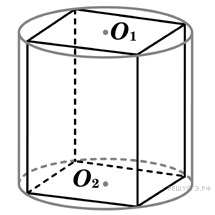
Определение 1. Призмой, вписанной в цилиндр, называют такую призму, основания которой вписаны в окружности оснований цилиндра, а боковые ребра призмы являются образующими цилиндра (рис. 1).
Определение 2. Если призма вписана в цилиндр, то цилиндр называют описанным около призмы.
Прежде, чем перейти к вопросу о том, какую призму можно вписать в цилиндр, докажем следующее свойство призм.
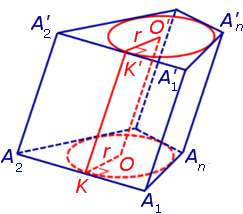
Утверждение 1. Если около оснований призмы можно описать окружности, то отрезок, соединяющий центры описанных окружностей, будет параллелелен и равен боковому ребру призмы.
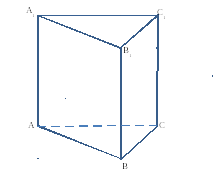
Докажем, что точка O’ является центром окружности радиуса r, описанной около верхнего основания призмы. С этой целью рассмотрим, например, четырехугольник A1A’1O’O (рис. 2).
Рассуждая аналогичным образом, заключаем, что
то есть точка O’ – центр окружности радиуса r , описанной около верхнего основания призмы.
В силу того, что четырехугольник OO’A1A’1 является параллелограммом, получаем равенство
Теорема. Около призмы можно описать цилиндр тогда и только тогда, когда выполнены следующие два условия:
- Призма является прямой призмой;
- Около оснований призмы можно описать окружности.
Доказательство. Докажем сначала, что если около n – угольной призмы описан цилиндр, то оба условия теоремы выполнены.
Действительно, выполнение условия 2 следует непосредственно из определения цилиндра, описанного около призмы. Из этого определения также следует, что вписанная в цилиндр призма является прямой призмой, поскольку образующие цилиндра перпендикулярны к плоскостям его оснований,
Таким образом, мы доказали, что, если призма вписана в цилиндр, то оба условия теоремы выполнены.
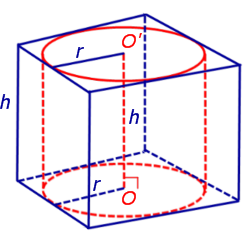
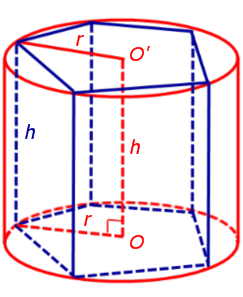
Теперь рассмотрим прямую n – угольную призму высоты h, около оснований которой можно описать окружности, и докажем, что около такой призмы можно описать цилиндр.
Обозначим буквой O центр окружности радиуса r, описанной около нижнего основания призмы, а символом O’ обозначим центр окружности, описанной около верхнего основания призмы.
Поскольку многоугольники, лежащие в основаниях призмы равны, то и радиусы описанных около них окружностей будут равны. Согласно утверждению 1 отрезок OO’ параллелен и равен боковому ребру призмы. Так как рассматриваемая призма прямая, то ее боковые ребра перпендикулярны плоскости основания и равны высоте призмы h. Значит, и отрезок OO’ перпендикулярен плоскости основания призмы и равен h.
Цилиндр с осью OO’ , радиусом r и высотой h и будет описан около исходной призмы.
Доказательство теоремы завершено.
Следствие 1. Высота призмы, вписанной в цилиндр, равна высоте цилиндра.
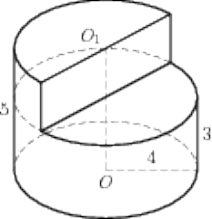
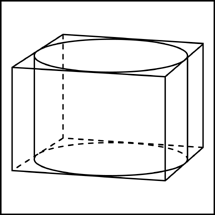
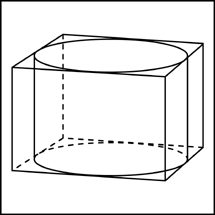
Следствие 2. Около любой прямой треугольной призмы можно описать цилиндр (рис. 4).
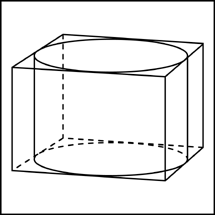
Следствие 3. Около любого прямоугольного параллелепипеда (в частности, около куба прямоугольного параллелепипеда (в частности, около куба ) можно описать цилиндр (рис. 5).
Замечание 1. Если у прямоугольного параллелепипеда прямоугольного параллелепипеда три ребра, выходящие из одной вершины, равны a, b, c и различны, то существует три возможности описать около этого параллелепипеда цилиндр в зависимости от того, какое из ребер параллелепипеда выбрано в качестве образующей описанного цилиндра (рис. 6, 7, 8).
Видео:Объём цилиндраСкачать

Как находить объем цилиндра описанного около призмы
Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.
Читайте также: Главный цилиндр сцепления luk 511017610
Радиусы шара и основания цилиндра равны. Площадь поверхности цилиндра, с радиусом основания r и высотой 2r равна
Площадь поверхности шара радиуса r равна то есть в 1,5 раза меньше площади поверхности цилиндра. Следовательно, площадь поверхности шара равна 12.
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому площадь основания равна 4, а объем параллелепипеда равен
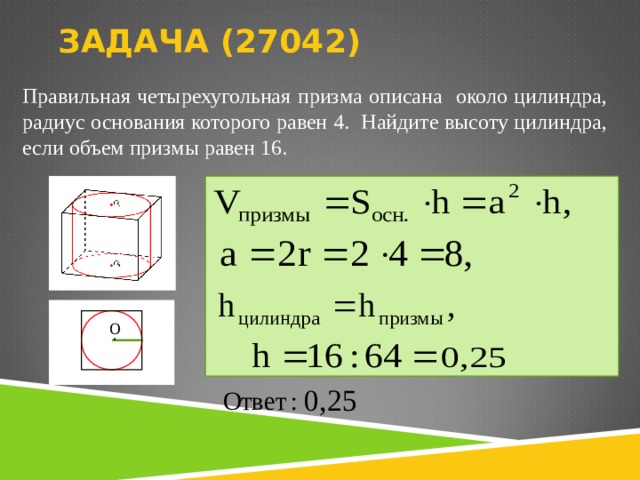
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.
Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому сторона основания равна 8, а площадь основания равна 64. Тогда высота цилиндра равна
Почему получилось 64? Что-то не понятно:(
Длина диаметра цилиндра равна длине стороны квадрата в основании.
В куб вписан шар радиуса 1. Найдите объем куба.
Ребро куба равно диаметру вписанного в него шара, а объем куба равен кубу его ребра. Отсюда имеем:
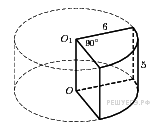
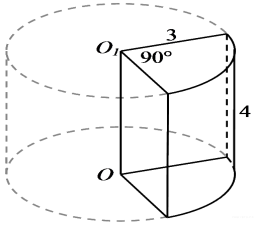
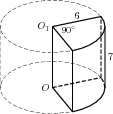
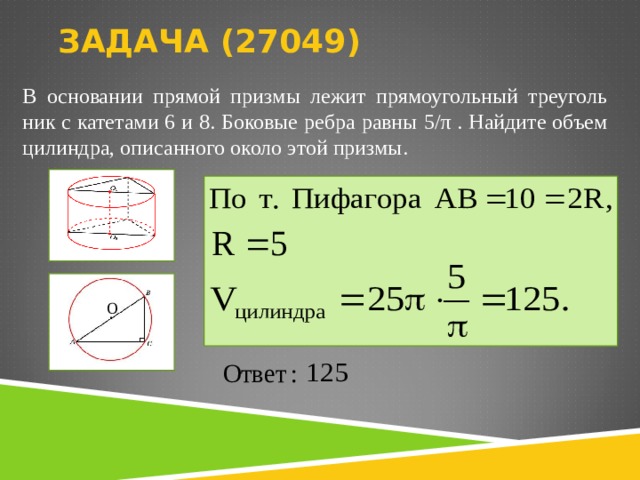
В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.
По теореме Пифагора длина гипотенузы треугольника в основании Поскольку гипотенуза является диаметром основания описанного цилиндра, его объем
Видео:07 Стереометрия на ЕГЭ по математике. Призма вписана в цилиндр.Скачать

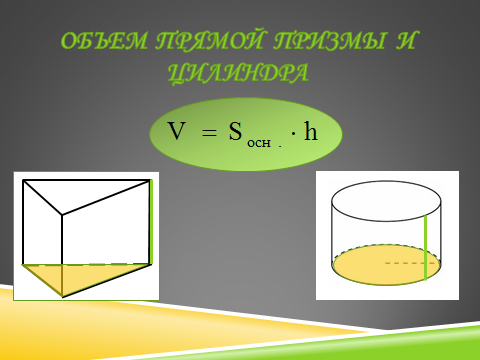
«Объем прямой призмы и цилиндра»
Просмотр содержимого документа
«Объем прямой призмы и цилиндра»
ПЛАН-КОНСПЕКТ УРОКА «Объем прямой призмы и цилиндра»
Школа: МОУ «Лицей №1», г. Воркуты.
Учитель: Курылева Светлана Сергеевна
Тема: Объемы прямой призмы и цилиндра (задача 8 в ЕГЭ).
Тип урока: урок обучения умениям и навыкам .
Форма урока : урок-практикум.
Цель на урок : выработать умение применять формулы для вычисления объёма прямой призмы и цилиндра при решении задач.
дидактические: повторить формулы для вычисления объема прямой призмы и цилиндра многоугольников; учиться применять формулы для вычисления объема прямой призмы и цилиндра при решении задач; рассмотреть задачи на вычисление объема призмы, вписанной в цилиндр и призмы, описанной около цилиндра; контроль уровня усвоения основных знаний, умений и навыков по данной теме.
развивающие: развивать познавательный интерес у учащихся, логическое мышление, интеллектуальные способности; формировать математическую речь; развивать умения применять знания в конкретной ситуации; развитие самостоятельной деятельности обучающихся.
воспитательные: воспитывать у учащихся потребность в приобретении и углублении знаний, вырабатывать умение слушать и вести диалог, формировать эстетические навыки при оформлении записей в тетради.
Оборудование: компьютер, мультимедийный проектор, экран, листы на каждого ученика с подбором заданий по теме урока, заданий для самостоятельной работы, домашней работы, дополнительная задача.
Средства обучения: мультимедийная презентация к уроку «Объем прямой призмы и цилиндра».
I . Организационный момент.
Сегодня на уроке мы будем решать задачи по теме «Объемы прямой призмы и цилиндра» из открытого банка ЕГЭ, это группы В10, В13.
Французский государственный и военный деятель, инженер и ученый Лазар Карно сказал: «Первое условие, которое надлежит выполнять в математике, – это быть точным, второе – быть ясным и, насколько можно, простым».
Исходя из темы урока, какие задачи вы можете перед собой поставить?
Задачи, которые мы сегодня будем разбирать, может быть, кому-то покажутся легкими, но без знания соответствующего теоретического материала справиться с ними практически нельзя.
На предыдущем уроке мы вывели формулы для вычисления объемов прямой призмы и цилиндра. Какова общая запись этих формул?
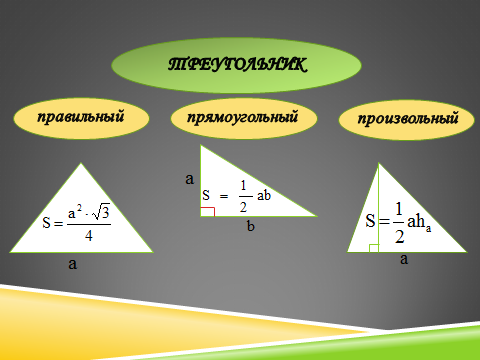
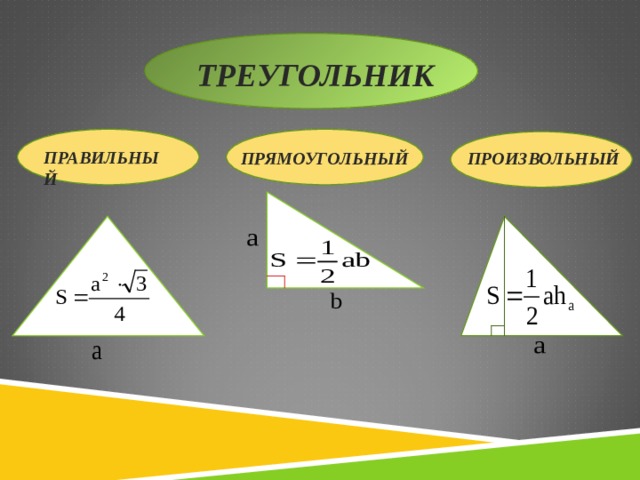
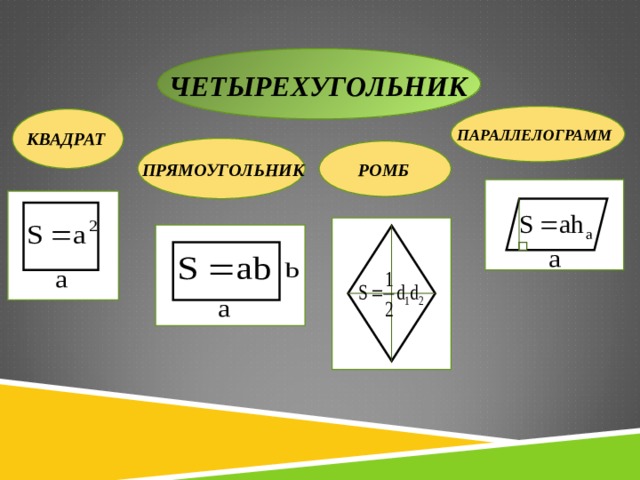
Какие фигуры наиболее часто встречаются в основании прямой призмы в задачах ЕГЭ?
Как найти площадь прямоугольного треугольника, правильного треугольника, произвольного треугольника? Какие еще формулы для вычисления площади произвольного треугольника вы знаете?
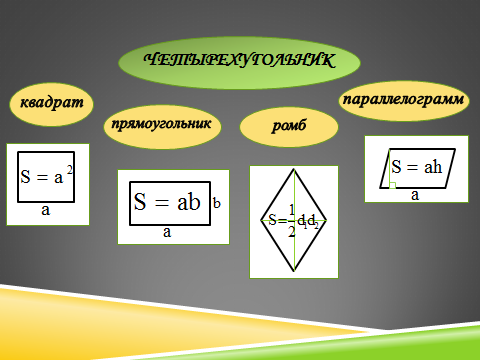
Как найти площадь квадрата, прямоугольника, параллелограмма, ромба? Какие еще формулы для вычисления площади параллелограмма вы знаете?
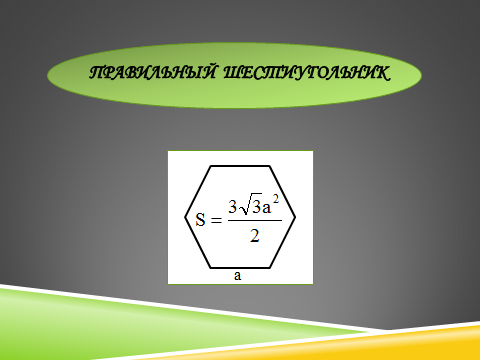
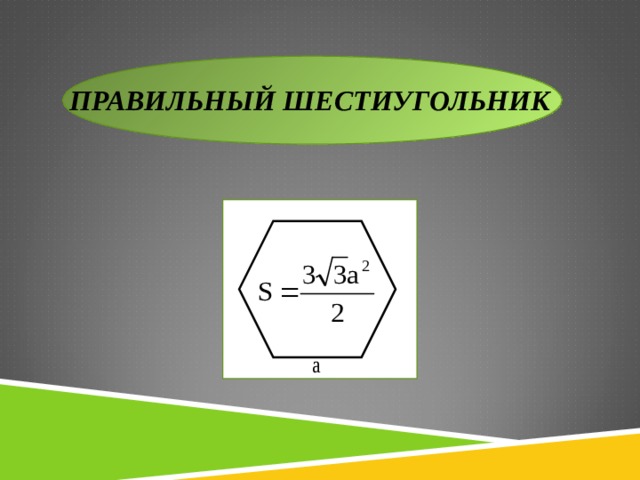
Как найти площадь правильного шестиугольника?
Давайте также вспомним еще ряд соотношений, необходимых для успешности как сегодняшнего урока, так и для решения задач по геометрии в целом.
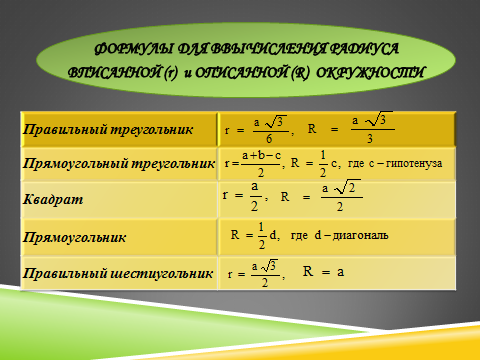
С помощью каких формул можно вычислить радиусы описанной и вписанной окружностей для
Для решения задач нам также потребуются некоторые отношения подобия.
Как найти коэффициент подобия для подобных многоугольников, для кругов?
Чему равно отношение периметров подобных многоугольников?
Чему равно отношение площадей подобных фигур?
Чему равно отношение объемов подобных тел?
Ответьте, пожалуйста, ещё на ряд вопросов.
Во сколько раз увеличится площадь треугольника, если его стороны увеличить в 3 раза?
Во сколько раз увеличится площадь прямоугольного треугольника, если один из катетов увеличить в 5 раз?
Как изменится площадь квадрата, если его стороны уменьшить в 4 раза?
Как изменится площадь прямоугольника, если одну из его сторон увеличить в 2 раза, обе стороны увеличить в 2 раза?
Как изменится площадь правильного шестиугольника, если его стороны уменьшить в 1,5 раза?
Как изменится объем призмы, если все ребра уменьшить в 3 раза; если стороны основания уменьшить в 3 раза, а высоту оставить неизменной?
Как изменится объем цилиндра, если увеличить его высоту в 7 раз, а основание оставить прежним?
Представьте себе ситуацию: воду из одного сосуда переливают во второй сосуд, дно которого с коэффициентом 2 подобно дну первого сосуда. Как изменится при этом уровень воды?
III . Решение тренировочных упражнений.
Итак, всю необходимую теорию мы повторили, приступаем к решению задач.
Одним из пунктов домашнего задания был выбор из прототипов открытого банка ЕГЭ заданий на вычисление объема прямой призмы и цилиндра и распределение их по группам. Какие группы вы получили, и какие задания отнесли к той или иной группе?
Для удобства я выделила эти задачи в отдельный блок (задания для классной работы) (Приложение 1). При отборе задач кое-кто из вас, вероятно, уже «прикинул», как они решаются. Кто хочет проверить свои силы и решить несколько аналогичных задач самостоятельно? Раздать варианты задач для самостоятельного решения (решить не менее любых пяти из десяти предложенных). (Приложение 2)
Ну а с остальными поработаем вместе.
Прежде чем мы приступим к решению, три ученика пойдут к доске и оформят решение задач на вычисление объема части цилиндра на доске, это задачи 7 – 9.
Дополнительный вопрос: с чем совпадает высота прямой призмы?
Ученик комментирует решение с места, краткая запись появляется на экране.
(для определения объема тела лучше всего подходит способ, изобретенный еще Архимедом: будучи погруженным в жидкость, тело вытесняет ровно столько, сколько и составляет его объем ).
(выразим измерения второго цилиндра через измерения первого и упростим получившееся выражение, отделим произведение, равное объёму первого цилиндра и вычислим объем второго)
(прокомментировав решение, ученики садятся, все остальные записывают решение задач в тетради)
Прежде чем приступить к решению следующих задач, давайте вспомним, какая призма называется вписанной в цилиндр? Какую призму можно вписать в цилиндр?
Какие конфигурации тел чаще всего встречаются в задачах ЕГЭ?
Какую призму называют описанной около цилиндра? Какую призму можно описать около цилиндра?
Ну а теперь поменяемся местами. Те учащиеся, кто работал самостоятельно, отложите работы, чуть позже мы их проверим, а те ребята, которые работали вместе со мной, проверят свои силы при выполнении самостоятельной работы. Перед вами лежат задания в двух вариантах, в каждом варианте по десять задач. Вам необходимо решить не менее трех из них. Какие задачи выполнить – выбирайте сами.
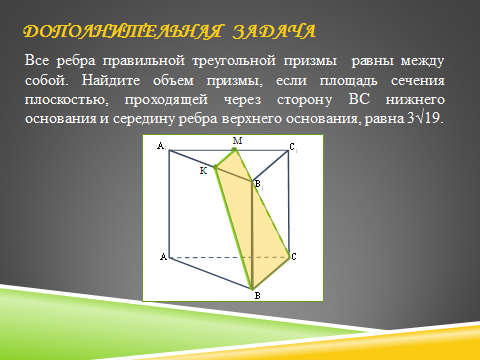
(более сильной группе ребят выдать тексты дополнительной задачи с изображением призмы) (Приложение 3)
Читайте также: Расположение цилиндров камаз 5320 схема
Все ребра правильной треугольной призмы 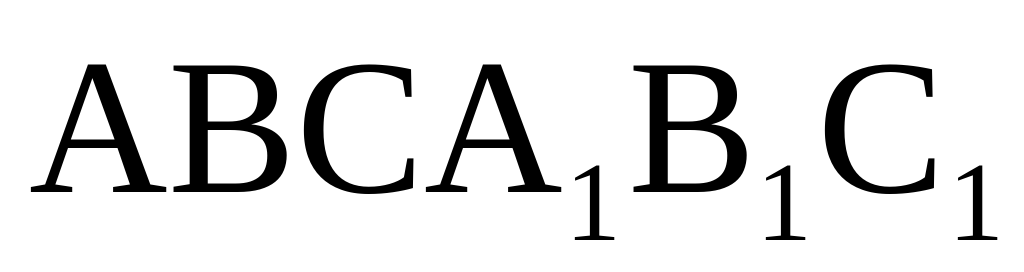
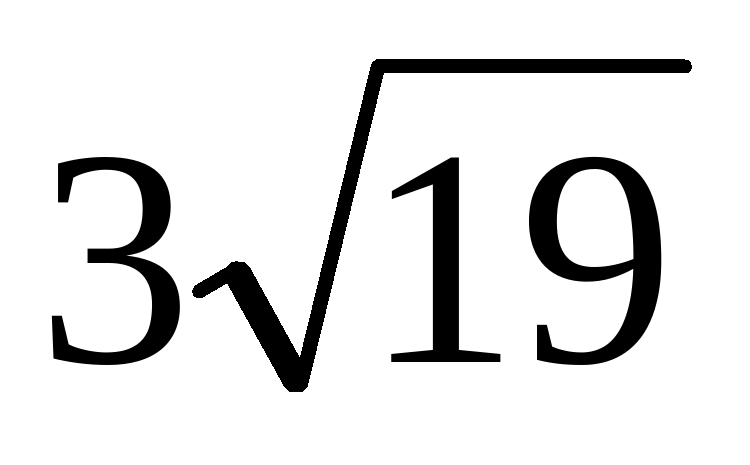
Итак, вы ознакомились с условием задачи, решать на уроке мы её не будем, но чтобы вы дома успешно с ней справились, давайте составим план решения.
Первый пункт лежит на поверхности и мы его выполним:
(Пусть К – середина ребра А1В1. Точки В и К лежат в одной плоскости, соединим их. Так как плоскости АВС и А1В1С1 параллельны, то секущая плоскость пересекает их по параллельным прямым. Через точку К проведем прямую, параллельную ВС, пусть она пересекает ребро А1С1 в точке М. Точки М и С лежат в одной плоскости, мы их соединяем).
Учащиеся высказывают предположения о дальнейшем ходе решения, учитель производит корректировку.
IV . Подведение итогов. Рефлексия.
Итак, занятие подходит к концу. Давайте подведем итоги. Каждый из вас сегодня поработал самостоятельно. Возьмите ваши работы, поменяйтесь с рядом сидящим, оцените работы друг друга. Вспомните, отвечал ли ваш товарищ сегодня устно, сколько раз он отвечал, правильно ли. Добавьте по баллу за каждый правильный ответ.
Если ваш товарищ набрал 5 баллов и больше, поставьте ему «5» (отлично)
3 балла – «3» (удовлетворительно)
Кто получил отметку отлично, хорошо? Есть такие, чья работа была неудовлетворительной?
Попробуйте дома разобраться в своих ошибках, выяснить причину, по которой вы их допустили.
Ну а сейчас мне хотелось бы, чтобы каждый из вас определил, на какой ступеньке изучения данной темы он находится?
Есть стоящие лишь на первой ступени? На последней ступени? Сделайте соответствующие выводы.
V . Информирование о домашнем задании. (Приложение 4)
Просмотр содержимого документа
«Приложение 1»
Прототипы задачи 8 из открытого банка ЕГЭ по математике
по теме «Объем прямой призмы и цилиндра»
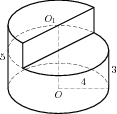
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Найдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны .
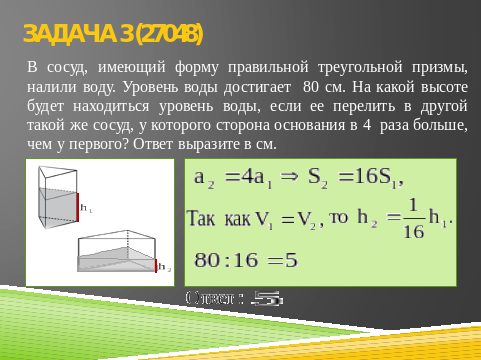
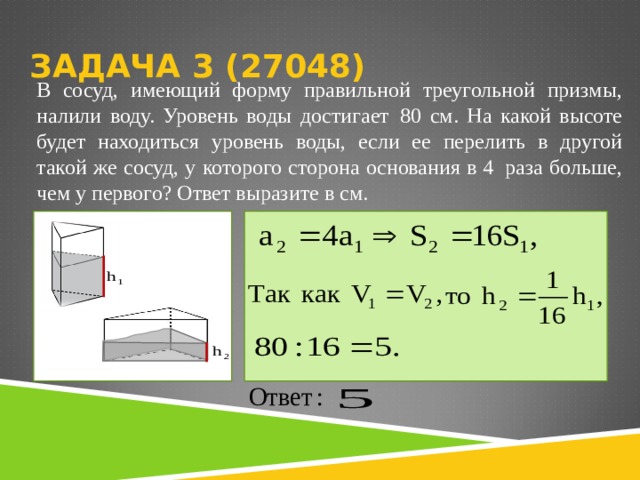
В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см.
В сосуд, имеющий форму правильной треугольной призмы, налили 2300 см 3 воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 27 см. Чему равен объем детали? Ответ выразите в см 3 .
В цилиндрический сосуд, в котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали? Ответ выразите в литрах.
Объем первого цилиндра равен 12 м 3 . У второго цилиндра высота в три раза больше, а радиус основания — в два раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.
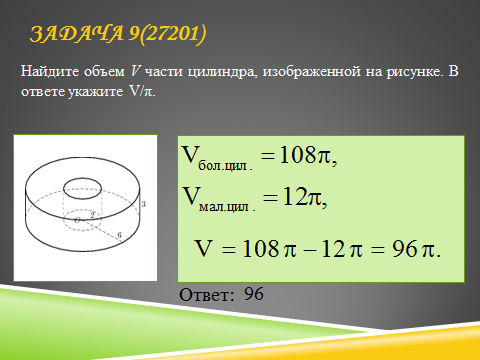
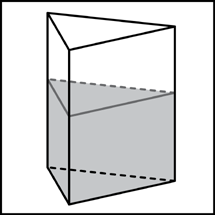
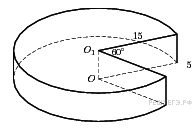
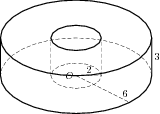
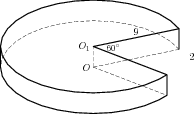
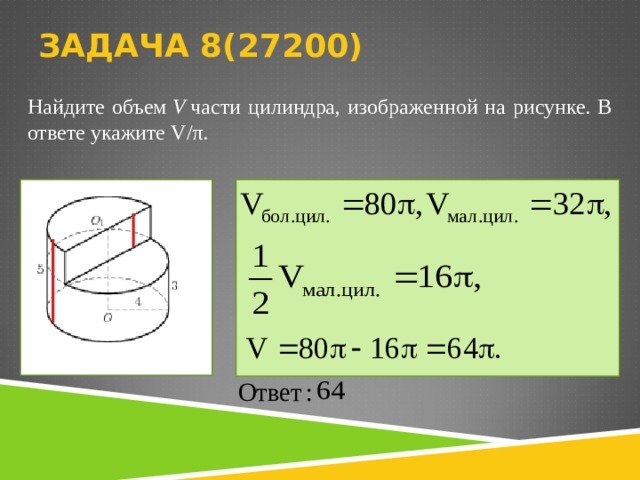
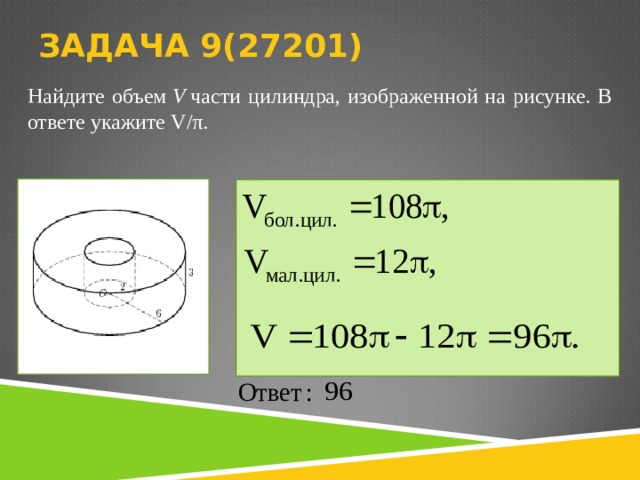
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
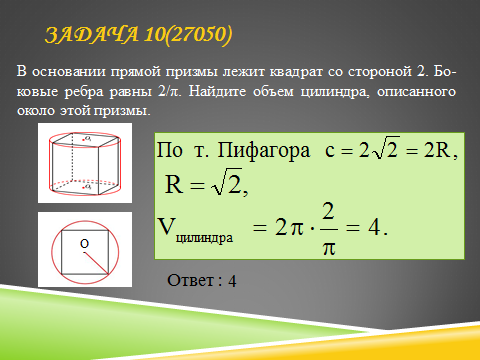
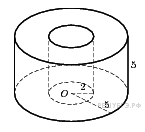
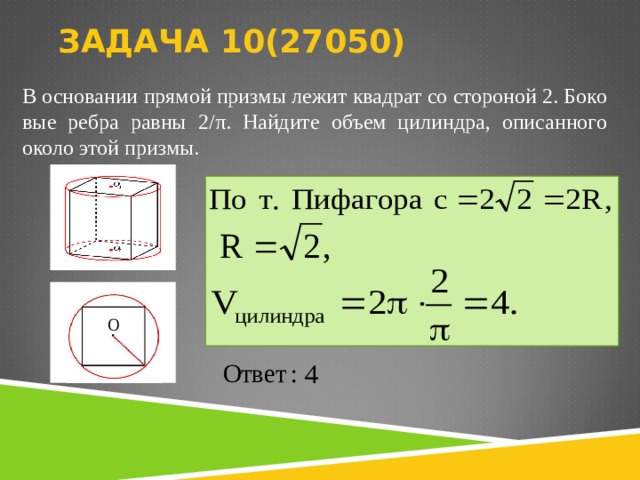
В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
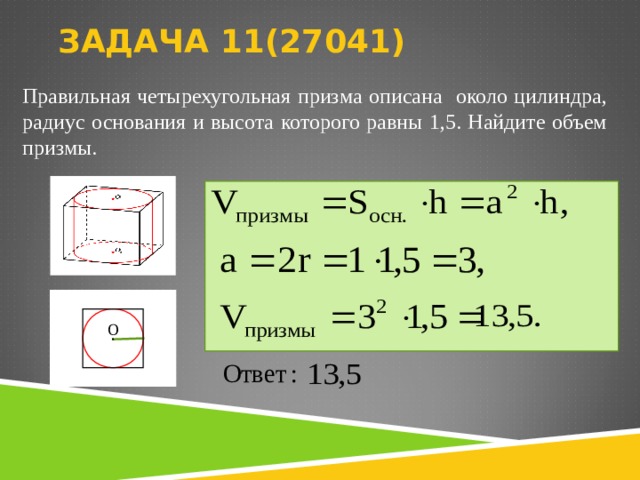
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1,5. Найдите объем призмы.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро.
Найдите объем правильной шестиугольной призмы, все ребра которой равны .
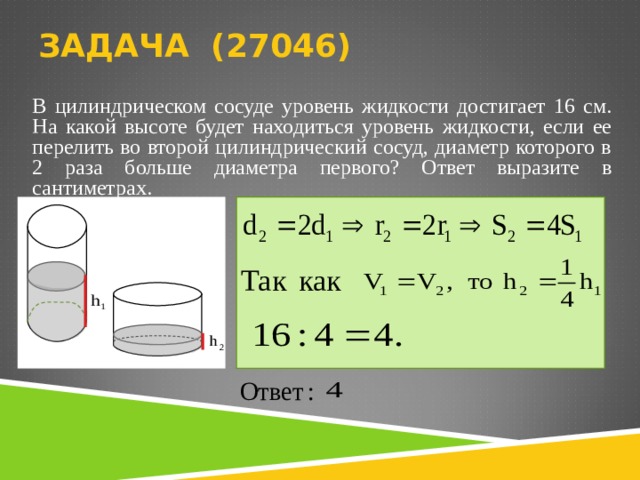
В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах.
В цилиндрический сосуд налили 2000 см³. Уровень жидкости оказался равным 12 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в см³.
Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен 4. Найдите высоту цилиндра, если объем призмы равен 16.
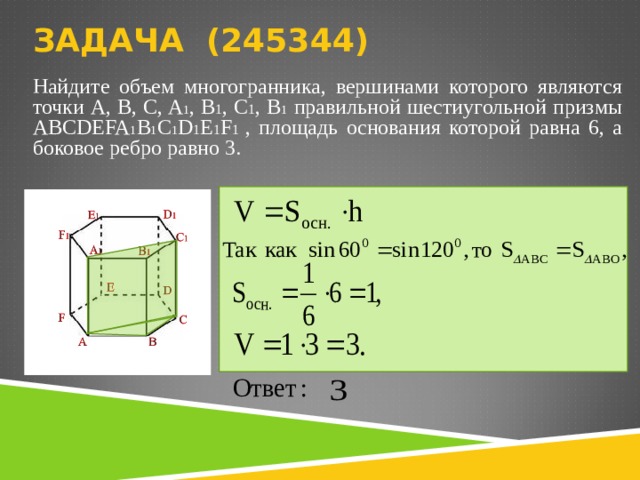
Найдите объем многогранника, вершинами которого являются точки 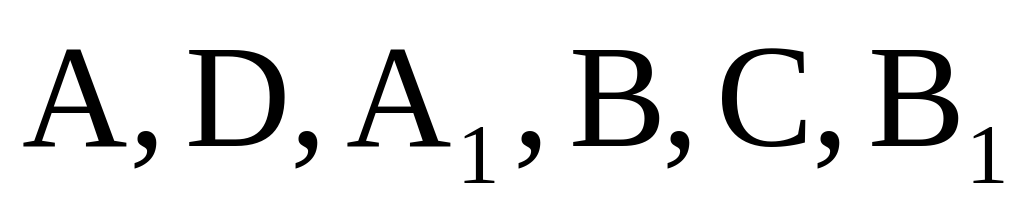
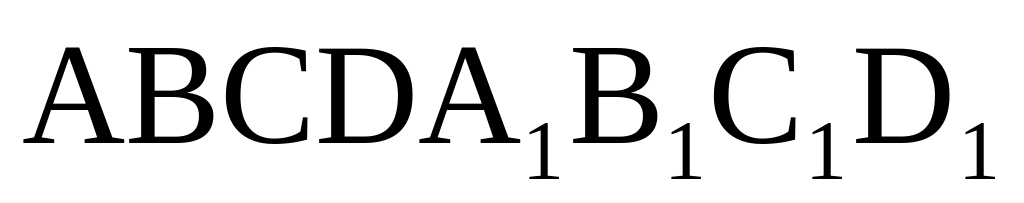
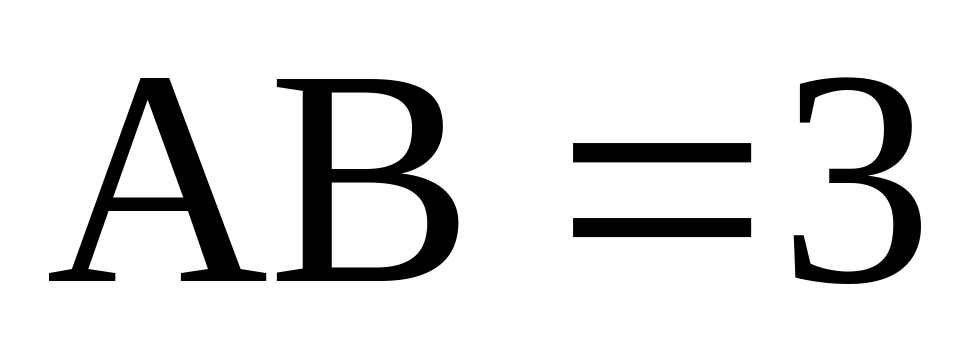
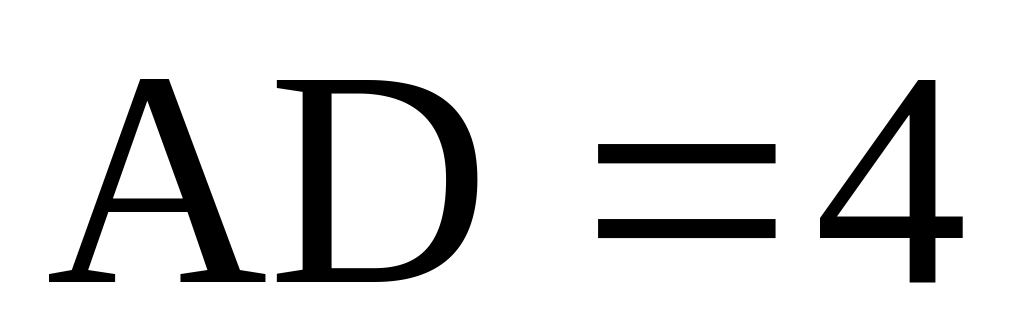
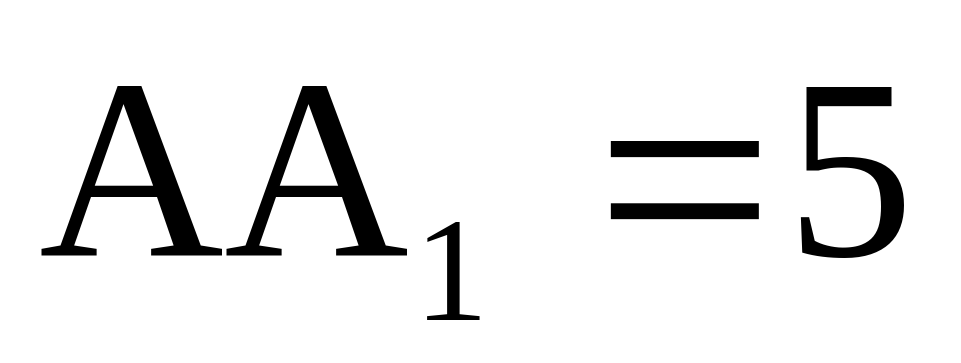
Найдите объем многогранника, вершинами которого являются точки 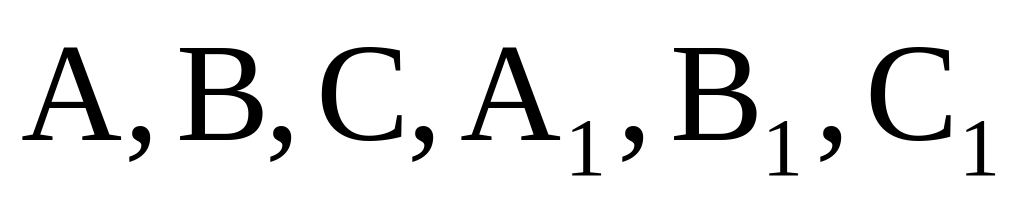
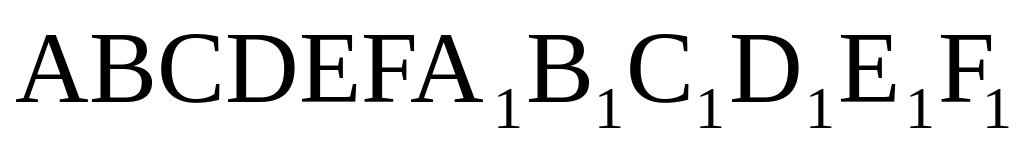
Просмотр содержимого документа
«Приложение 2»
Задания для самостоятельной работы
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 7. Объем призмы равен 87,5. Найдите ее боковое ребро.
Найдите объем правильной шестиугольной призмы, все ребра которой равны .
В цилиндрическом сосуде уровень жидкости достигает 27 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 3 раза больше диаметра первого? Ответ выразите в сантиметрах.
В цилиндрический сосуд налили 1800 см 3 воды. Уровень жидкости оказался равным 12 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 2 см. Чему равен объем детали? Ответ выразите в см 3 .
Одна цилиндрическая кружка вдвое выше второй, зато вторая в 6 раз шире. Найдите отношение объема второй кружки к объему первой.
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
В основании прямой призмы лежит прямоугольный треугольник с катетами 9 и 6. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен 1. Найдите высоту цилиндра, если объем призмы равен 5.
Найдите объем многогранника, вершинами которого являются точки 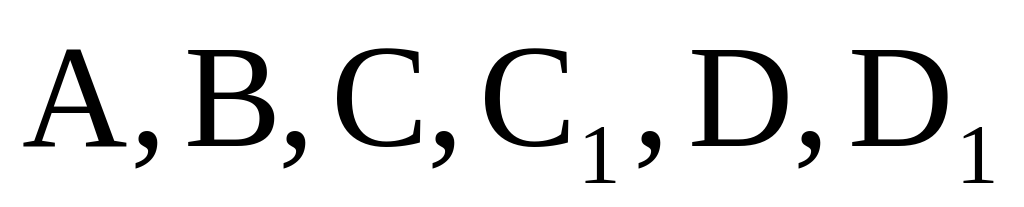
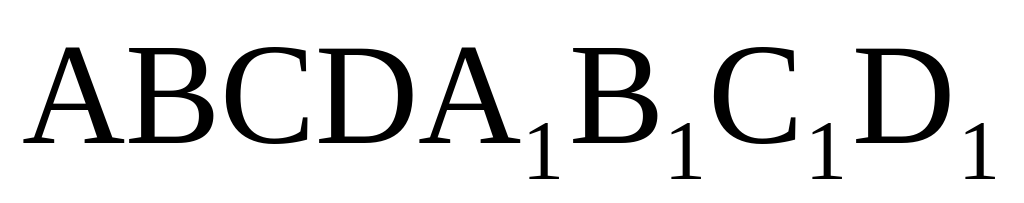
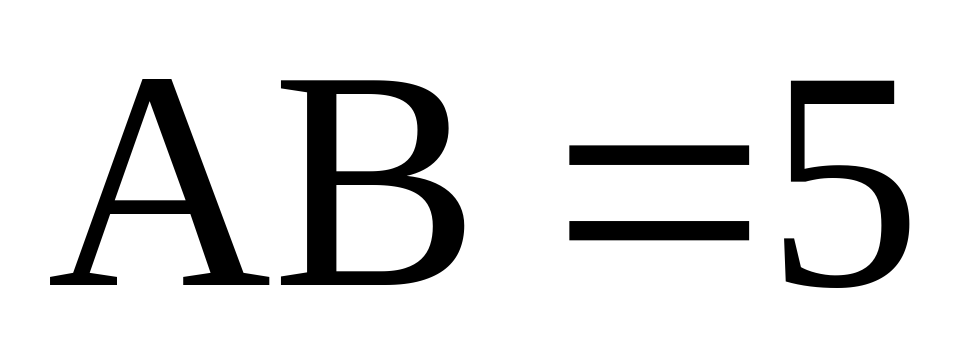
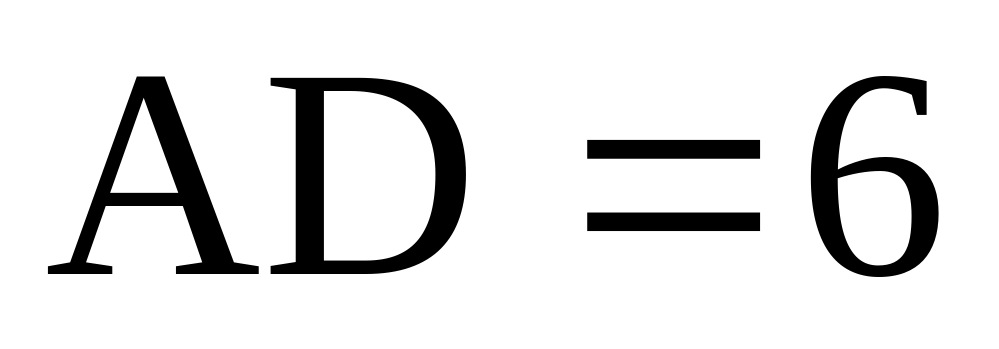
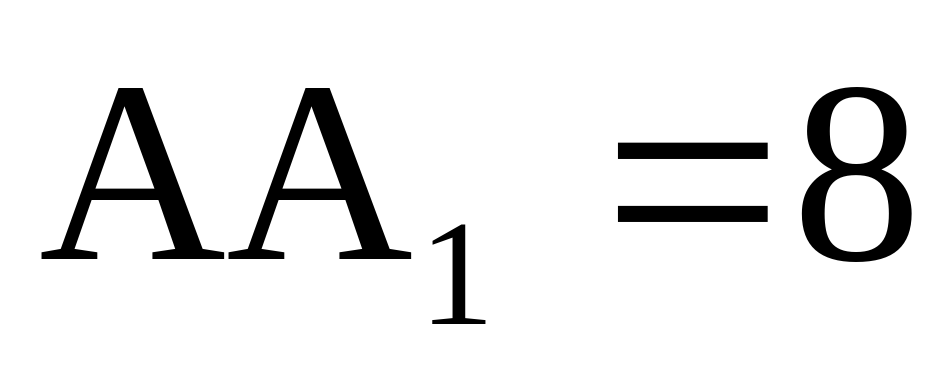
Найдите объем многогранника, вершинами которого являются точки 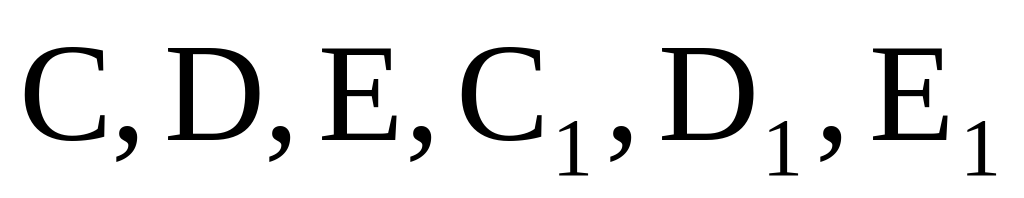
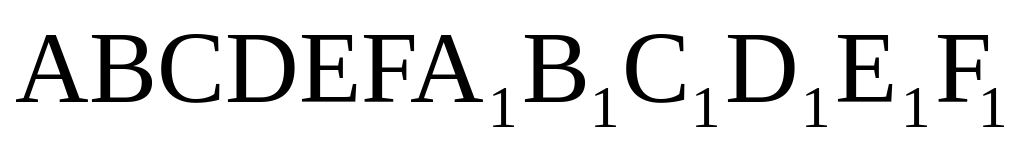
Задания для самостоятельной работы
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 2 и 7. Объем призмы равен 42. Найдите ее боковое ребро.
Найдите объем правильной шестиугольной призмы, все ребра которой равны .
В цилиндрическом сосуде уровень жидкости достигает 48 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 4 раза больше диаметра первого? Ответ выразите в сантиметрах.
В цилиндрический сосуд налили 1200 см 3 воды. Уровень жидкости оказался равным 15 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 12 см. Чему равен объем детали? Ответ выразите в см 3 .
Одна цилиндрическая кружка вдвое выше второй, зато вторая в 8 раз шире. Найдите отношение объема второй кружки к объему первой.
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
В основании прямой призмы лежит прямоугольный треугольник с катетами 7 и 8. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен 9. Найдите высоту цилиндра, если объем призмы равен 81.
Найдите объем многогранника, вершинами которого являются точки 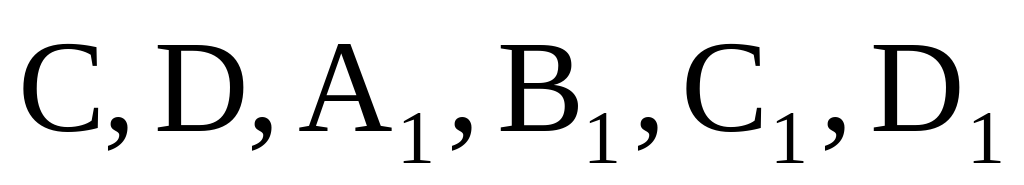
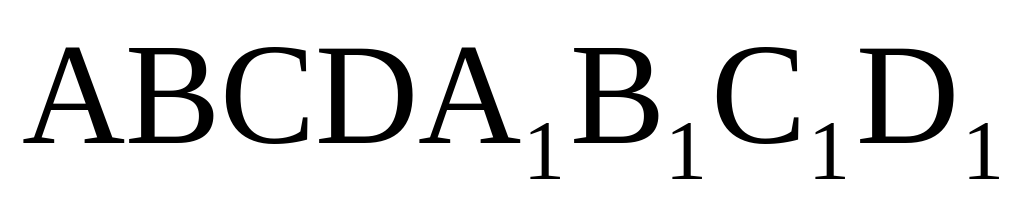
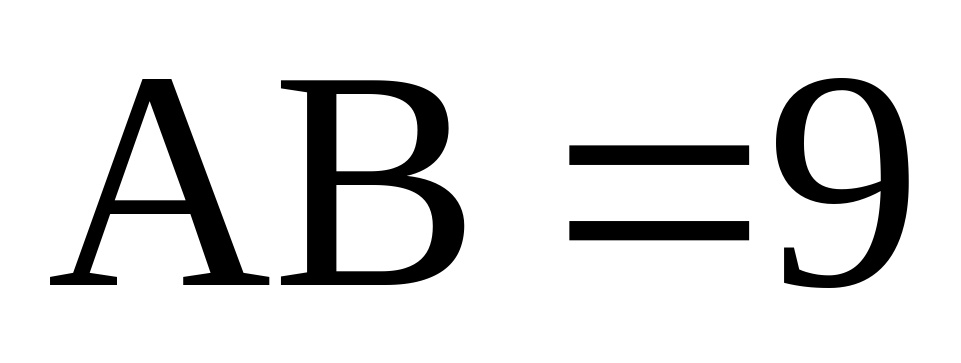
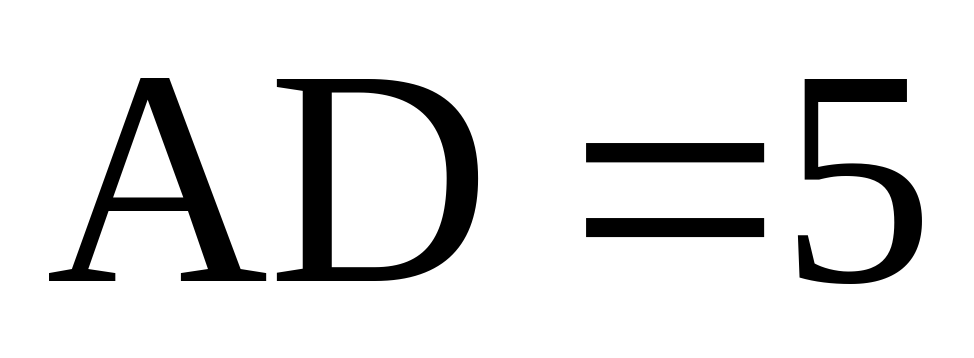
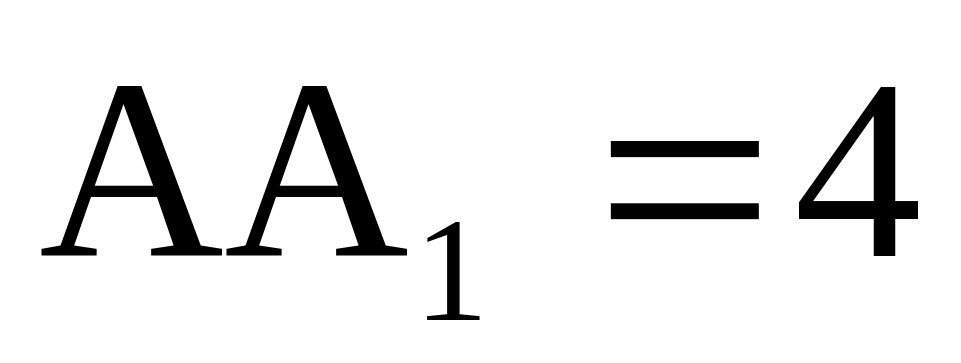
Найдите объем многогранника, вершинами которого являются точки 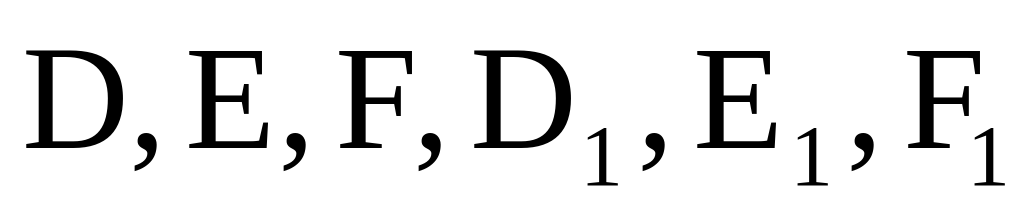
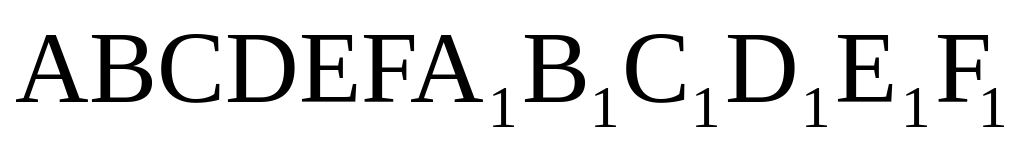
Читайте также: Что такое шнек цилиндр
Просмотр содержимого документа
«Приложение 3»
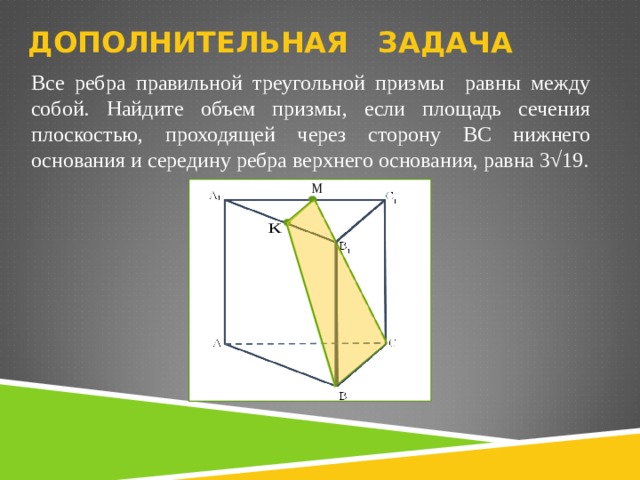
Все ребра правильной треугольной призмы 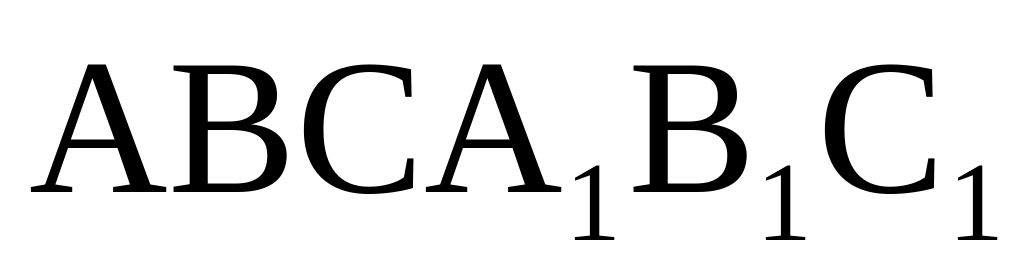
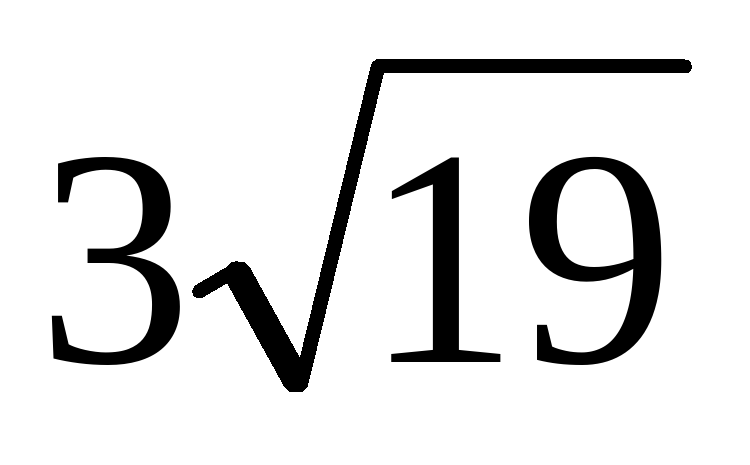
Все ребра правильной треугольной призмы 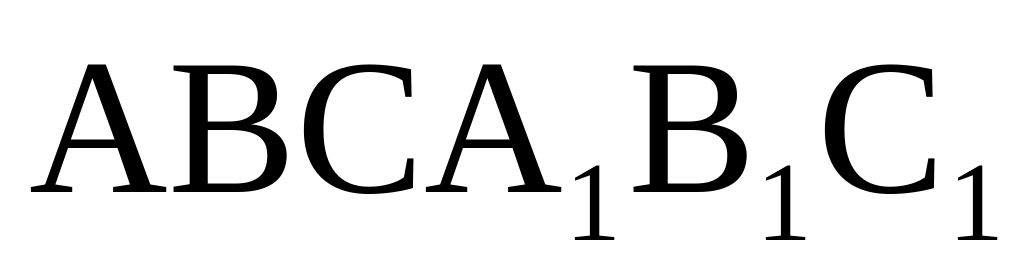
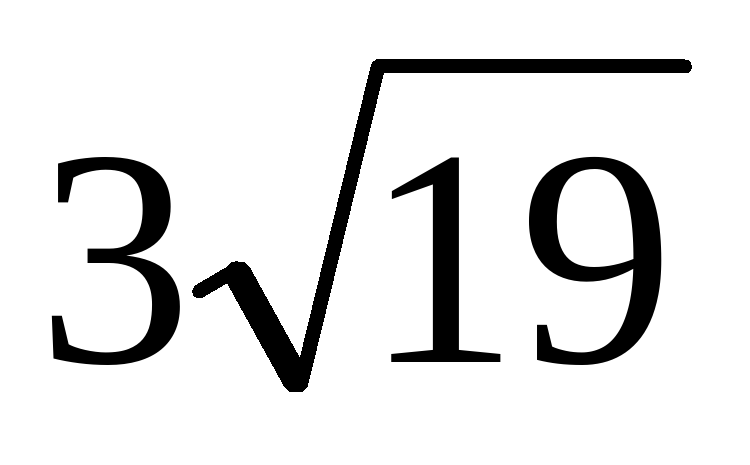
Просмотр содержимого документа
«Приложение 4»
Задачи для домашней работы
В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 18 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 3 раза больше, чем у первого? Ответ выразите в сантиметрах.
В сосуд, имеющий форму правильной треугольной призмы, налили 1500 см 3 воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 28 см. Чему равен объем детали? Ответ выразите в см 3 .
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 2 и 3. Объем призмы равен 18. Найдите ее боковое ребро.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 7, боковое ребро равно 4. Найдите объем призмы.
Найдите объем правильной шестиугольной призмы, стороны основания которой равны 9, а боковые ребра равны .
В цилиндрическом сосуде уровень жидкости достигает 8 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах.
В цилиндрический сосуд налили 1200 см 3 воды. Уровень жидкости оказался равным 12 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 10 см. Чему равен объем детали? Ответ выразите в см 3 .
В цилиндрический сосуд, в котором находится 10 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,9 раза. Чему равен объем детали? Ответ выразите в литрах.
Объем первого цилиндра равен 81 м 3 . У второго цилиндра высота в 4 раза больше, а радиус основания — в 3 раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.
Одна цилиндрическая кружка вдвое выше второй, зато вторая в 3 раза шире. Найдите отношение объема второй кружки к объему первой.
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
В основании прямой призмы лежит прямоугольный треугольник с катетами 4 и 1. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
В основании прямой призмы лежит квадрат со стороной 7. Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 9,5. Найдите объем призмы.
Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен 3. Найдите высоту цилиндра, если объем призмы равен 18.
Найдите объем многогранника, вершинами которого являются точки 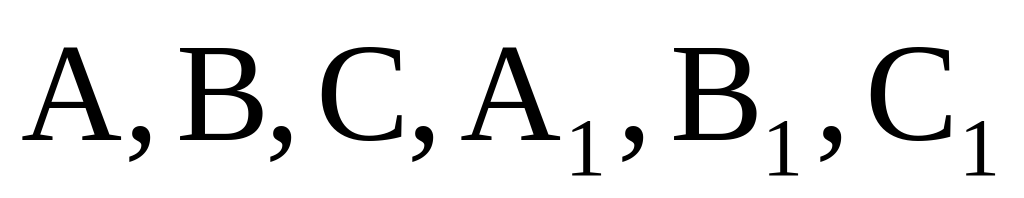
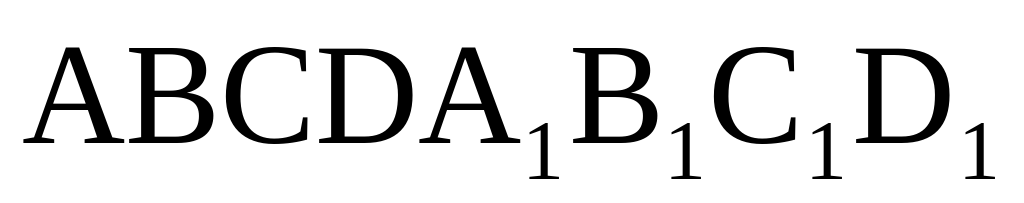
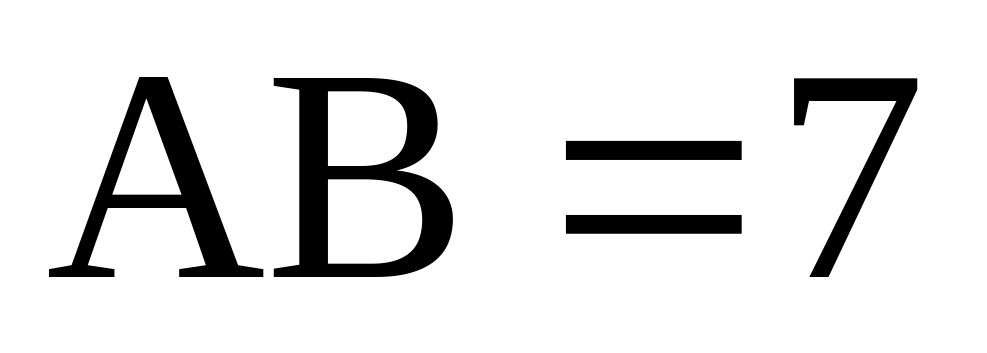
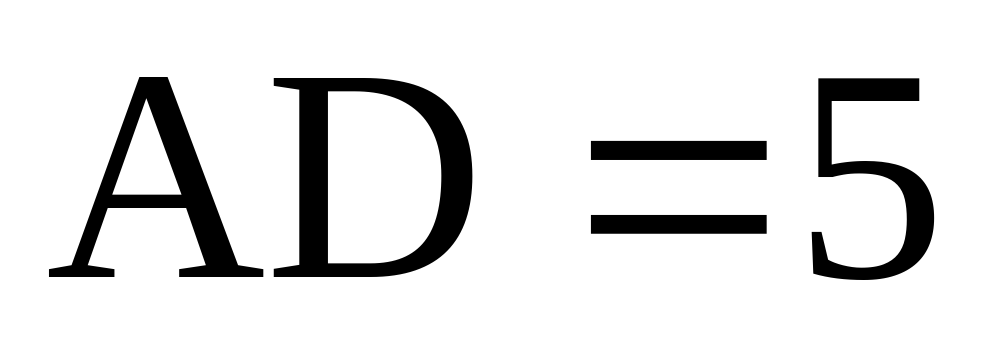
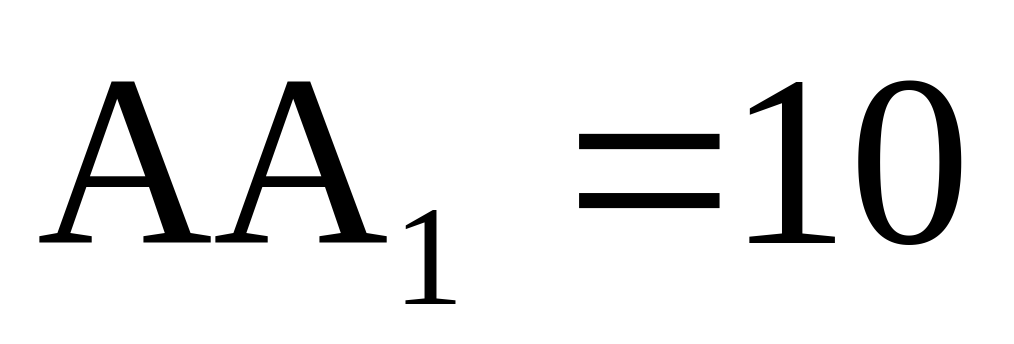
Найдите объем многогранника, вершинами которого являются точки 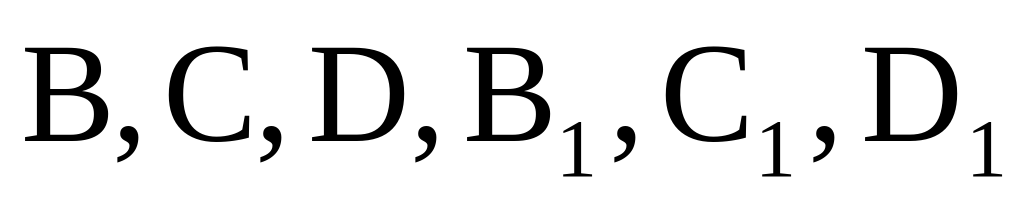
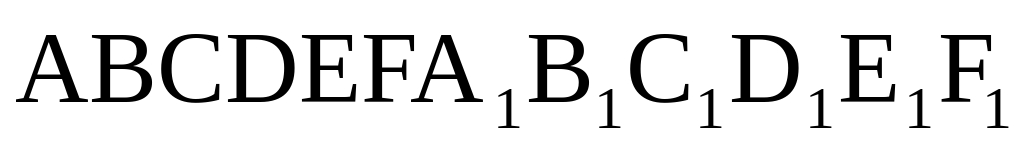
Просмотр содержимого презентации
«Презентация»
Курылева С.С., учитель математики
Первое условие, которое надлежит
это быть точным, второе – быть
( французский государственный и военный
- повторить формулы для вычисления объема прямой призмы и цилиндра;
- учиться применять формулы для вычисления объема прямой призмы и цилиндра при решении задач;
- рассмотреть задачи на вычисление объема призмы, вписанной в цилиндр и призмы, описанной около цилиндра.
РАДИУСА ВПИСАННОЙ И ОПИСАННОЙ ОКРУЖНОСТИ
НЕКОТОРЫЕ ОТНОШЕНИЯ ПОДОБИЯ
- Отношение периметров подобных многоугольников равно коэффициенту подобия.
- Отношение площадей подобных фигур равно квадрату коэффициента подобия.
- Отношение объемов подобных тел равно кубу коэффициента подобия.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы .
Найдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны √3.
В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см.
В сосуд, имеющий форму правильной треугольной призмы, налили 2300 см³ воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 27 см. Чему равен объем детали? Ответ выразите в см³.
В цилиндрический сосуд, в котором находится 6 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объем детали? Ответ выразите в литрах.
Объем первого цилиндра равен 12 м 3 . У второго цилиндра высота в три раза больше, а радиус основания — в два раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/ π .
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/ π .
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/ π .
ПРИЗМА, ВПИСАННАЯ В ЦИЛИНДР
ПРИЗМЫ, ВПИСАННЫЕ В ЦИЛИНДР
В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны 2/ π . Найдите объем цилиндра, описанного около этой призмы.
ПРИЗМА, ОПИСАННАЯ ОКОЛО ЦИЛИНДРА
ПРИЗМЫ, ОПИСАННЫЕ ОКОЛО ЦИЛИНДРА
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1,5. Найдите объем призмы.
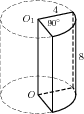
Все ребра правильной треугольной призмы равны между собой. Найдите объем призмы, если площадь сечения плоскостью, проходящей через сторону BC нижнего основания и середину ребра верхнего основания, равна 3√19.
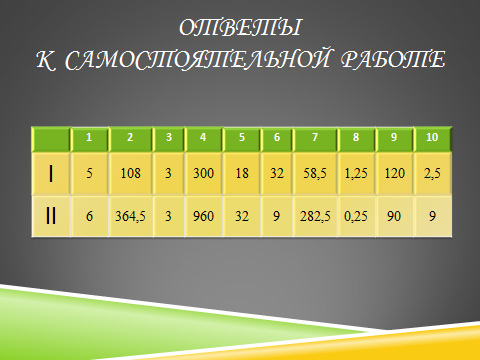
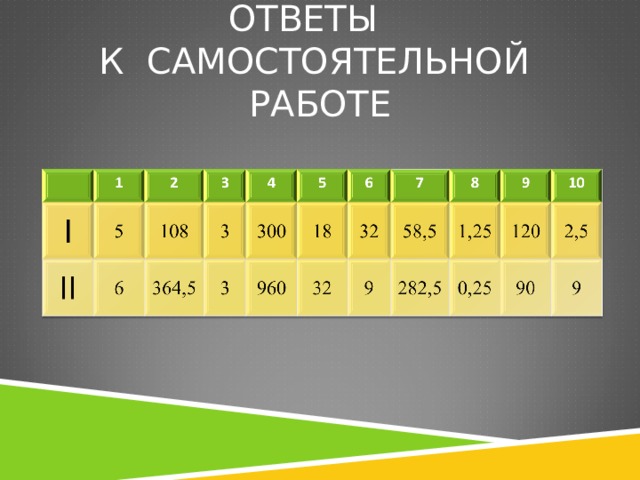
ОТВЕТЫ К САМОСТОЯТЕЛЬНОЙ РАБОТЕ
Просмотр содержимого презентации
«Приложение 5»
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро.
Найдите объем многогранника, вершинами которого являются точки A, D, A 1 , B, C, B 1 , прямоугольного параллелепипеда ABCDA 1 B 1 C 1 D 1 , у которого AB=3, AD=4, AA 1 =5.
Найдите объем многогранника, вершинами которого являются точки A, B, C, A 1 , B 1 , C 1 , B 1 правильной шестиугольной призмы ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 , площадь основания которой равна 6, а боковое ребро равно 3 .
В цилиндрический сосуд налили 2000 см³. Уровень жидкости оказался равным 12 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в см³.
В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в сантиметрах.
Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/ π .
В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны 5/ π . Найдите объем цилиндра, описанного около этой призмы.
Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен 4. Найдите высоту цилиндра, если объем призмы равен 16.
📺 Видео
ЕГЭ. Задача 8. Призма и цилиндрСкачать

11 класс. Геометрия. Объем цилиндраСкачать

Геометрия 11 класс (Урок№12 - Объемы прямой призмы и цилиндра.)Скачать

Геометрия 11 класс: Объем призмы и цилиндра. ВидеоурокСкачать

11 класс, 31 урок, Объем прямой призмыСкачать

Призма и цилиндр. Практическая часть. 11 класс.Скачать

Объем призмы. Практическая часть. 11 класс.Скачать

Параллелепипед описан около цилиндраСкачать

Объем цилиндра. Практическая часть. 11 класс.Скачать

Видеоурок по математике "Цилиндр"Скачать

Стереометрия. ЕГЭ. Куб описан около сферы радиуса 1. Найдите объём куба.Скачать

Миникурс по геометрии. Куб, призма, цилиндр и конусСкачать

В основании прямой призмы лежит прямоугольный треугольник с катетами 5 и 6. Боковые ребра призмы...Скачать

Стереометрия, номер 39.1Скачать