Как найти апофему цилиндра

Видео:10 класс, 33 урок, Правильная пирамидаСкачать

Апофема правильной треугольной пирамиды: формула и пример задачи

При изучении характеристик пространственных фигур в курсе стереометрии большое внимание уделяется таким свойствам, как площадь и объем. В то же время знать линейные параметры фигур важно, чтобы иметь возможность рассчитать указанные свойства. В данной статье ответим на вопрос, как найти апофему пирамиды правильной треугольной.

Видео:Нахождение апофемы пирамидыСкачать

Какая фигура будет рассмотрена?

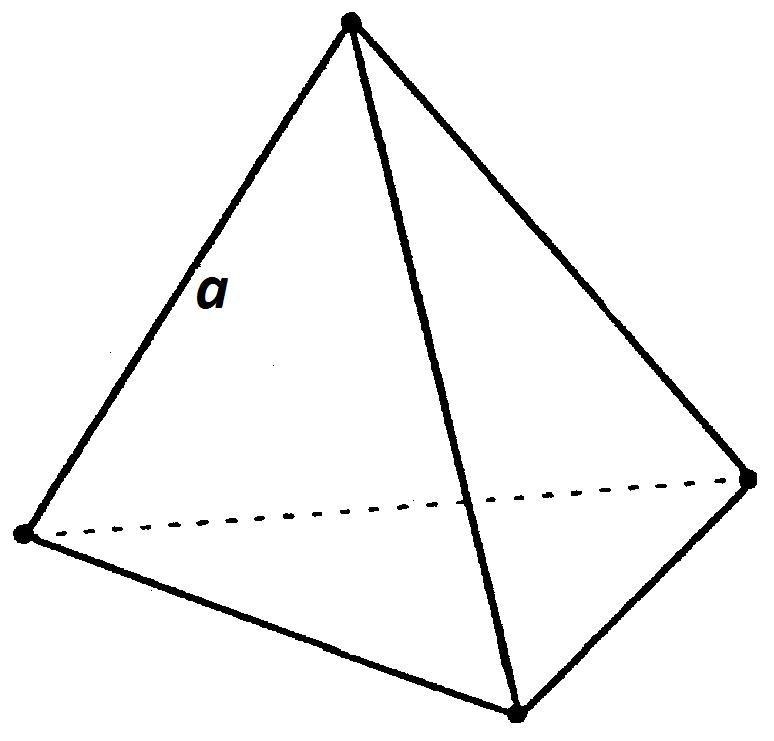
Треугольная пирамида с правильным основанием представляет собой фигуру в пространстве, которая ограничена одним равносторонним треугольником (основание) и тремя равнобедренными треугольниками (боковые стороны). Чтобы иметь возможность более четко представить эту пирамиду, покажем ее на рисунке.

Важной точкой любой пирамиды является ее вершина, которая не принадлежит основанию. Если опустить перпендикуляр из нее на основание, то его длина будет высотой фигуры. В дальнейшем будем обозначать высоту буквой h. Высота правильной пирамиды падает точно в геометрический центр треугольника (точка пересечения его медиан, а также биссектрис и высот). Вторым линейным параметром, который следует знать, является длина стороны основания треугольной пирамиды, то есть длина стороны равностороннего треугольника. Обозначим ее буквой a.

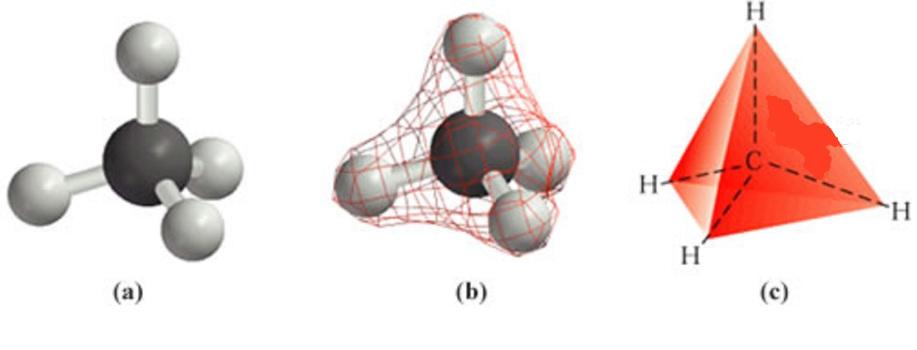
Треугольная пирамида имеет собственное название — тетраэдр. Тетраэдр не является чисто теоретической геометрической фигурой. Она также встречается в некоторых природных структурах. Так, в алмазе атом углерода соединен с четырьмя такими же атомами, которые образуют тетраэдр. Другой пример — это молекула метана, в которой углерод, соединенный с четырьмя атомами водорода, образует правильную треугольную пирамиду.

Видео:КАК НАЙТИ ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПИРАМИДЫ?Скачать

Формула апофемы пирамиды правильной треугольной

Перейдем непосредственно к вопросу статьи. Для треугольной пирамиды правильной апофемой называется любая из высот боковых треугольников, опущенная из вершины фигуры. Обозначим ее hb. Поскольку рассматриваемая фигура состоит из трех боковых треугольников, которые равны друг другу, то она имеет три одинаковых апофемы hb.

Определение длины апофемы не составляет большого труда. Предположим, что высота h и длина стороны a известны. Проводим высоту фигуры и рассматриваем треугольник прямоугольный, который находится внутри пирамиды и образован следующими сторонами:

• апофемой hb (гипотенуза);
• высотой h (один катет);
• 1/3 медианы m равностороннего треугольника (второй катет).

Длина медианы m треугольника в основании равна:

Пользуясь теоремой Пифагора, получаем формулу для длины апофемы hb:

Эта формула показывает, что длина апофемы hb для любых параметров треугольной пирамиды всегда больше ее высоты h.

Видео:Как найти объем. Принцип Кавальери | Ботай со мной #050 | Борис Трушин |Скачать

Решение задачи на определение значения hb

Решим интересную задачу. Рассчитаем длину апофемы для тетраэдра, у которого все ребра равны друг другу.

Обозначим длину ребра буквой a. Она же является стороной треугольника в основании. Чтобы определить hb, необходимо найти h. Сделать это не сложно, если рассмотреть прямоугольный треугольник, образованный высотой h, ребром a и двумя третями медианы m. Получаем:

h = √(a2 — 4/9*m2) = √(a2 — 4/9*3/4*a2) = a*√(2/3)

Теперь применяем формулу для апофемы, получаем:

hb = √(a2/12 + h2) = √(a2/12 + 2/3*a2) = √3/2*a

Мы получили очевидный результат. Апофема правильной пирамиды треугольной равна длине медианы любого из равносторонних треугольников.

Читайте также: Лепка человека в старшей группе из цилиндра

Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Апофема и сторона основания правильной пирамиды

Видео:Миникурс по геометрии. Куб, призма, цилиндр и конусСкачать

Свойства

Периметр основания правильной пирамиды равен произведению длины стороны основания на их удвоенное количество, а площадь – отношению количества сторон, умноженных на квадрат стороны, к четырем тангенсам угла из 180 градусов, деленных на количество сторон в основании. P=n(a+b) S=(na^2)/(4 tan⁡〖(180°)/n〗 )

Радиус окружности, вписанной в правильный многоугольник, являющимся основанием правильной пирамиды, равен отношению стороны к двум тангенсам того же угла, а радиус окружности, описанной вокруг такого многоугольника, — отношению стороны к двум синусам. (рис.34.1,34.2) r=a/(2 tan⁡〖(180°)/n〗 ) R=a/(2 sin⁡〖(180°)/n〗 )

Чтобы найти внутренний угол многоугольника в основании правильной пирамиды, нужно умножить 180 градусов на отношение разности количества сторон и двух единиц к самому количеству сторон такого многоугольника. (рис.34.3) γ=180°(n-2)/n

Зная апофему и сторону основания правильной пирамиды, можно найти боковое ребро и высоту пирамиды из прямоугольных треугольников, образованных ими, через теорему Пифагора. (рис.34.4, 35.1) h=√(l^2-r^2 )=√(l^2-(a/(2 tan⁡〖(180°)/n〗 ))^2 ) b=√(l^2+a^2/4)

Угол между апофемой и основанием легко вычислить, найдя его косинус, который равен отношению радиуса вписанной в основание окружности к апофеме, и воспользовавшись таблицами Брадиса. Угол между боковым ребром и основанием находится аналогично через косинус, как отношение радиуса окружности, описанной вокруг основания, к боковому ребру. (рис.34.4, 34.5) cos⁡α=R/b=a/(2 sin⁡〖(180°)/n〗 √(l^2+a^2/4)) cos⁡β=r/l=a/(2l tan⁡〖(180°)/n〗 )

Чтобы найти площадь боковой поверхности пирамиды через апофему и сторону основания, необходимо сначала найти площадь одной ее грани-треугольника, и затем умножить ее на количество граней – сторон в основании. Площадь полной поверхности пирамиды будет равна сумме площади боковой поверхности и площади основания. S_(б.п.)=lan/2 S_(п.п.)=an(l/2+a/(4 tan⁡〖(180°)/n〗 ))

Объем правильной пирамиды равен произведению площади основания на высоту, деленному на три. Подставив необходимое выражение вместо площади основания и высоты, получим форму объема пирамиды через апофему и сторону основания. V=1/3 S_(осн.) h=(na^2 √(l^2-(a/(2 tan⁡〖(180°)/n〗 ))^2 ))/(12 tan⁡〖(180°)/n〗 )

Чтобы вписать в правильную пирамиду сферу, ее радиус должен быть равен трем объемам, деленным на площадь полной поверхности пирамиды, а чтобы описать такую же сферу вокруг пирамиды, нужно чтобы ее радиус совпадал с отношением квадрата бокового ребра к двум высотам такой пирамиды. (рис.34.6, 34.7) r_1=3V/S_(п.п.) =(na^2 √(l^2-(a/(2 tan⁡〖(180°)/n〗 ))^2 ))/(4 tan⁡〖(180°)/n〗 (2l+a/tan⁡〖(180°)/n〗 ) ) R_1=b^2/2h=(4l^2+a^2)/(8√(l^2-(a/(2 tan⁡〖(180°)/n〗 ))^2 ))

Видео:10 класс, 34 урок, Усеченная пирамидаСкачать

Стороны и апофема усеченной пирамиды

Видео:Призма и пирамида. Площадь и объем. Вебинар | Математика 10 классСкачать

Свойства

Стороны оснований правильной усеченной пирамиды дают возможность вычислить все, что связано с основаниями, используя формулы для правильных многоугольников. Среди таких параметров можно перечислить внутренний угол многоугольника, его периметр, площадь, радиус окружности, вписанной в основание, и радиус окружности, которая может быть описана около него. γ=180°(n-2)/n P=n(a+b+d) S_a=(na^2)/(4 tan⁡〖(180°)/n〗 ) S_b=(nb^2)/(4 tan⁡〖(180°)/n〗 ) r_a=a/(2 tan⁡〖(180°)/n〗 ) r_b=b/(2 tan⁡〖(180°)/n〗 ) R_a=a/(2 sin⁡〖(180°)/n〗 ) R_b=a/(2 sin⁡〖(180°)/n〗 )

Зная апофему усеченной пирамиды, можно вычислить боковое ребро через прямоугольную трапецию, которая их связывает по боковой грани пирамиды. Основаниями такой трапеции являются половины сторон оснований пирамиды, поэтому по прямоугольному треугольнику боковое ребро будет равно радикалу из теоремы Пифагора. (рис. 50.2) d=√(f^2+(b/2-a/2)^2 )=√(f^2+(b-a)^2/4)

Чтобы вычислить высоту усеченной пирамиды, необходимо найти такую же прямоугольную трапецию во внутреннем пространстве усеченной пирамиды, тогда в такой трапеции и прямоугольном треугольнике высота будет равна аналогичному радикалу через радиусы вписанных в основания окружностей и апофему (рис. 50.4) h=√(f^2-(r_b-r_a )^2 )

Чтобы рассчитать углы при основаниях усеченной пирамиды и апофеме, можно воспользоваться в этой же трапеции/прямоугольном треугольнике тригонометрическими отношениями и принципом суммы углов трапеции. cos⁡β=(r_b-r_a)/f α=180°-β

Углы при основаниях и апофеме усеченной пирамиды можно вычислить в трапеции, которую боковое ребро образует с высотой пирамиды подобным образом, через радиусы вписанных в основания окружностей. (рис. 50.3) cos⁡δ=(R_b-R_a)/d ε=180°-δ

Читайте также: Объем газа в цилиндре постоянен

Площадь боковой поверхности усеченной пирамиды равна произведению количества сторон в основании на апофему и полусумму сторон оснований. Чтобы найти площадь полной поверхности через стороны усеченной пирамиды, нужно прибавить к площади боковой поверхности еще два основания. S_(б.п.)=nf (a+b)/2 S_(п.п.)=S_(б.п.)+S_(осн.1,2)=n(f (a+b)/2+a^2/(4 tan⁡〖(180°)/n〗 )+b^2/(4 tan⁡〖(180°)/n〗 ))

Для того чтобы вычислить объем усеченной пирамиды, необходимо сначала найти высоту через теорему Пифагора, как было указано выше, а затем найти треть произведения высоты на сумму площадей оснований с квадратным корнем из их произведения. V=1/3 h(S_осн1+S_осн2+√(S_осн1 S_осн2 ))

Видео:Объем призмы. Практическая часть. 11 класс.Скачать

Статья на тему «Апофема правильной пирамиды»

Ищем педагогов в команду «Инфоурок»

Апофема правильной пирамиды находится по формуле

f — апофема правильной пирамиды (SF)
n — число сторон правильного многоугольника — основания правильной пирамиды
a — сторона правильного многоугольника (AB или BC или CD или DE или EA) — основания правильной пирамиды
h — высота правильной пирамиды (OS)

Апофема правильной пирамиды выводится из следующих формул

Синим цветом на рисунке изображена вписанная в основание правильной пирамиды окружность. Треугольник SFO прямоугольный. Его стороны: OS — высота правильной пирамиды ( h ), OF — радиус вписанной окружности в правильный многоугольник (основание правильной пирамиды ( r )), SF — апофема правильной пирамиды ( f ). По теореме Пифагора

подставив сюда только радиус вписанной окружности получается формула (1).

Вычислить, найти апофему правильной пирамиды по формуле (1)

Правильная пирамида

Правильная пирамида — пирамида, в основани, которой лежит правильный многоугольник, а высота проходит через центр вписанной окружности в основание.

= na 2 h 12 tg 180 ∘ n V=na2h12tg180 ∘ n

a a — сторона основания пирамиды

n n — количество сторон многоугольника в основании

Правильная треугольная пирамида

Правильная треугольная пирамида — пирамида, у которой основанием является равносторонний треугольник и грани равные равнобедренные треугольники.

a a — сторона основания пирамиды

Правильная четырехугольная пирамида

Правильная четырехугольная пирамида — пирамида, у которой основанием является квадрат и грани равные равнобедренные треугольники.

a a — сторона основания пирамиды

Тетраэдр

Тетраэдр — пирамида, у которой все грани — равносторонние треугольники.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Номер материала: ДБ-1705421

Международная дистанционная олимпиада Осень 2021

Вам будут интересны эти курсы:

Оставьте свой комментарий

Школьников не планируют переводить на удаленку после каникул

В школе в Пермском крае произошла стрельба

Минобразования Кузбасса рекомендовало техникумам и школам уйти на каникулы до 7 ноября

Минпросвещения намерено включить проверку иллюстраций в критерии экспертизы учебников

Минцифры предложило разработать «созидательные» компьютерные игры

Минобрнауки утвердило перечень олимпиад для школьников на 2021-2022 учебный год

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Читайте также: В цилиндре под поршнем находится влажный воздух при давлении

Видео:Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

Апофема делит сторону основания пополам. Все ли вы знаете о правильной пирамиде?

Для решения задач на обширную тему «Стереометрия» нужно выучить и разобрать очень много элементов и тонкостей, полностью изучить все свойства фигур, а также не забывать свойства всех фигур, которые включены в курс «Планиметрии».

Среди задач по объемным фигурам очень часто встречается правильная пирамида, чтобы легко решать их, нужно хорошо с ней познакомиться. Пирамида называется правильной, если в ее основании лежит правильный многоугольник, а ее вершина спроецирована в центр основания. Как раз при изучении этого многоугольника вы услышите об апофеме.

Как вы уже поняли, в геометрии понятие апофемы — это широко распространенное явление. Невозможно узнать некоторые измерения пирамиды без знания этого. Само слово «апофема» — это пришедшее к нам из греческого языка явление, и переводится оно как «откладываю».

Видео:11 класс. Геометрия. Объём пирамиды. 28.04.2020.Скачать

Определение

В планиметрии апофема — перпендикуляр (как сам, так и его длина), который проведен к стороне правильного многоугольника из центра. В стереометрии апофема пирамиды — это высота в боковой грани, которая проведена к основанию. Используется только для правильных пирамид. Соответственно, апофема правильной треугольной пирамиды — это высота ее грани, которая представлена равнобедренным треугольником.

Видео:Площадь поверхности призмы. 11 класс.Скачать

Какова роль апофемы

Апофема — это очень важный элемент пирамиды, потому что с ее помощью можно решить огромное количество задач. В частности, боковая поверхность правильной пирамиды равна полупроизведению периметра основания и апофемы грани.

S_бп = (P_осн*h)/2; h — апофема, это ее ключевая роль.

Не путайте с H (высота объемной фигуры в стереометрии).

Также, благодаря знанию апофемы, можно найти площадь грани как равнобедренного треугольника.

Видео:Усеченная пирамида. 11 класс.Скачать

Свойства апофемы

Их мало, но все же их нужно помнить. В целом это следствия, вытекающие из определения. Итак, апофема в правильной пирамиде:

1. Опущена на сторону основания под углом 90 градусов.
2. Делит сторону, на которую опущена, пополам, так как является высотой в равнобедренном/равностороннем треугольнике и по совместительству — медианой.

В правильной пирамиде все апофемы равны, так как все ее боковые грани также одинаковые. При нахождении длины апофемы вам придется воспользоваться как свойствами многоугольника, так и свойствами многогранника. Как же найти числовое значение апофемы в правильной пирамиде?

Видео:🔴 Найдите объём правильной четырёхугольной ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Как найти апофему пирамиды

Ее можно найти, применяя все ранее полученные знания, вот всего лишь несколько примеров:

• Если известны боковое ребро и сторона основания. Так как апофема делит сторону основания пополам и образует с ней угол в 90 градусов, то найти ее из прямоугольного треугольника по теореме Пифагора вам не составит труда. Также можно найти апофему, используя знания соотношений в прямоугольном треугольнике.
• Если известен радиус вписанной окружности в основание правильной пирамиды и высота всей фигуры. Радиус, проведенный к точке касания, перпендикулярен касательной, и апофема перпендикулярна этой стороне основания (которая является касательной к вписанной окружности). Высота фигуры перпендикулярна основанию и попадает в центр окружности, вписанной в основание пирамиды. Следовательно, радиус и высота фигуры являются катетами и образуют прямой угол, а вместе с апофемой — прямоугольный треугольник. И опять же по теореме Пифагора или через соотношения в прямоугольном треугольнике вы легко найдете апофему.

В любом случае при нахождении апофемы вам придется вспоминать все основные законы и правила планиметрии. Если неизвестны какие-то элементы из этого списка, то вы можете оперировать данными параметрами, и, постепенно находя вышеописанные данные, найти апофему вам не составит труда. Надеемся, что наша статья помогла вам в освоении такой интересной темы.

🔍 Видео

Геометрия 11 класс: Объем призмы и цилиндра. ВидеоурокСкачать

Объем пирамиды. Практическая часть. 11 класс.Скачать

Пирамида. 11 класс.Скачать

11 класс. Контрольная №4 (из 6). Тема: Объем призмы, цилиндра и конуса. Решение с советами! :)Скачать

ВСЕ О ПИРАМИДАХ! ЧАСТЬ I #shorts #егэ #огэ #математика #геометрия #пирамидаСкачать

Призма и ее элементы, виды призм. Практическая часть - решение задачи. 11 класс.Скачать