Как найти диаметр основания цилиндра зная площадь боковой поверхности

Видео:Видеоурок по математике "Цилиндр"Скачать

Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников

Курс-тренинг Разбираем вариант 97 (1-14) —> Полный цикл видеоуроков по задачам 1-14 —> Полная В-подготовка (задачи 1-14) Полный цикл видеоуроков по задачам 1-14 При каком условии верно равенство 2990 + 1990 + 990 = 3900? —> Новые курсы: «EGE-мастер», «Достойный балл», «Ларинские варианты», «Раз-в-неделю», «Всё включено» —> Постоянно работают курсы для выпускников, учителей и репетиторов

12(B13). Найти диаметр основания цилиндра, если дана боковая поверхность (вар. 49)

Площадь боковой поверхности цилиндра равна 56π, а высота равна 7. Найдите диаметр основания.

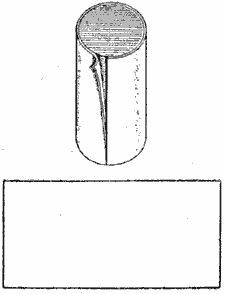
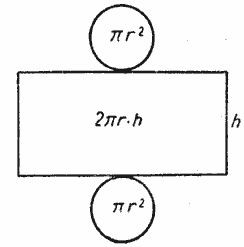
Что представляет из себя боковая поверхность цилиндра? Разрежем его мысленно по образующей. При этом получим обыкновенный прямоугольник. Одно из его измерений — высота цилиндра. Второе измерение — длина окружности основания цилиндра. Она равна 2π·R = π·(2R) = π·D. На рисунке изображена полная развёртка цилиндра, но нас интересует только прямоугольник. Площадь прямоугольника (боковая поверхность) равна (π·D)·Н. По условию она равна 56π. Получаем (π·D)·Н = 56π. Отсюда D·Н = 56. Учтём теперь, что по условию высота равна 7. D·7 = 56. Отсюда находим диаметр D = 8. Ответ: 8 Можно поступить и так. В формулу боковой поверхности цилиндра S_бок. = 2π·R·H подставить площадь 56π и высоту 7, получим 56π = 2πR·7, 56 = 2R·7, 8 = 2R = D.

Автор: Ольга Себедаш Просмотров: 45072

Курс-тренинг Разбираем вариант 97 (1-14) —> Полный цикл видеоуроков по задачам 1-14 —> Полная В-подготовка (задачи 1-14) Полный цикл видеоуроков по задачам 1-14 При каком условии верно равенство 2990 + 1990 + 990 = 3900? —> Новые курсы: «EGE-мастер», «Достойный балл», «Ларинские варианты», «Раз-в-неделю», «Всё включено» —> Постоянно работают курсы для выпускников, учителей и репетиторов

Комментарии к этой задаче:

Комментарий добавил(а): Артур
Дата: 2014-06-03

А общее формула нахождение диаметра цилиндра? Она имеет лишь такое произведение? Или есть иное?

Видео:Цилиндр - расчёт площади, объёма.Скачать

Как посчитать объем цилиндра

Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Онлайн калькулятор

Найти чему равен объем цилиндра (V) можно зная (либо-либо):

• радиус r и высоту h цилиндра
• диаметр d и высоту h цилиндра
• площадь основания S_o и высоту h цилиндра
• площадь боковой поверхности S_b и высоту h цилиндра

Читайте также: Самодельный цилиндр для 2т мотоцикла

Подставьте значения в соответствующие поля и получите результат.

Зная радиус r и высоту h

Чему равен объем цилиндра V если известны его радиус r и высота h?

Формула

Пример

Если цилиндр имеет высоту h = 8 см, а его радиус r = 2 см, то:

V = 3.14156 ⋅ 2 2 ⋅ 8 = 3.14156 ⋅ 32 = 100.53 см 3

Зная диаметр d и высоту h

Чему равен объем цилиндра V если известны его диаметр d и высота h?

Формула

Пример

Если цилиндр имеет высоту h = 5 см, а его диаметр d = 1 см, то:

V = 3.14156 ⋅ ( 1 /₂) 2 ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см 3

Зная площадь основания S_o и высоту h

Чему равен объем цилиндра V если известны его площадь основания S_o и высота h?

Формула

Пример

Если цилиндр имеет высоту h = 10 см, а площадь его основания S_o = 5 см 2 , то:

Зная площадь боковой поверхности S_b и высоту h

Чему равен объем цилиндра V если известны его площадь боковой поверхности S_b и высота h?

Формула

Пример

Если цилиндр имеет высоту h = 5 см, а площадь его боковой поверхности S_b = 30 см 2 , то:

V = 30 2 / _{4 ⋅ 3.14⋅ 5} = 900 /_62.8 = 14.33 см 3

Видео:60. Площадь поверхности цилиндраСкачать

Нахождение площади поверхности цилиндра: формула и задачи

В данной публикации мы рассмотрим, как можно найти площадь поверхности цилиндра и разберем примеры решения задач для закрепления материала.

Видео:№537. Диаметр основания цилиндра равен 1 м, высота цилиндра равна длинеСкачать

Формула вычисления площади цилиндра

1. Боковая поверхность

Площадь (S) боковой поверхности цилиндра равна произведению длины окружности, являющейся основанием фигуры, на его высоту.

Длина окружности, в свою очередь, рассчитывается так: C = 2 π R. Следовательно, рассчитать площадь можно следующим образом:

Примечание: в вычислениях значение числа π округляется до 3,14.

2. Основание

В качестве оснований цилиндра (равны между собой), выступает круг, площадь которого равна:

Т.к. диаметр круга равен двум его радиусам (d = 2R), выражение можно преобразовать таким образом:

3. Полная площадь

Для нахождения данной величины необходимо просуммировать площади боковой поверхности и двух равных оснований цилиндра, т.е.:

S = 2 π R h + 2 π R 2 или S = 2 π R (h + R)

Видео:№538. Площадь боковой поверхности цилиндра равна 5. Найдите площадь осевогоСкачать

Примеры задач

Задание 1
Найдите площадь боковой поверхности цилиндра, если его радиус равен 11 см, а высота – 8 см.

Решение:
Воспользуемся первой формулой, подставив в нее данные по условиям задачи значения:
S = 2 ⋅ 3,14 ⋅ 11 см ⋅ 8 см = 552,64 см 2 .

Задание 2
Высота цилиндра равна 9 см, а его диаметр – 8 см. Найдите суммарную площадь поверхности фигуры.

Решение:
Если диаметр цилиндра равен 8 см, значит его радиус составляет 4 см (8 см / 2). Применив соответствующую формулу для нахождения площади получаем:
S = 2 ⋅ 3,14 ⋅ 4 см ⋅ (9 см + 4 см) = 326,56 см 2 .

Видео:Геометрия Задача про монаха Найти диаметр цилиндраСкачать

Нахождение радиуса цилиндра: формула и примеры

В данной публикации мы рассмотрим, как можно вычислить радиус цилиндра и разберем примеры решения задач для закрепления материала.

Видео:Нахождение площади боковой поверхности цилиндраСкачать

Формулы вычисления радиуса цилиндра

1. Через объем и высоту

Радиус цилиндра рассчитывается по формуле:

V – объем цилиндра; считается как произведение числа π на высоту фигуры на квадрат радиуса круга, являющего ее основанием.

• R – радиус основания цилиндра, т.е. окружности;
• π – число, округленное значение которого равняется 3,14.

2. Через площадь боковой поверхности

Радиус цилиндра считается таким образом:

S_бок. – площадь боковой поверхности цилиндра; равна произведению длины окружности (2 π R), являющейся основанием фигуры, на его высоту:

3. Через полную площадь поверхности

Данная формула получена следующим образом:

S – полная площадь поверхности фигуры, равная:

Читайте также: Шлифовка плоскости блока цилиндров своими руками

S = 2 π Rh + 2 π R 2 или S = 2 π R(h + R)

Возьмем первое выражение. Если перенести S в правую часть, получим:

2 π R 2 + 2 π Rh – S = 0

Можно заметить, что это квадратное уравнение вида ax 2 + bx + c = 0, где:

R является корнем данного уравнения (x). Подставив в стандартную формулу для расчета корней наши значения a, b и с получаем*:

* в нашем случае – только один положительный корень, т.к. радиус не может быть отрицательным.

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Примеры задач

Задание 1
Высота цилиндра равняется 5 см, а объем – 141,3 см 3 . Вычислите его радиус.

Решение:
Воспользуемся соответствующей формулой, подставив в нее известные по условиям задачи значения:

Задание 2
Найдите радиус цилиндра, если площадь его боковой поверхности равна 175,84 см 2 , а высота составляет 7 см.

Решение:
Применим формулу, в которой задействованы заданные величины:

Задание 3
Рассчитайте радиус цилиндра, если полная площадь его поверхности – 602,88 см 2 , а высота – 10 см.

Решение:
Используем третью формулу для нахождения неизвестной величины:

Видео:Задача на вычисление высоты цилиндраСкачать

Как посчитать объем цилиндра

Видео:Площадь полной поверхности цилиндраСкачать

Онлайн калькулятор

Найти чему равен объем цилиндра (V) можно зная (либо-либо):

• радиус r и высоту h цилиндра
• диаметр d и высоту h цилиндра
• площадь основания S_o и высоту h цилиндра
• площадь боковой поверхности S_b и высоту h цилиндра

Подставьте значения в соответствующие поля и получите результат.

Зная радиус r и высоту h

Чему равен объем цилиндра V если известны его радиус r и высота h?

Формула

Пример

Если цилиндр имеет высоту h = 8 см, а его радиус r = 2 см, то:

V = 3.14156 ⋅ 2 2 ⋅ 8 = 3.14156 ⋅ 32 = 100.53 см 3

Зная диаметр d и высоту h

Чему равен объем цилиндра V если известны его диаметр d и высота h?

Формула

Пример

Если цилиндр имеет высоту h = 5 см, а его диаметр d = 1 см, то:

V = 3.14156 ⋅ ( 1 /₂) 2 ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см 3

Зная площадь основания S_o и высоту h

Чему равен объем цилиндра V если известны его площадь основания S_o и высота h?

Формула

Пример

Если цилиндр имеет высоту h = 10 см, а площадь его основания S_o = 5 см 2 , то:

Зная площадь боковой поверхности S_b и высоту h

Чему равен объем цилиндра V если известны его площадь боковой поверхности S_b и высота h?

Формула

Пример

Если цилиндр имеет высоту h = 5 см, а площадь его боковой поверхности S_b = 30 см 2 , то:

V = 30 2 / _{4 ⋅ 3.14⋅ 5} = 900 /_62.8 = 14.33 см 3

Видео:Площадь поверхности призмы. 11 класс.Скачать

Как найти высоту цилиндра, с помощью данных?

Видео:ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ ЦИЛИНДРАСкачать

Объем цилиндра формула (через радиус основания и высоту)

r — радиус основания цилиндра,

Если внимательно посмотреть на эту формулу, то можно заметить, что

— это формула площади круга, а в нашем случае — площадь основания. Поэтому формулу объема цилиндра можно записать через площадь основания и высоту:

Видео:Цилиндр, конус, шар, 6 классСкачать

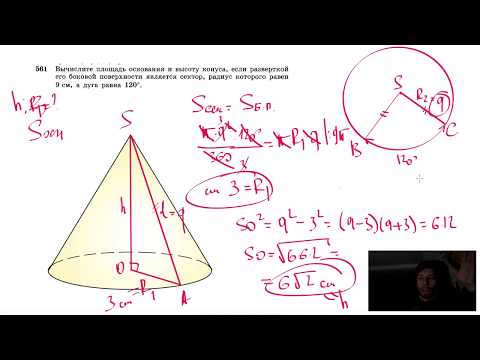
S (б.п.) = hP = 2πrh

— Если известна площадь бок. поверхности S (б.п.) и высота h цилиндра, радиус будет равен частному от деления S (б.п.) на произведение 2пи на высоту:

Видео:#136. Задание 8: цилиндрСкачать

Формула вычисления объема цилиндра

1. Через площадь основания и высоту

Объем (V) цилиндра равняется произведению его высоты и площади основания.

2. Через радиус основания и высоту

Как мы знаем, в качестве оснований цилиндра (равны между собой) выступает круг, площадь которого вычисляется так: S = π ⋅ R 2 . Следовательно, формулу для вычисления объема цилиндра можно представить в виде:

V = π ⋅ R 2 ⋅ H

Примечание: в расчетах значение числа π округляется до 3,14.

3. Через диаметр основания и высоту

Как нам известно, диаметр круга равняется двум его радиусам: d = 2R. А значит, вычислить объем цилиндра можно следующим образом:

Читайте также: Отказ от зажигания цилиндров

V = π ⋅ (d/2) 2 ⋅ H

Нет сомнений, что все мы со школьных лет помним, как найти высоту цилиндра, формула выглядит так: H=V/πR^2 или 4V/D^2.

Расшифровать формулу просто:

• V – объем цилиндра;
• π – 3,14;
• R – радиус цилиндра;
• D – диаметр.

То есть получается, что, если разделить объем на площадь основания, получится высота цилиндра.

Можно поступить проще. Для этого нам придется вычислить площадь боковой поверхности искомого цилиндра. Это легко сделать по формуле: S=2πRH. Слегка изменив формулу, получаем: H=S/2πR.

Таким образом, есть уже два способа, которые помогли вспомнить, как найти высоту цилиндра. Это нетрудно, когда перед глазами стройные формулы.

Видео:ЗАДАЧА 769. МАТЕМАТИКА 6 класс. Площадь боковой поверхности цилиндра. ПРОЕКТ Домашнее обучение.Скачать

Способ расчета радиуса цилиндра:

Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
где V – объем цилиндра, h – высота

Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
где Sb – площадь боковой поверхности, h – высота

Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
где S – площадь полной поверхности, h – высота

S (п.п.) = S (б.п.) + 2S (осн.) = 2πrh + πr2=πr (2h+r)

Площадь боковой поверхности равняется длине окружности основания умноженной на высоту:

R = √V / πh

где V — объем цилиндра, h — высота.
Полная площадь поверхности цилиндра складывается из сумм площадей его боковой поверхности и двух оснований:

Видео:№561. Вычислите площадь основания и высоту конуса, если разверткой его боковой поверхностиСкачать

Примеры задач

Задание 1
Высота цилиндра равняется 5 см, а объем – 141,3 см 3 . Вычислите его радиус.

Решение:
Воспользуемся соответствующей формулой, подставив в нее известные по условиям задачи значения:

Задание 2
Найдите радиус цилиндра, если площадь его боковой поверхности равна 175,84 см 2 , а высота составляет 7 см.

Решение:
Применим формулу, в которой задействованы заданные величины:

Задание 3
Рассчитайте радиус цилиндра, если полная площадь его поверхности – 602,88 см 2 , а высота – 10 см.

Решение:
Используем третью формулу для нахождения неизвестной величины:

Видео:РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать

Через площадь боковой поверхности

Радиус цилиндра считается таким образом:

S_бок. – площадь боковой поверхности цилиндра; равна произведению длины окружности (2 π R), являющейся основанием фигуры, на его высоту:

Видео:11 класс, 17 урок, Площадь поверхности конусаСкачать

Площадь полной поверхности цилиндра через радиус основания и высоту

Формула для нахождения полной поверхности цилиндра через высоту и радиус основания:

, где π — число Пи (3,14159…), r — радиус основания цилиндра, h — высота цилиндра.

📽️ Видео

ГЕОМЕТРИЯ 11 класс: Цилиндр. Площадь поверхностиСкачать