Как найти момент силы цилиндра

В динамике поступательного движения материальной точки кроме кинематических характеристик вводились понятия силы и массы. При изучении динамики вращательного движения вводятся физические вели­чины — момент сил и момент инерции, физический смысл которых рас­кроем ниже.

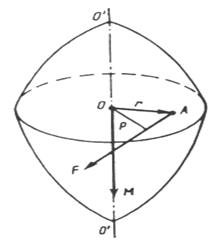
Пусть некоторое тело под действием силы , приложенной в точке А, приходит во вращение вокруг оси ОО’ (рисунок 5.1).

Рисунок 5.1 – К выводу понятия момента силы

Сила действует в плоскости, перпендикулярной оси. Перпендикуляр р, опущенный из точки О (лежащей на оси) на направление силы, назы­вают плечом силы. Произведение силы на плечо определяет модуль мо­мента силы относительно точки О:

Момент силы есть вектор, определяемый векторным произведением радиуса-вектора точки приложения силы и вектора силы:

Единица момента силы — ньютон-метр (Н . м). Направление вектора момента силы находиться с помощью пра­вила правого винта.

Мерой инертности тел при поступательном движении является масса. Инертность тел при вращательном движении зависит не только от массы, но и от ее распределения в пространстве относительно оси вращения. Мерой инертности при вращательном движении служит величина, назы­ваемая моментом инерции тела относительно оси вращения.

Момент инерции материальной точки относительно оси враще­ния — произведение массы этой точки на квадрат расстояния от оси:

Момент инерции тела относительно оси вращения — сумма мо­ментов инерции материальных точек, из которых состоит это тело:

В общем случае, если тело сплошное и представляет собой совокуп­ность точек с малыми массами dm, момент инерции определяется интег­рированием:

где r — расстояние от оси вращения до элемента массой dm.

Если тело однородно и его плотность ρ = m/V, то момент инерции тела

Момент инерции тела зависит от того, относительно какой оси оно вращается и как распределена масса тела по объему.

Наиболее просто определяется момент инерции тел, имеющих пра­вильную геометрическую форму и равномерное распределение массы по объему.

Момент инерции однородного стержня относительно оси, прохо­дящей через центр инерции и перпендикулярной стержню,

Момент инерции однородного цилиндра относительно оси, перпен­дикулярной его основанию и проходящей через центр инерции,

Момент инерции тонкостенного цилиндра или обруча относи­тельно оси, перпендикулярной плоскости его основания и проходящей через его центр,

Момент инерции шара относительно диаметра

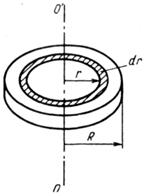
Определим момент инерции диска относительно оси, проходящей че­рез центр инерции и перпендикулярной плоско­сти вращения. Пусть масса диска – m, а его радиус – R.

Площадь кольца (рисунок 5.2), заключенного между r и , равна .

Рисунок 5.2 – К выводу момента инерции диска

Площадь диска . При постоянной толщине кольца,

Тогда момент инерции диска,

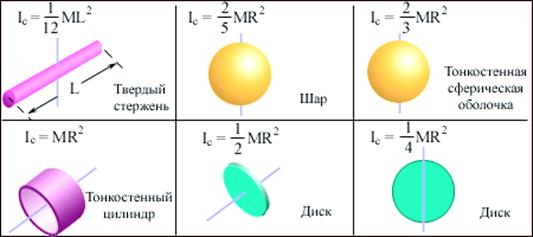
Для наглядности на рисунке 5.3 изображены однородные твердые тела различной формы и указаны моменты инерции этих тел относительно оси, проходящей через центр масс.

Читайте также: Ремкомплект для тормозные цилиндры для заз 968м

Рисунок 5.3 – Моменты инерции I_C некоторых однородных твердых тел.

Теорема Штейнера

Приведенные выше формулы для моментов инерции тел даны при усло­вии, что ось вращения проходит через центр инерции. Чтобы определить моменты инерции тела относительно произвольной оси, следует восполь­зоваться теоремой Штейнера: момент инерции тела относительно произвольной оси вращения равен сумме момента инерции J₀ отно­сительно оси, параллельной данной и проходящей через центр инер­ции тела, и величины md 2 :

где m — масса тела, d — расстояние от центра масс до выбранной оси вра­щения. Единица момента инерции — килограмм-метр в квадрате (кг . м 2 ).

Так, момент инерции однородного стержня длиной l относительно оси, про­ходящей через его конец, по теореме Штейнера равен

Дата добавления: 2017-01-08 ; просмотров: 29728 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Урок 80 (осн). Момент силы. Правило моментовСкачать

Момент инерции цилиндра сплошного и полого: разное положение осей вращения

Знание момента инерции тела позволяет воспользоваться законом сохранения момента импульса либо выражением для описания кругового движения с угловым ускорением. В данной статье рассмотрим, как находить для цилиндра момент инерции при различном положении осей вращения.

Видео:Момент силы. Определение, размерность и знаки. Плечо силыСкачать

Момент инерции: математическое определение

Осевой момент инерции вводится в физику благодаря изучению законов вращательного движения тел. Для точки материальной с массой m, вращающейся на расстоянии r от оси, момент инерции будет равен:

В общем же случае для тела, которое имеет произвольное распределение вещества в пространстве (любую геометрическую форму), величину I можно вычислить так:

По сути, это выражение является обобщением предыдущего. В нем производится суммирование (интегрирование) моментов от каждой элементарной частицы dm, дистанция до оси от которой равна r.

Если говорить о физическом значении рассматриваемой величины I, то она показывает, насколько «сильно» система сопротивляется воздействию внешнего момента силы, который пытается ее раскрутить или, наоборот, остановить.

Видео:Момент силыСкачать

Момент инерции цилиндра относительно оси, его основаниям перпендикулярной

Из приведенной выше формулы можно понять, что величина I является характеристикой всей вращающейся системы, то есть она зависит как от формы тела и распределения в нем массы, так и от относительного положения оси.

В данном пункте рассмотрим простой случай: определить необходимо момент инерции для сплошного цилиндра, ось вращения которого перпендикулярна его основаниям и проходит через гравитационный центр фигуры.

Для решения проблемы применим интегральную формулу для I. В процессе операции интегрирования мысленно разобьем цилиндр на тонкие колечки толщиной dr. Каждое колечко будет иметь объем: dV = 2*pi*r*dr*h, здесь h — высота фигуры. Учитывая, что dm = ρ*dV, где ρ — плотность цилиндра, получаем:

I = ∫r 2 dm = ρ*∫r 2 dV = 2*pi*ρ*h*∫r 3 dr

Этот интеграл необходимо вычислить для пределов от 0 до R, где R — радиус фигуры. Тогда получим:

I = 2*pi*ρ*h*∫ R ₀r 3 dr = 2*pi*ρ*h/4*(r 4 )∣ R ₀ = pi*ρ*h*R 4 /2

Воспользовавшись формулой для массы цилиндра через его объем и плотность, приходим к конечному выражению:

Мы получили формулу инерции момента цилиндра однородного. Она показывает, что величина I для этой фигуры в 2 раза меньше, чем для материальной точки аналогичной массы, которая вращается на расстоянии радиуса цилиндра от оси.

Видео:РЫЧАГ МОМЕНТ СИЛЫ физика 7 класс ПерышкинСкачать

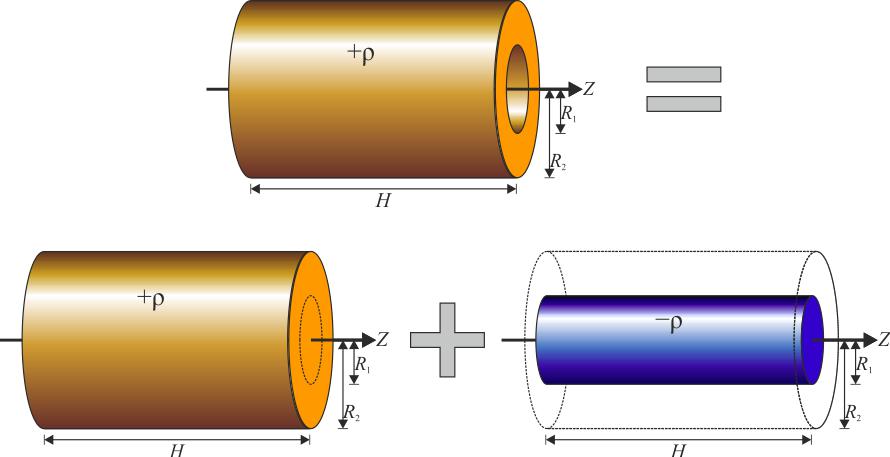
Момент инерции полого цилиндра

Теперь оставим ось на том же месте и найдем значение I для цилиндра с пустотой внутри (втулка, труба). Такую фигуру описывают двумя радиусами: внешним R₁ и внутренним R₂. В этом случае для интегрирования применяется абсолютно тот же подход, что и для сплошного цилиндра, только пределы теперь изменяются от R₂ до R₁. Имеем:

Читайте также: Размеры приспособления для вдавливания заднего тормозного цилиндра golf 6

Для дальнейшего упрощения этой формулы воспользуемся разложением на множители выражения в скобках, получим:

Часть этого выражения вместе с первыми скобками является массой полого цилиндра, поэтому получаем конечную формулу:

Отсюда видно, что момент инерции полого цилиндра больше этого значения для сплошного цилиндра аналогичной массы и такого же внешнего радиуса на величину m*R₂ 2 /2. Этот результат не вызывает удивления, поскольку в полом цилиндре центр масс находится от оси вращения дальше, чем в сплошном.

Видео:Момент силы относительно точки и осиСкачать

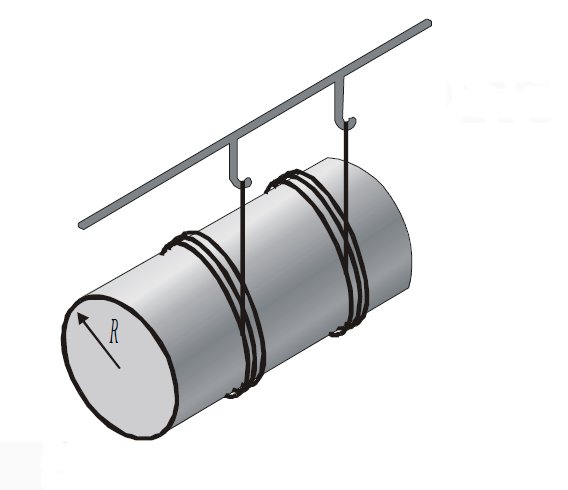
Величина I для цилиндра, ось вращения которого проходит параллельно плоскостям его основания

В такой системе ось вращения проходит также через центр массы цилиндра, но теперь он лежит как бы на боку (на цилиндрической поверхности, см. рис. ниже).

Расчет для момента инерции цилиндра для такой ситуации является непростой задачей, поскольку требует наличия дополнительных знаний для ее решения. Тем не менее приведем необходимые математические выкладки, чтобы читатели имели более полное представление о проведении интегрирования при вычислении I.

Начинаем решать задачу. Разбиваем сплошной цилиндр на отдельные диски бесконечно малой толщины. Чтобы узнать, каким моментом инерции обладает этот диск относительно оси, которая проходит через него и параллельна его основаниям, необходимо выполнить отдельное интегрирование. Оно дает следующий результат:

Чтобы найти, величину I_i для этого диска относительно уже новой оси, которая рассматривается в задаче, необходимо воспользоваться теоремой Штейнера. Получим:

I_i = R 2 *dm/4 + L 2 *dm, здесь L — расстояние от оси до тонкого диска.

Зная, что dm = pi*R 2 *dL*ρ, подставляем в интегральную формулу для I и проводим интегрирование по пределам (-L₀/2; +L₀/2), имеем:

I = ∫_mI_i = ∫_m(R 2 *dm/4 + L 2 *dm) = pi*R 2 *ρ*∫ L0/2 _-L0/2(R 2 *dL/4 + L 2 *dL)

Решение этого интеграла приводит к конечной формуле:

Видео:Урок 94. Вычисление моментов инерции телСкачать

Пример решения задачи

Решим интересную задачу на нахождение осевого момента инерции цилиндра. Пусть он лежит на цилиндрической поверхности, а ось вращения расположена параллельно его основанию и проходит через конец фигуры.

Эта ситуация полностью аналогична рассмотренной в предыдущем пункте, только ось пересекает не гравитационный центр цилиндра, а конец этой фигуры. Тем не менее для решения проблемы можно воспользоваться результатом предыдущего пункта статьи. Применим вышеупомянутую теорему Штейнера, получим:

I = m*R 2 /4 + m*L₀ 2 /12 + m*(L₀/2) 2 = m*R 2 /4 + m*L₀ 2 /3

Этот момент инерции соответствует стержню с осью вращения на его конце.

Видео:Момент инерцииСкачать

Момент инерции для чайников: определение, формулы, примеры решения задач

Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Видео:Момент силыСкачать

Что такое инерция

Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.

Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».

Читайте также: Устройство крышки цилиндра двухтактного двигателя с прямоточно клапанной продувкой

Видео:Момент инерции абсолютно твердого тела. 10 класс.Скачать

Определение момента инерции

Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.

По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.

Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.

Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.

Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:

Видео:Момент силы: почему его так назвали ?Скачать

Теорема Штейнера

От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.

Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Теорема Гюйгенса-Штейнера гласит:

Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.

Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:

Видео:Расчет момента инерции цилиндраСкачать

Пример решения задачи на нахождение момента инерции

Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.

Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.

Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:

Массу кольца можно представить в виде:

Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:

В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.

Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.

Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:

Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.

Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.

🎬 Видео

Урок 78 (осн). Простые механизмы. Рычаг. Условие равновесия рычагаСкачать

Как найти момент силы на ЕГЭ по физике?Скачать

Момент силы относительно точкиСкачать

Как быстро рассчитать момент затяжки болтаСкачать

Скатывание цилиндров с наклонной плоскостиСкачать

Момент импульса и момент силы относительно точки и оси | Студенты, абитуриенты МФТИ | Вуз. физика #1Скачать

Крутящий момент и лошадиные силы | Science Garage На РусскомСкачать

Расчёт момента инерции тела относительно оси вращения. Момент инерции однородного стержняСкачать

Моменты силы, импульса, инерции. Динамика вращательного движенияСкачать