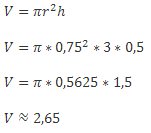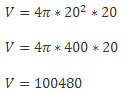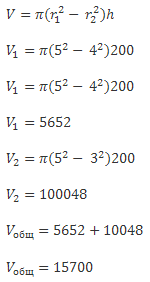Как найти объект цилиндра (3 видео)

Объем цилиндра, формулы и калькулятор для вычисления объема цилиндра и площади его поверхностей, а также необходимая теория о характеристиках цилиндра.

Содержание

Объем правильного цилиндра через радиус и высоту цилиндра
Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра
Формулы и калькулятор для вычисления объема цилиндра через диаметр основания
Объем цилиндрической полости
Поверхности цилиндра
Сечения цилиндра
Что такое объем
Геометрические тела. Цилиндр.
Формулы нахождения элементов цилиндра.
Объем цилиндра — формулы и примеры расчетов
Как найти объем цилиндра
Формула объема цилиндра через диаметр
Объем полого цилиндра
Примеры задач с решениями
Задача №1
Задача №2
Задача №3
Как найти объект цилиндра
🎬 Видео

Видео:Цилиндр - расчёт площади, объёма.Скачать

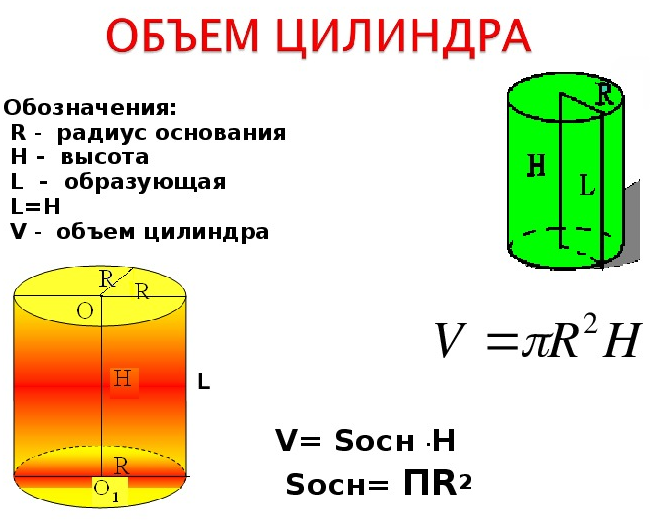
Объем правильного цилиндра через радиус и высоту цилиндра

Видео:Видеоурок по математике "Цилиндр"Скачать

Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра

Видео:Объём цилиндраСкачать

Формулы и калькулятор для вычисления объема цилиндра через диаметр основания

Видео:Как выставить ВМТ любого цилиндра не зная меток и порядка работы цилиндровСкачать

Объем цилиндрической полости

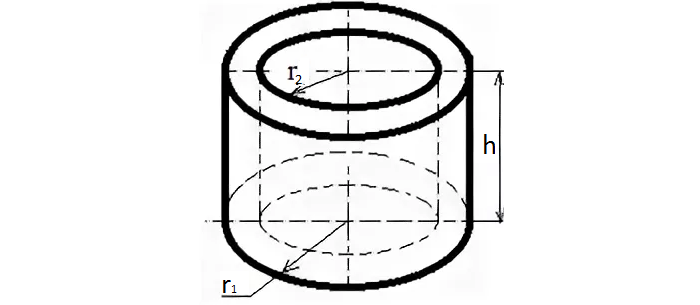
Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.

На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.

Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.

Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.

Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.

Рассмотрим правильный цилиндр.

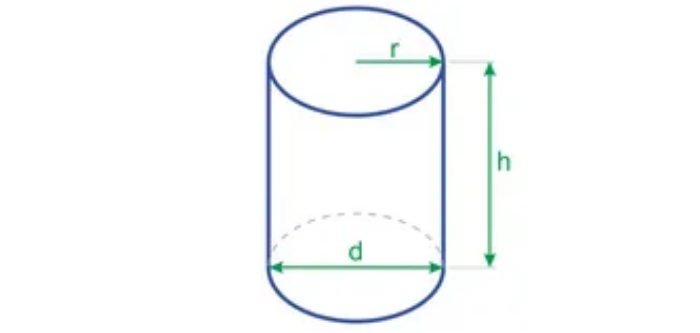
Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник

Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра.

Радиус основания цилиндра, является радиусом цилиндра.

Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.

Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.

Читайте также: Как изготовляют блок цилиндров

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

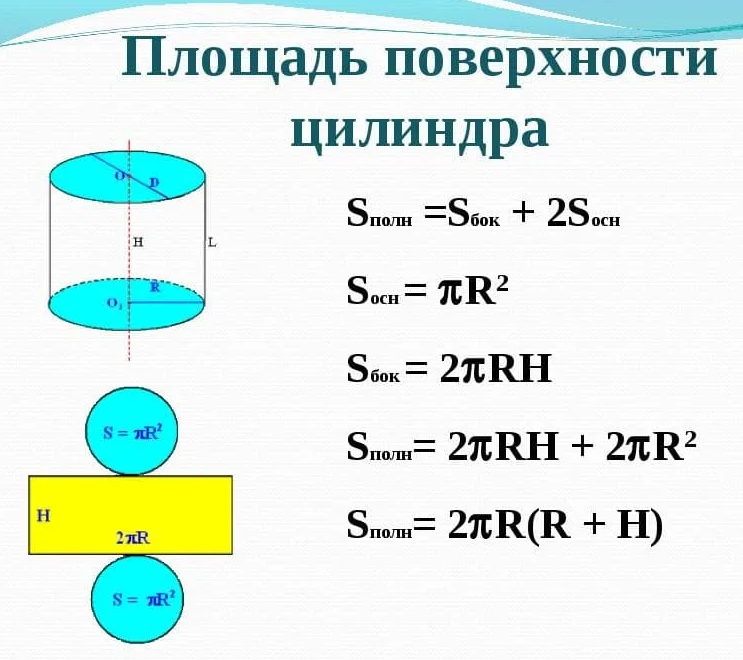
Поверхности цилиндра

Наружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая.

Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой.

Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке).

Видео:11 класс. Геометрия. Объем цилиндраСкачать

Сечения цилиндра

При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура .

При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник , но две боковые стороны которого будут являться кривыми линиями.

Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг .

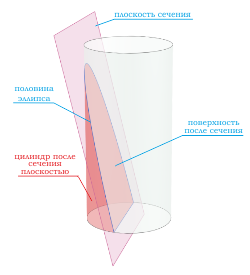
Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс .

Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса .

Видео:Как найти центр круга в мастерской (4 способа)Скачать

Что такое объем

Объем тела (геометрической фигуры) – это количественная характеристика, характеризующая количество пространства, занимаемого телом. Объем выражается в кубических единицах измерения, например: мм 3 , см 3 , мл 3 .

Формула вычисления объема цилиндра часто применяются при расчете массы различных цилиндров, например, прутков, заготовок и т.п. Для вычисления массы, необходимо вычисленный объем цилиндра умножить на плотность материала из которого цилиндр.

Так же, вычислить объём цилиндра иногда требуется для определения полости в виде цилиндра (цилиндрическая полость). В данном случае объём полости будет равен объёму цилиндра, который полностью занимает эту полость.

Объем и площадь других видов цилиндров рассмотрен в статьях:

Видео:Объем цилиндраСкачать

Геометрические тела. Цилиндр.

Цилиндр − это геометрическое тело, которое ограничено цилиндрической поверхностью и 2-мя плоскостями, которые параллельны и пересекают ее.

ABCDEFG и abcdefg — это основания цилиндра. Расстояние между основаниями (KM) – высота цилиндра.

Цилиндрические сечения боковой поверхности кругового цилиндра.

Сечения, которые идут параллельно к основанию, будут являться кругами одного радиуса. Сечения, которые параллельны образующим цилиндра — это пары параллельных прямых (AB || CD). Сечения, не параллельные ни основанию, ни образующим, являются эллипсами.

Цилиндрическая поверхность образуется посредством движения прямой параллельно самой себе. Точка прямой, которая выделена, перемещается вдоль заданной плоской кривой – направляющей. Эта прямая называется образующей цилиндрической поверхности.

Прямой цилиндр – это такой цилиндр, в котором образующие перпендикулярны основанию. Если образующие цилиндра не перпендикулярны основанию, то это будет наклонный цилиндр.

Круговой цилиндр – цилиндр, основанием которого является круг.

Круглый цилиндр – такой цилиндр, который одновременно и прямой, и круговой.

Прямой круговой цилиндр определяется радиусом основания R и образующей L, которая равна высоте цилиндра H.

Призма – это частный случай цилиндра.

Видео:Нумерация цилиндров, как определить где какой номер цилиндра?/how to determine cylinder number?Скачать

Формулы нахождения элементов цилиндра.

Площадь боковой поверхности прямого кругового цилиндра:

Площадь полной поверхности прямого кругового цилиндра:

Объем прямого кругового цилиндра:

Прямой круговой цилиндр со скошенным основанием либо кратко скошенный цилиндр определяют с помощью радиуса основания R, минимальной высоты h₁ и максимальной высоты h₂.

Площадь боковой поверхности скошенного цилиндра:

Площадь оснований скошенного цилиндра:

Площадь полной поверхности скошенного цилиндра:

Объем скошенного цилиндра:

S_бок — площадь боковой поверхности;

Видео:ЕГЭ. Досрок 24 год. Профильный Уровень. Разбор первой частиСкачать

Объем цилиндра — формулы и примеры расчетов

Как найти объем цилиндра? Любой грамотный человек обязан отличить радиус от диаметра, знать, что такое высота, помнить основные формулы геометрии и уметь рассчитать объем шара или куба.

Практическое использование геометрических формул в повседневной жизни очень высоко. Рассчитать объем в кубических метрах перевозимого груза транспортной компанией, пропускную способность трубы под домом и многое другое — во всех этих и подобных им случаях поможет геометрия.

Видео:Как найти ВМТ 1-го цилиндра. Самый точный метод для того чтобы найти верхнюю мертвую точку.Скачать

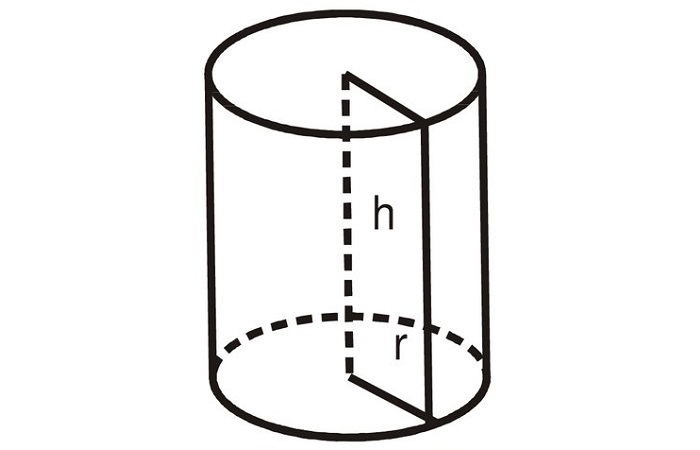
Как найти объем цилиндра

При упоминании о цилиндре на ум приходит классический головной убор. Кроме него в окружении можно встретить много разновидностей этой фигуры.

В теории — это тело, которое ограничено цилиндрической поверхностью и пересекающими её параллельными плоскостями.

Рассчитать его объем возможно следующим образом:

Как видите, формула проста и прозрачна, и если обывателю нужно, как вариант, определить объем цистерны воды, можно смело ее использовать. Хотя, если возникают сомнения в правильности расчетов, для этой цели можно использовать калькулятор и определить объем онлайн.

Видео:Как правильно найти ВМТ первого цилиндра перед установкой зажигания на тракторе Т 25Скачать

Формула объема цилиндра через диаметр

К сожалению, случается, что при расчете объема фигуры известны не все размеры. Так, например, может не быть данных о радиусе.

В данном случае, если знать диаметр или иметь возможность его измерить, можно воспользоваться следующей формулой:

Видео:Как начертить цилиндр в объемеСкачать

Объем полого цилиндра

Расчет полого цилиндра нужен, когда необходимо, например, рассчитать вес полой трубы. Ее масса равна произведению плотности материала и объема.

Видео:Как правильно найти первый цилиндр для установки зажигания Т 40, МТЗ 80.Скачать

Примеры задач с решениями

Задача №1

Высота бочки с водой равна 3 метрам, радиус составляет 0,75 метра. Рассчитать в литрах, сколько нужно жидкости, чтобы заполнить емкость наполовину?

Задача №2

В цехе подготовили заготовку цилиндра. Диаметр основания равен высоте и составляет 20 см. Нужно найти объем заготовки.

Задача №3

На производстве нужно изготовить две трубы с двумя равными поверхностями. Внешний радиус первой трубы равен 5см, а внутренний 4 см, высота 200 см. Внутренний радиус второй равен 3 см.

Сколько понадобится материала для изготовления труб?

Видео:Проекции точек на поверхности цилиндра. Урок 36.(Часть2.ПРОЕКЦИОННОЕ ЧЕРЧЕНИЕ)Скачать