Как найти объем параллелепипеда если в него вписан цилиндр

Видео:ЕГЭ СТЕРЕОМЕТРИЯ КАК НАЙТИ ОБЪЕМ ПАРАЛЛЕЛЕПИПЕДА ВПИСАННОГО В ПУЗАТЫЙ ЦИЛИНДР | МОЩНАЯ ЗАДАЧКАСкачать

Как найти объем параллелепипеда если в него вписан цилиндр

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому площадь основания равна 4, а объем параллелепипеда равен

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 18. Найдите объем параллелепипеда.

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому площадь основания равна 1296, а объем параллелепипеда равен

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 7. Найдите объем параллелепипеда.

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому площадь основания равна 14 2 = 196, а объем параллелепипеда равен

площадь основания круга пr^2,зачем вы диаметр возводите в квадрат ??

Диаметр является стороной квадрата, лежащего в основании параллелепипеда. Диаметр в квадрате — площадь этого основания.

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1,5. Найдите объем параллелепипеда.

Это задание ещё не решено, приводим решение прототипа.

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому площадь основания равна 4, а объем параллелепипеда равен

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 6. Найдите объем параллелепипеда.

Это задание ещё не решено, приводим решение прототипа.

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому площадь основания равна 4, а объем параллелепипеда равен

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 8,5. Найдите объем параллелепипеда.

Это задание ещё не решено, приводим решение прототипа.

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому площадь основания равна 4, а объем параллелепипеда равен

Читайте также: Тормозной цилиндр старого образца урал

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 9,5. Найдите объем параллелепипеда.

Это задание ещё не решено, приводим решение прототипа.

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому площадь основания равна 4, а объем параллелепипеда равен

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 2. Найдите объем параллелепипеда.

Это задание ещё не решено, приводим решение прототипа.

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому площадь основания равна 4, а объем параллелепипеда равен

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 15. Найдите объем параллелепипеда.

Это задание ещё не решено, приводим решение прототипа.

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому площадь основания равна 4, а объем параллелепипеда равен

Видео:КАК НАЙТИ ВЫСОТУ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА, ЕСЛИ ИЗВЕСТЕН ОБЪЕМ, ДЛИНА И ШИРИНА? Пример 5 классСкачать

Как найти объем параллелепипеда если в него вписан цилиндр

Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.

Радиусы шара и основания цилиндра равны. Площадь поверхности цилиндра, с радиусом основания r и высотой 2r равна

Площадь поверхности шара радиуса r равна то есть в 1,5 раза меньше площади поверхности цилиндра. Следовательно, площадь поверхности шара равна 12.

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому площадь основания равна 4, а объем параллелепипеда равен

Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому сторона основания равна 8, а площадь основания равна 64. Тогда высота цилиндра равна

Почему получилось 64? Что-то не понятно:(

Длина диаметра цилиндра равна длине стороны квадрата в основании.

Читайте также: Как вытащить поршни из тормозного цилиндра

В куб вписан шар радиуса 1. Найдите объем куба.

Ребро куба равно диаметру вписанного в него шара, а объем куба равен кубу его ребра. Отсюда имеем:

В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.

По теореме Пифагора длина гипотенузы треугольника в основании Поскольку гипотенуза является диаметром основания описанного цилиндра, его объем

Видео:Математика 5 Объем Объем прямоугольного параллелепипедаСкачать

Как найти объем параллелепипеда если в него вписан цилиндр

Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.

Радиусы шара и основания цилиндра равны. Площадь поверхности цилиндра, с радиусом основания r и высотой 2r равна

Площадь поверхности шара радиуса r равна то есть в 1,5 раза меньше площади поверхности цилиндра. Следовательно, площадь поверхности шара равна 12.

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому площадь основания равна 4, а объем параллелепипеда равен

Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому сторона основания равна 8, а площадь основания равна 64. Тогда высота цилиндра равна

Почему получилось 64? Что-то не понятно:(

Длина диаметра цилиндра равна длине стороны квадрата в основании.

В куб вписан шар радиуса 1. Найдите объем куба.

Ребро куба равно диаметру вписанного в него шара, а объем куба равен кубу его ребра. Отсюда имеем:

В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.

По теореме Пифагора длина гипотенузы треугольника в основании Поскольку гипотенуза является диаметром основания описанного цилиндра, его объем

Видео:КАК НАЙТИ ОБЪЕМ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА? Примеры | МАТЕМАТИКА 5 классСкачать

Как найти объем параллелепипеда если в него вписан цилиндр

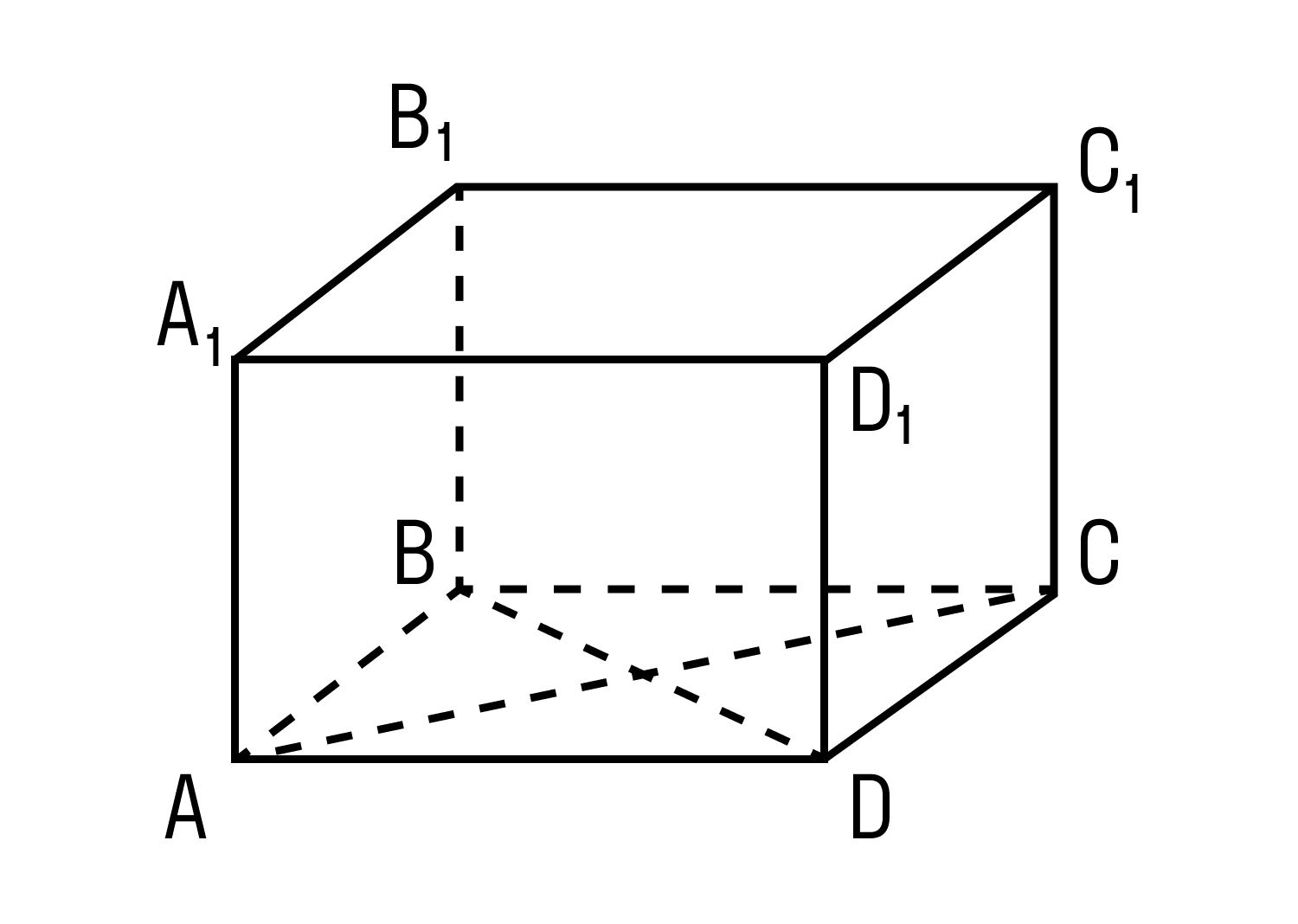
Радиус основания цилиндра равен равен r , а высота равна 5r . Около цилиндра описан параллелепипед, отношение объёма которого к объёму цилиндра равно . Найдите длину отрезка большей диагонали параллелепипеда, лежащего внутри цилиндра.

Решение

Пусть параллелепипед ABCDA 1B 1C 1D 1 описан около цилиндра (рис.1). Тогда параллелепипед – прямой, окружность одного основания цилиндра вписана в основание ABCD параллелепипеда, а окружность второго основания – в основание A 1B 1C 1D 1 . Поскольку в параллелограммы ABCD и A 1B 1C 1D 1 вписаны окружности, эти параллелограммы – ромбы. Если AC и A 1C 1 – большие диагонали этих ромбов, то AC 1 и A 1C – большие диагонали параллелепипеда. Поскольку высоты цилиндра и параллелепипеда равны, площади оснований параллелепипеда и цилиндра относятся как их объемы, а т.к. радиус окружности, вписанной в ромб, равен r , то площадь ромба равна его полупериметру, умноженному на r . Если a – сторона ромба, то
= = ,
откуда находим, что a = r . Пусть окружность с центром O , вписанная в ромб ABCD , касается стороны AB в точке F , а K – середина AB (рис.2). Обозначим OKB = α . Тогда
sin α = = = , cos α = ,

Читайте также: Пропуск зажигания первого цилиндра рено логан

sin OAB = sin = = ,
поэтому
OA = = r , AC = 2OA = 2r ,

tg CAC 1 = = = , cos CAC 1 = .
Рассмотрим плоскость ACC 1A 1 (рис.3). Центры O и O 1 окружностей, вписанных в ромбы ABCD и A 1B 1C 1D 1 , – середины сторон AC и A 1C 1 прямоугольника ACC 1A 1 . Пусть M и N – точки пересечения первой окружности с отрезком AC , а M 1 и N 1 – второй окружности с отрезком A 1C 1 , причём MM 1 || NN 1 . Пусть диагональ AC 1 пересекает отрезки MM 1 и NN 1 в точках P и Q соответственно. Опустим перпендикуляр PH из точки P на NN 1 . Тогда
PQ = = = = 3r.

Ответ

Источники и прецеденты использования

Проект осуществляется при поддержке и .

Видео:КАК НАЙТИ ВЫСОТУ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА, ЕСЛИ ИЗВЕСТЕН ОБЪЕМ И ПЛОЩАДЬ ОСНОВАНИЯ? 5 классСкачать

Объем параллелепипеда

Видео:Формула объёма прямоугольного параллелепипеда (для 3В)Скачать

Понятие объема

Чтобы без труда вычислить объём любой фигуры, нужно разобраться с определениями.

Объём — это количественная характеристика пространства, занимаемого телом или веществом.

Другими словами, это то, сколько места занимает предмет.

Объём измеряется в единицах измерения размера пространства, занимаемого телом, то есть в кубических метрах, кубических сантиметрах, кубических миллиметрах.

За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (см 3 ), кубический миллиметр (1 мм 3 ), кубический метр (1 м 3 ).

Объём всегда выражается в положительных числах. Это число показывает, какое именно количество единиц измерения есть в теле. Например, сколько воды в бассейне, сока в графине, земли в клумбе.

Любое объемное тело имеет объем. Получается, при желании мы можем вычислить объем кружки, смартфона, вазы, кота — чего угодно.

Видео:Параллелепипед описан около цилиндраСкачать

Объем прямоугольного параллелепипеда

Прямоугольный параллелепипед — это многогранник с шестью гранями, каждая из которых является параллелограммом.

Прямоугольным параллелепипедом называют параллелепипед, у которого основание — прямоугольник, а боковые ребра образуют с основаниями прямые углы.

Формула объема прямоугольного параллелепипеда

Чтобы вычислить объем прямоугольного параллелепипеда, найдите произведение его длины, ширины и высоты:

Чтобы не запутаться в формулах, запоминайте табличку с условными обозначениями.

🌟 Видео

5 класс, 21 урок, Объемы. Объем прямоугольного параллелепипедаСкачать

Задачи на цилиндр. Цилиндр и параллелепипед - bezbotvyСкачать

Геометрия Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4Скачать

Цилиндр - расчёт площади, объёма.Скачать

Найти объем параллелепипеда (геометрия от bezbotvy)Скачать

ЗАДАНИЕ 2| ЕГЭ ПРОФИЛЬ| Цилиндр вписан в прямоугольный параллелепипед. Радиус основания и высота цилСкачать

Математика 5 класс (Урок№32 - Объём прямоугольного параллелепипеда. Единицы объёма.)Скачать

КАК НАЙТИ ПЛОЩАДЬ ПОВЕРХНОСТИ ПРЯМОУГОЛЬНОГО ПАРАЛЛЕЛЕПИПЕДА? Примеры | МАТЕМАТИКА 5 классСкачать

Задание 2 ЕГЭ профиль (Стереометрия) по сборнику Ященко 2023Скачать

Площадь поверхности параллелепипедаСкачать

11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

№187. Найдите диагональ прямоугольного параллелепипеда, если его измерения равны: а) 1, 1, 2;Скачать

10 класс, 24 урок, Прямоугольный параллелепипедСкачать