Как найти объем правильной треугольной призмы описанной около цилиндра (8 видео)

Содержание

Цилиндры, вписанные в призмы. Свойства призмы, описанной около цилиндра
Отношение объемов цилиндра и описанной около него правильной n — угольной призмы
Призмы, вписанные в цилиндры
Призмы, вписанные в цилиндр. Свойства призмы, вписанной в цилиндр
Геометрия. 11 класс
💥 Видео

Видео:Как найти объём правильной треугольной призмыСкачать

Цилиндры, вписанные в призмы. Свойства призмы, описанной около цилиндра

Определение 2. Если цилиндр вписан в призму, то призму называют описанной около цилиндра.

Прежде, чем перейти к вопросу о том, в какую же призму можно вписать цилиндр, докажем следующее свойство призм.

Утверждение 1. Если в основания призмы можно вписать окружности, то отрезок, соединяющий центры вписанных окружностей, будет параллелелен и равен боковому ребру призмы.

Рассуждая аналогичным образом, заключаем, что точка O’ равноудалена от всех прямых, на которых лежат ребра верхнего основания A’₁A’₂, A’₂A’₃, . , A_{n – 1}A_n , а поскольку O’ лежит в плоскости верхнего основания, то точка O’ является центром вписанной в многоугольник A’₁A’₂ . A’_n окружности.

В силу того, что прямые OO’ и A₁A’₁ параллельны по построению, а прямые OA₁ и O’A’ параллельны как линии пересечения двух параллельных плоскостей третьей плоскостью, замечаем, что четырехугольник OO’A₁A’₁ является параллелограммом, откуда вытекает равенство: OO’ = A₁A’₁ .

Теорема. В призму можно вписать цилиндр тогда и только тогда, когда выполнены следующие два условия:

Призма является прямой призмой;
В основания призмы можно вписать окружности.

Доказательство. Докажем сначала, что если в n – угольную призму вписан цилиндр, то оба условия теоремы выполнены.

Действительно, выполнение условия 2 следует непосредственно из определения цилиндра, вписанного в призму. Докажем, что выполняется и условие 1, т.е. докажем, что описанная около цилиндра призма является прямой призмой.

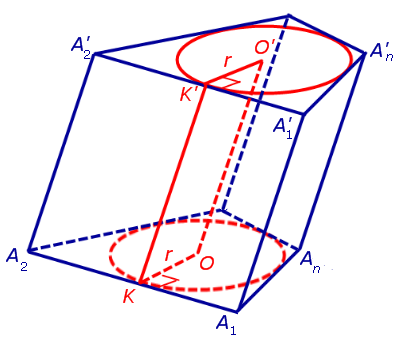
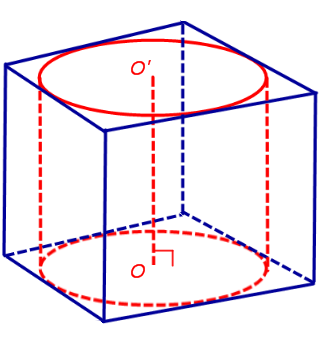
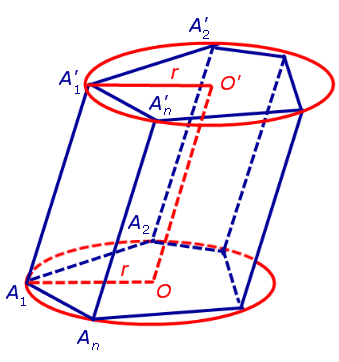
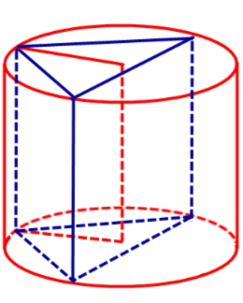
С этой целью рассмотрим ось цилиндра OO’ , соединяющую центры окружностей, вписанных в нижнее и верхнее основания призмы (рис. 3).

Согласно утверждению 1 отрезок OO’ параллелен боковым ребрам призмы. Поскольку ось цилиндра OO’ перпендикулярна к плоскостям его оснований, то и боковые ребра призмы также перпендикулярны к плоскостям оснований, то есть призма является прямой призмой.

Таким образом, мы доказали, что, если призма описана около цилиндра, то оба условия теоремы выполнены.

Теперь рассмотрим прямую n – угольную призму высоты h, в основания которой можно вписать окружности, и докажем, что в такую призму можно вписать цилиндр.

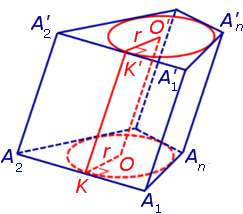
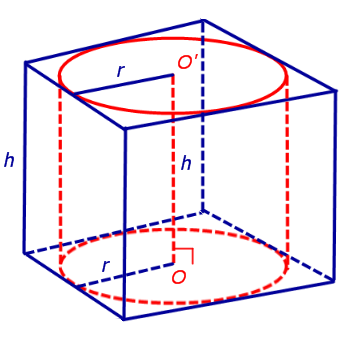
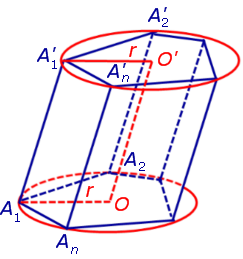
Обозначим буквой O центр окружности радиуса r, вписанной в нижнее основание призмы, а символом O’ обозначим центр окружности, вписанной в верхнее основание призмы (рис. 4).

Поскольку многоугольники, лежащие в основаниях призмы равны, то и радиусы вписанных в них окружностей будут равны. Согласно утверждению 1 отрезок OO’ параллелен и равен боковому ребру призмы. Так как рассматриваемая призма прямая, то ее боковые ребра перпендикулярны плоскости основания и равны высоте призмы h. Значит, и отрезок OO’ перпендикулярен плоскости основания призмы и равен h.

Читайте также: Шаровый цилиндр задней подвески ситроен с5

Цилиндр с осью OO’ , радиусом r и высотой h и будет вписан в исходную призму.

Доказательство теоремы завершено.

Следствие 1 . Высота призмы, описанной около цилиндра, равна высоте цилиндра.

Следствие 2. В любую прямую треугольную призму можно вписать цилиндр.

Справедливость этого утверждения вытекает из того факта, что в любой треугольник можно вписать окружность.

Следствие 3. В любую правильную n – угольную призму можно вписать цилиндр.

Для доказательства этого следствия достаточно заметить, правильная призма является прямой призмой. Основаниями правильной призмы являются правильные многоугольники, а в любой правильный n – угольник можно вписать окружность.

Видео:ЕГЭ. Математика. База . Задача 16. Найдите площадь боковой поверхности правильной треугольной призмыСкачать

Отношение объемов цилиндра и описанной около него правильной n — угольной призмы

Задача. Найти отношение объемов цилиндра и описанной около него правильной n — угольной призмы.

Решение. Поскольку и объем цилиндра, и объем призмы объем призмы вычисляются по формуле

а высота цилиндра равна высоте описанной около него призмы, то для объемов цилиндра и описанной около него правильной n — угольной призмы справедливо равенство

Следствие 4. Отношение объема цилиндра к объему описанной около него правильной треугольной призмы правильной треугольной призмы равно

Следствие 5. Отношение объема цилиндра к объему описанной около него правильной четырехугольной призмы правильной четырехугольной призмы равно

Следствие 6. Отношение объема цилиндра к объему описанной около него правильной шестиугольной призмы равно

Видео:Геометрия Найдите площадь боковой поверхности правильной треугольной призмы, описанной околоСкачать

Призмы, вписанные в цилиндры

Видео:Найти объем правильной треугольной пирамидыСкачать

Призмы, вписанные в цилиндр. Свойства призмы, вписанной в цилиндр

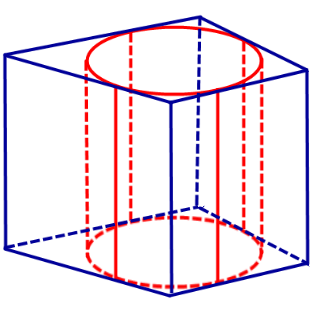
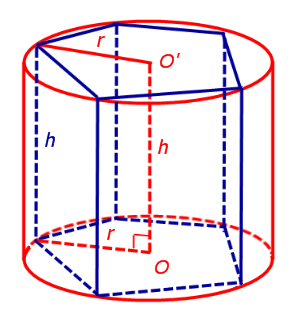
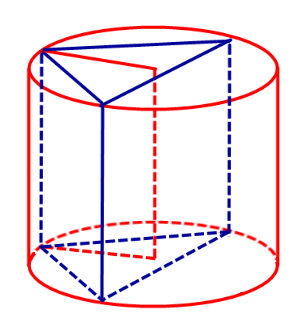
Определение 1. Призмой, вписанной в цилиндр, называют такую призму, основания которой вписаны в окружности оснований цилиндра, а боковые ребра призмы являются образующими цилиндра (рис. 1).

Определение 2. Если призма вписана в цилиндр, то цилиндр называют описанным около призмы.

Прежде, чем перейти к вопросу о том, какую призму можно вписать в цилиндр, докажем следующее свойство призм.

Утверждение 1. Если около оснований призмы можно описать окружности, то отрезок, соединяющий центры описанных окружностей, будет параллелелен и равен боковому ребру призмы.

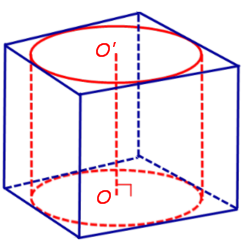
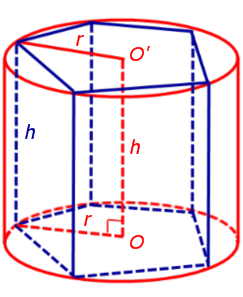
Докажем, что точка O’ является центром окружности радиуса r, описанной около верхнего основания призмы. С этой целью рассмотрим, например, четырехугольник A₁A’₁O’O (рис. 2).

Рассуждая аналогичным образом, заключаем, что

то есть точка O’ – центр окружности радиуса r , описанной около верхнего основания призмы.

В силу того, что четырехугольник OO’A₁A’₁ является параллелограммом, получаем равенство

Теорема. Около призмы можно описать цилиндр тогда и только тогда, когда выполнены следующие два условия:

Призма является прямой призмой;
Около оснований призмы можно описать окружности.

Доказательство. Докажем сначала, что если около n – угольной призмы описан цилиндр, то оба условия теоремы выполнены.

Действительно, выполнение условия 2 следует непосредственно из определения цилиндра, описанного около призмы. Из этого определения также следует, что вписанная в цилиндр призма является прямой призмой, поскольку образующие цилиндра перпендикулярны к плоскостям его оснований,

Читайте также: Гидравлический домкрат с полым цилиндром

Таким образом, мы доказали, что, если призма вписана в цилиндр, то оба условия теоремы выполнены.

Теперь рассмотрим прямую n – угольную призму высоты h, около оснований которой можно описать окружности, и докажем, что около такой призмы можно описать цилиндр.

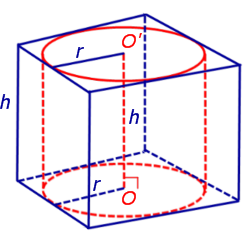
Обозначим буквой O центр окружности радиуса r, описанной около нижнего основания призмы, а символом O’ обозначим центр окружности, описанной около верхнего основания призмы.

Поскольку многоугольники, лежащие в основаниях призмы равны, то и радиусы описанных около них окружностей будут равны. Согласно утверждению 1 отрезок OO’ параллелен и равен боковому ребру призмы. Так как рассматриваемая призма прямая, то ее боковые ребра перпендикулярны плоскости основания и равны высоте призмы h. Значит, и отрезок OO’ перпендикулярен плоскости основания призмы и равен h.

Цилиндр с осью OO’ , радиусом r и высотой h и будет описан около исходной призмы.

Доказательство теоремы завершено.

Следствие 1. Высота призмы, вписанной в цилиндр, равна высоте цилиндра.

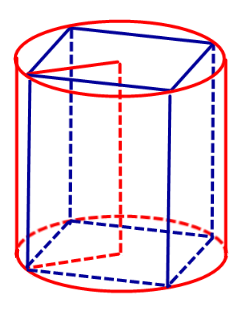
Следствие 2. Около любой прямой треугольной призмы можно описать цилиндр (рис. 4).

Следствие 3. Около любого прямоугольного параллелепипеда (в частности, около куба прямоугольного параллелепипеда (в частности, около куба ) можно описать цилиндр (рис. 5).

Замечание 1. Если у прямоугольного параллелепипеда прямоугольного параллелепипеда три ребра, выходящие из одной вершины, равны a, b, c и различны, то существует три возможности описать около этого параллелепипеда цилиндр в зависимости от того, какое из ребер параллелепипеда выбрано в качестве образующей описанного цилиндра (рис. 6, 7, 8).

Видео:Геометрия Объем правильной треугольной призмы равен 25√3. Радиус окружности, описанной околоСкачать

Геометрия. 11 класс

Конспект урока

Урок №12. Объемы прямой призмы и цилиндра

Перечень вопросов, рассматриваемых в теме

1) Доказательство теорем об объемах прямой призмы и цилиндра

2) Определение призмы, вписанной в цилиндр и призмы описанной около цилиндра

3) Решение задач на нахождение объемов прямой призмы и цилиндра

V=Sh объем прямой призмы и цилиндра

Бутузов В. Ф., Кадомцев С. Б., Атанасян Л. С. и др. Геометрия. 10–11 классы : учеб.для общеобразоват. организаций : базовый и углубл. Уровни – М.: Просвещение, 2014. – 255, сс. 121-126.

Шарыгин И.Ф. Геометрия. 10–11 кл.: учеб.для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 178-196.

Потоскуев Е.В., Звавич Л. И., Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 5-30.

Теоретический материал для самостоятельного изучения

Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.

Прямая призма — это призма, у которой боковые ребра перпендикулярны плоскости основания, откуда следует, что все боковые грани являются прямоугольниками

Читайте также: Потек главный цилиндр сцепления ваз 2107

Объем всякого цилиндра равен произведению площади основания на высоту

Объем призмы — это произведение площади ее основания на высоту

Призма вписана в цилиндр, если ее основания вписаны в основания цилиндра.

Призма описана около цилиндра, если ее основания описаны около оснований цилиндра.

Высота любой призмы (вписанной в цилиндр или описанной около цилиндра), равна высоте самого цилиндра

Примеры и разбор решения заданий тренировочного модуля

№1. Найти объем прямой треугольной призмы высотой 6, в основании которой — прямоугольный треугольник с катетами 3 и 7.

Решение: Объем призмы вычисляется по формуле , т.к. в основании призмы – прямоугольный треугольник, то объем призмы будет вычисляться по формуле , где а и в – катеты треугольника. Подставляя все данные задачи в формулу, получаем ответ: .

№2. Найти объём правильной -угольной призмы, у которой каждое ребро равно а, если: а) n=3, б) n=4, в) n=6.

Решение: поскольку призма правильная, значит, это прямая призма и в основании лежит правильный многоугольник.

Формулу для вычисления объёма прямой призмы мы только что вывели . Поскольку, по условию все ребра призмы равны a, значит, высота призмы равна h=a. Осталось найти площадь основания.

Основанием правильной треугольной призмы является правильный, то есть равносторонний треугольник n=3. Площадь правильного треугольника со стороной f вычислить несложно, она равна .

Применяя формулу для вычисления объёма прямой призмы, получим, что объём правильной треугольной призмы равен .

Основанием правильной четырёхугольной призмы является квадрат n=4. Площадь квадрата со стороной a равна . Тогда объём правильной четырёхугольной призмы равен .

Основанием правильной шестиугольной призмы является правильный шестиугольник n=6. Своими большими диагоналями шестиугольник делится на 6 равносторонних треугольников. Площадь каждого из треугольников равна , значит, площадь правильного шестиугольника равна . Тогда объём правильной шестиугольной призмы равен .

Ответ 3/2 ед 3

№3 Найди объём прямой призмы если =120°, АВ=5 см, ВС=3см и наибольшая из площадей боковых граней равна 35см 2 .

Решение: боковая грань прямой призмы является прямоугольником.

Площадь каждой боковой грани равна произведению высоты призмы на сторону основания.

То есть большая боковая грань содержит большую сторону основания.

По условию =120°, – тупой, а поскольку напротив большей стороны лежит больший угол, то большей стороной основания будет сторона АС. Вычислим длину стороны АС по теореме косинусов.