Как найти объем цилиндра если в него вписан правильный треугольник (3 видео)

В данной публикации мы рассмотрим, как можно найти объем цилиндра и разберем примеры решения задач.

Содержание

Формула вычисления объема цилиндра
Через площадь основания и высоту
Через радиус основания и высоту
Через диаметр основания и высоту
Примеры задач
Как найти объем цилиндра если в него вписан правильный треугольник
Как написать хороший ответ?
Как найти объем цилиндра если в него вписан правильный треугольник
Как найти объем цилиндра если в него вписан правильный треугольник
Задача. Призма, вписанная в цилиндр
Задача. В цилиндр вписана правильная шестиугольная призма
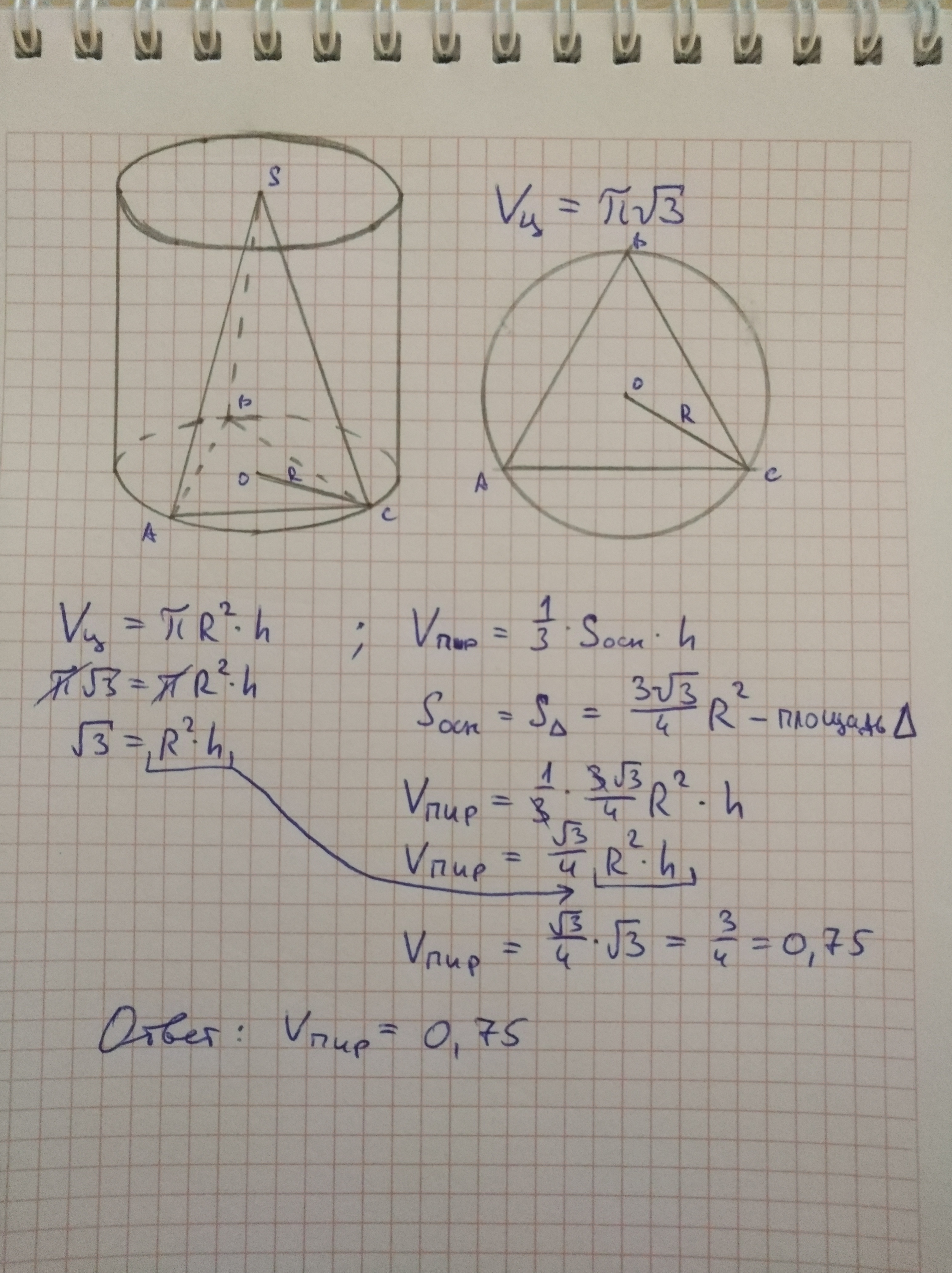
В окружность основания цилиндра вписан правильный треугольник.Найти объем пирамиды той же высоты что и цилиндр,в основании которого лежит этот треугольник,если объем цилиндра равен π√3
Как найти объем цилиндра если в него вписан правильный треугольник
Задача. Призма, вписанная в цилиндр
Задача. В цилиндр вписана правильная шестиугольная призма
🎬 Видео

Видео:Видеоурок по математике "Цилиндр"Скачать

Формула вычисления объема цилиндра

Через площадь основания и высоту

Объем (V) цилиндра равняется произведению его высоты и площади основания.

Через радиус основания и высоту

Как мы знаем, в качестве оснований цилиндра (равны между собой) выступает круг, площадь которого вычисляется так: S = π ⋅ R 2 . Следовательно, формулу для вычисления объема цилиндра можно представить в виде:

V = π ⋅ R 2 ⋅ H

Примечание: в расчетах значение числа π округляется до 3,14.

Через диаметр основания и высоту

Как нам известно, диаметр круга равняется двум его радиусам: d = 2R. А значит, вычислить объем цилиндра можно следующим образом:

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Примеры задач

Задание 1
Найдите объем цилиндра, если дана площадь его основания – 78,5 см 2 , а также, высота – 10 см.

Решение:
Применим первую формулу, подставив в нее известные значения:
V = 78,5 см 2 ⋅ 10 см = 785 см 3 .

Задание 2
Высота цилиндра равна 6 см, а его диаметр – 8 см. Найдите объем фигуры.

Решение:
Воспользовавшись третьей формулой, в которой участвует диаметр, получаем:
V = 3,14 ⋅ (8/2 см) 2 ⋅ 6 см = 301,44 см 3 .

Видео:Геометрия - Построение правильного треугольникаСкачать

Как найти объем цилиндра если в него вписан правильный треугольник

в основание цилиндра вписан правильный треугольник со стороной 3 корня из 3 .Найдите объем цилиндра если его высота равна 5

Ответы и объяснения 1

Применены: формула радиуса окружности, описанной около правильного треугольника, формула объема цилиндра

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и пунктуационных ошибок.

Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
Использовать мат — это неуважительно по отношению к пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Читайте также: Ваз 2112 отказывают цилиндры

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:Задача, которую боятсяСкачать

Как найти объем цилиндра если в него вписан правильный треугольник

Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.

Радиусы шара и основания цилиндра равны. Площадь поверхности цилиндра, с радиусом основания r и высотой 2r равна

Площадь поверхности шара радиуса r равна то есть в 1,5 раза меньше площади поверхности цилиндра. Следовательно, площадь поверхности шара равна 12.

Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому площадь основания равна 4, а объем параллелепипеда равен

Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.

Высота параллелепипеда равна высоте вписанного в него цилиндра. Основанием параллелепипеда является квадрат, сторона которого в два раза больше радиуса вписанной в него окружности. Поэтому сторона основания равна 8, а площадь основания равна 64. Тогда высота цилиндра равна

Почему получилось 64? Что-то не понятно:(

Длина диаметра цилиндра равна длине стороны квадрата в основании.

В куб вписан шар радиуса 1. Найдите объем куба.

Ребро куба равно диаметру вписанного в него шара, а объем куба равен кубу его ребра. Отсюда имеем:

В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.

По теореме Пифагора длина гипотенузы треугольника в основании Поскольку гипотенуза является диаметром основания описанного цилиндра, его объем

Видео:Миникурс по геометрии. Куб, призма, цилиндр и конусСкачать

Как найти объем цилиндра если в него вписан правильный треугольник

Примечание. Это часть урока с задачами по геометрии (раздел стереометрия). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. В задачах вместо символа «квадратный корень» применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение.

Видео:Задачи на нахождения объема призмы и цилиндраСкачать

Задача. Призма, вписанная в цилиндр

В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет которого равен 2а, а прилежащий угол равен 60 градусам. Диагональ большей боковой грани призмы составляет с плоскостью ее основания угол в 45 градусов. Найдите объем цилиндра.

Решение .
Объем цилиндра найдем по формуле:

где:
R — радиус основания прямого цилиндра,
h — высота.

Найдем основание цилиндра. 1-й способ .
Основание цилиндра одновременно является окружностью, описанной вокруг прямоугольного треугольника, являющегося основанием призмы. Диаметр окружности, описанной вокруг прямоугольного треугольника, лежит на его гипотенузе. То есть длина гипотенузы равна 2R.

Радиус окружности, описанной вокруг треугольника найдем по формуле:

R = x / 2 sin α
где:
x — сторона треугольника
α — угол, противолежащий стороне а.

Противолежащий угол найдем следующим образом. Поскольку треугольник прямоугольный, то противолежащий катету угол будет равен 180-90-60 = 30 градусов. Таким образом, радиус описанной окружности (он же радиус цилиндра) равен:

Найдем основание цилиндра. 2-й способ
У прямоугольного треугольника гипотенуза одновременно является диаметром описанной окружности. Половина гипотенузы будет равна ее радиусу.
Таким образом найдем гипотенузу для прямоугольного треугольника, зная угол и его катет через тригонометрическую функцию:
2R = 2a / cos 60 = 2a / 0.5 = 4a
R = 2a

Найдем высоту цилиндра .
Диаметр описанной окружности образует с диагональю призмы прямоугольный треугольник, один катет которого является диаметром описанной окружности, второй — высотой цилиндра и призмы, а гипотенуза является диагональю большей стороны призмы и одновременно цилиндра.

Поскольку угол диагонали с основанием составляет 45 градусов, то второй угол равен 180 — 45 — 90 = 45 градусов.
Исходя из того, что прямоугольный треугольник равнобедренный, то высота цилиндра и призмы равна диаметру окружности. Таким образом:

V = пR 2 h
V = п*4a 2 *4a
V = п16a 3 .

Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Задача. В цилиндр вписана правильная шестиугольная призма

В цилиндр вписана правильная шестиугольная призма. Найти угол между диагональю ее боковой грани и осью цилиндра, если радиус основания равен высоте цилиндра.

Если радиус основания равен высоте цилиндра, диагональ боковой грани правильной шестиугольной призмы представляет собой прямоугольный треугольник, у которого один из катетов равен высоте цилиндра (r), а второй катет равен стороне шестиугольника, вписанного в окружность.Согласно свойствам шестиугольника, вписанного в окружность, его сторона равна радиусу такой окружности.

То есть, каждая боковая грань данной вписанной призмы – квадрат. Диагональ грани образует с осью цилиндра, как и с боковым ребром, одинаковый угол 45°, так как ось цилиндра и боковые ребра вписанной призмы параллельны.

Видео:11 класс, 32 урок, Объем цилиндраСкачать

В окружность основания цилиндра вписан правильный треугольник.Найти объем пирамиды той же высоты что и цилиндр,в основании которого лежит этот треугольник,если объем цилиндра равен π√3

Острый угол равен 60 градусов, значит, тупой равен 180-60=120 градусов. меньшая диагональ ромба является биссектрисой его тупого угла. Угол между стороной и диагональю равен 120/2=60 градусов. В треугольнике, образованном двумя сторонами ромба и меньшей диагональю, два угла равны 60 градусов, значит, этот треугольник равносторонний => меньшая диагональ равна стороне ромба.

В ромбе все стороны равны.

Периметр равен a+a+a+a=24,8 м (а-сторона)

вроде 2, это нужно делать по теареме

Осевое сечение конуса — это равнобедренный треугольник. Следовательно, угол при вершине делится высотой конуса пополам. Тогда в прямоугольном треугольнике, образованном высотой конуса, его радиусом (катеты) и образующей (гипотенуза) Образующая L=2R, так как радиус лежит против угла 30°. Учитывая, что R = (2-L) см (дано), можем написать: L =2*(2-L) см. => L=4-2L, => L=4/3 см.

Площадь полной поверхности конуса равна сумме площадей основания и боковой поверхности, то есть S = So +Sб, или S=π(R²+R*L). подставляя найденные значения, получим

S = π(4/9+2*4/(3*3)) = 12/9 = 4/3см² = 1и1/3 см².

Видео:Призма и цилиндр. Практическая часть. 11 класс.Скачать