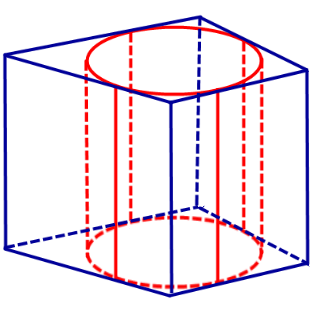
Как найти объем цилиндра описанного вокруг призмы (2 видео)

Содержание

Цилиндры, вписанные в призмы. Свойства призмы, описанной около цилиндра
Отношение объемов цилиндра и описанной около него правильной n — угольной призмы
Геометрия. 11 класс
📽️ Видео

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Цилиндры, вписанные в призмы. Свойства призмы, описанной около цилиндра

Определение 2. Если цилиндр вписан в призму, то призму называют описанной около цилиндра.

Прежде, чем перейти к вопросу о том, в какую же призму можно вписать цилиндр, докажем следующее свойство призм.

Утверждение 1. Если в основания призмы можно вписать окружности, то отрезок, соединяющий центры вписанных окружностей, будет параллелелен и равен боковому ребру призмы.

Рассуждая аналогичным образом, заключаем, что точка O’ равноудалена от всех прямых, на которых лежат ребра верхнего основания A’₁A’₂, A’₂A’₃, . , A_{n – 1}A_n , а поскольку O’ лежит в плоскости верхнего основания, то точка O’ является центром вписанной в многоугольник A’₁A’₂ . A’_n окружности.

В силу того, что прямые OO’ и A₁A’₁ параллельны по построению, а прямые OA₁ и O’A’ параллельны как линии пересечения двух параллельных плоскостей третьей плоскостью, замечаем, что четырехугольник OO’A₁A’₁ является параллелограммом, откуда вытекает равенство: OO’ = A₁A’₁ .

Теорема. В призму можно вписать цилиндр тогда и только тогда, когда выполнены следующие два условия:

Призма является прямой призмой;
В основания призмы можно вписать окружности.

Доказательство. Докажем сначала, что если в n – угольную призму вписан цилиндр, то оба условия теоремы выполнены.

Действительно, выполнение условия 2 следует непосредственно из определения цилиндра, вписанного в призму. Докажем, что выполняется и условие 1, т.е. докажем, что описанная около цилиндра призма является прямой призмой.

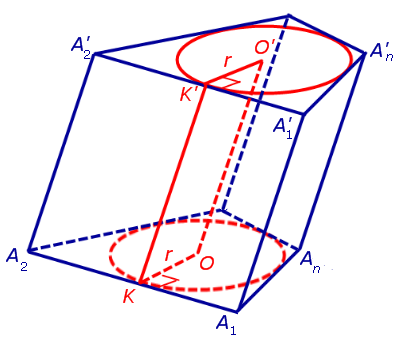
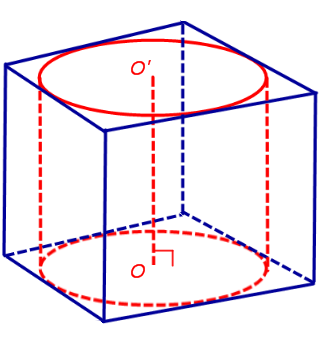
С этой целью рассмотрим ось цилиндра OO’ , соединяющую центры окружностей, вписанных в нижнее и верхнее основания призмы (рис. 3).

Согласно утверждению 1 отрезок OO’ параллелен боковым ребрам призмы. Поскольку ось цилиндра OO’ перпендикулярна к плоскостям его оснований, то и боковые ребра призмы также перпендикулярны к плоскостям оснований, то есть призма является прямой призмой.

Читайте также: Прокачка заднего тормозного цилиндра ваз 2114

Таким образом, мы доказали, что, если призма описана около цилиндра, то оба условия теоремы выполнены.

Теперь рассмотрим прямую n – угольную призму высоты h, в основания которой можно вписать окружности, и докажем, что в такую призму можно вписать цилиндр.

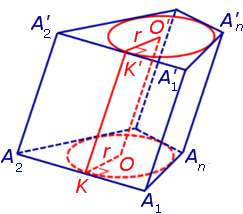
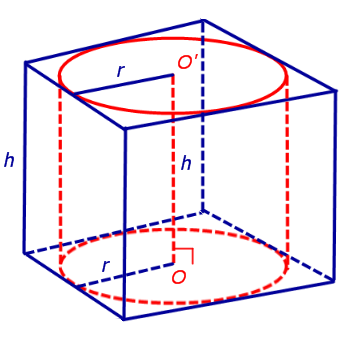
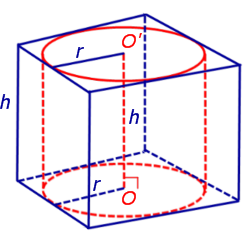
Обозначим буквой O центр окружности радиуса r, вписанной в нижнее основание призмы, а символом O’ обозначим центр окружности, вписанной в верхнее основание призмы (рис. 4).

Поскольку многоугольники, лежащие в основаниях призмы равны, то и радиусы вписанных в них окружностей будут равны. Согласно утверждению 1 отрезок OO’ параллелен и равен боковому ребру призмы. Так как рассматриваемая призма прямая, то ее боковые ребра перпендикулярны плоскости основания и равны высоте призмы h. Значит, и отрезок OO’ перпендикулярен плоскости основания призмы и равен h.

Цилиндр с осью OO’ , радиусом r и высотой h и будет вписан в исходную призму.

Доказательство теоремы завершено.

Следствие 1 . Высота призмы, описанной около цилиндра, равна высоте цилиндра.

Следствие 2. В любую прямую треугольную призму можно вписать цилиндр.

Справедливость этого утверждения вытекает из того факта, что в любой треугольник можно вписать окружность.

Следствие 3. В любую правильную n – угольную призму можно вписать цилиндр.

Для доказательства этого следствия достаточно заметить, правильная призма является прямой призмой. Основаниями правильной призмы являются правильные многоугольники, а в любой правильный n – угольник можно вписать окружность.

Видео:Цилиндр - расчёт площади, объёма.Скачать

Отношение объемов цилиндра и описанной около него правильной n — угольной призмы

Задача. Найти отношение объемов цилиндра и описанной около него правильной n — угольной призмы.

Решение. Поскольку и объем цилиндра, и объем призмы объем призмы вычисляются по формуле

а высота цилиндра равна высоте описанной около него призмы, то для объемов цилиндра и описанной около него правильной n — угольной призмы справедливо равенство

Следствие 4. Отношение объема цилиндра к объему описанной около него правильной треугольной призмы правильной треугольной призмы равно

Следствие 5. Отношение объема цилиндра к объему описанной около него правильной четырехугольной призмы правильной четырехугольной призмы равно

Читайте также: Палец цилиндра гур мтз

Следствие 6. Отношение объема цилиндра к объему описанной около него правильной шестиугольной призмы равно

Видео:ЕГЭ математика СТЕРЕОМЕТРИЯ 8#5.18🔴Скачать

Геометрия. 11 класс

Конспект урока

Урок №12. Объемы прямой призмы и цилиндра

Перечень вопросов, рассматриваемых в теме

1) Доказательство теорем об объемах прямой призмы и цилиндра

2) Определение призмы, вписанной в цилиндр и призмы описанной около цилиндра

3) Решение задач на нахождение объемов прямой призмы и цилиндра

V=Sh объем прямой призмы и цилиндра

Бутузов В. Ф., Кадомцев С. Б., Атанасян Л. С. и др. Геометрия. 10–11 классы : учеб.для общеобразоват. организаций : базовый и углубл. Уровни – М.: Просвещение, 2014. – 255, сс. 121-126.

Шарыгин И.Ф. Геометрия. 10–11 кл.: учеб.для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 178-196.

Потоскуев Е.В., Звавич Л. И., Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 5-30.

Теоретический материал для самостоятельного изучения

Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.

Прямая призма — это призма, у которой боковые ребра перпендикулярны плоскости основания, откуда следует, что все боковые грани являются прямоугольниками

Объем всякого цилиндра равен произведению площади основания на высоту

Объем призмы — это произведение площади ее основания на высоту

Призма вписана в цилиндр, если ее основания вписаны в основания цилиндра.

Призма описана около цилиндра, если ее основания описаны около оснований цилиндра.

Высота любой призмы (вписанной в цилиндр или описанной около цилиндра), равна высоте самого цилиндра

Примеры и разбор решения заданий тренировочного модуля

№1. Найти объем прямой треугольной призмы высотой 6, в основании которой — прямоугольный треугольник с катетами 3 и 7.

Решение: Объем призмы вычисляется по формуле , т.к. в основании призмы – прямоугольный треугольник, то объем призмы будет вычисляться по формуле , где а и в – катеты треугольника. Подставляя все данные задачи в формулу, получаем ответ: .

Читайте также: Как определить утечку антифриза в цилиндр двигателя

№2. Найти объём правильной -угольной призмы, у которой каждое ребро равно а, если: а) n=3, б) n=4, в) n=6.

Решение: поскольку призма правильная, значит, это прямая призма и в основании лежит правильный многоугольник.

Формулу для вычисления объёма прямой призмы мы только что вывели . Поскольку, по условию все ребра призмы равны a, значит, высота призмы равна h=a. Осталось найти площадь основания.

Основанием правильной треугольной призмы является правильный, то есть равносторонний треугольник n=3. Площадь правильного треугольника со стороной f вычислить несложно, она равна .

Применяя формулу для вычисления объёма прямой призмы, получим, что объём правильной треугольной призмы равен .

Основанием правильной четырёхугольной призмы является квадрат n=4. Площадь квадрата со стороной a равна . Тогда объём правильной четырёхугольной призмы равен .

Основанием правильной шестиугольной призмы является правильный шестиугольник n=6. Своими большими диагоналями шестиугольник делится на 6 равносторонних треугольников. Площадь каждого из треугольников равна , значит, площадь правильного шестиугольника равна . Тогда объём правильной шестиугольной призмы равен .

Ответ 3/2 ед 3

№3 Найди объём прямой призмы если =120°, АВ=5 см, ВС=3см и наибольшая из площадей боковых граней равна 35см 2 .

Решение: боковая грань прямой призмы является прямоугольником.

Площадь каждой боковой грани равна произведению высоты призмы на сторону основания.

То есть большая боковая грань содержит большую сторону основания.

По условию =120°, – тупой, а поскольку напротив большей стороны лежит больший угол, то большей стороной основания будет сторона АС. Вычислим длину стороны АС по теореме косинусов.