Найти чему равен объем цилиндра (V) можно зная (либо-либо):
- радиус r и высоту h цилиндра
- диаметр d и высоту h цилиндра
- площадь основания So и высоту h цилиндра
- площадь боковой поверхности Sb и высоту h цилиндра
Подставьте значения в соответствующие поля и получите результат.
- Зная радиус r и высоту h
- Формула
- Пример
- Зная диаметр d и высоту h
- Формула
- Пример
- Зная площадь основания So и высоту h
- Формула
- Пример
- Зная площадь боковой поверхности Sb и высоту h
- Формула
- Пример
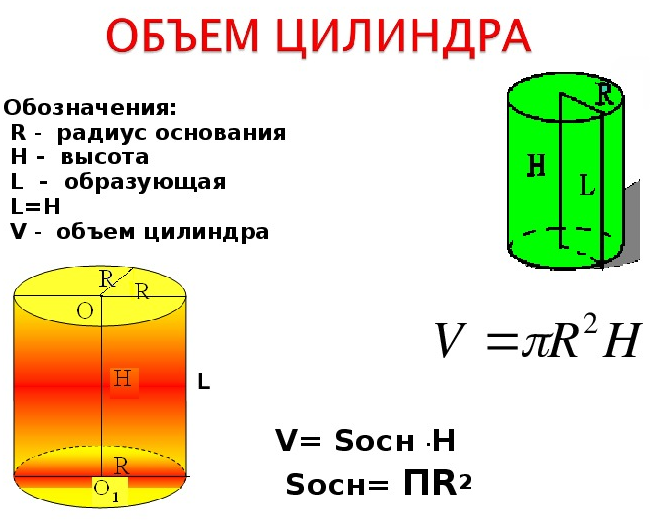
- Объем цилиндра
- Объем правильного цилиндра через радиус и высоту цилиндра
- Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра
- Формулы и калькулятор для вычисления объема цилиндра через диаметр основания
- Объем цилиндрической полости
- Поверхности цилиндра
- Сечения цилиндра
- Что такое объем
- Объем жидкости в цилиндрической таре
- Объем жидкости в цилиндрической таре
- Объем цилиндра
- Смотрите также
- Нахождение объема цилиндра: формула и задачи
- Формула вычисления объема цилиндра
- Через площадь основания и высоту
- Через радиус основания и высоту
- Через диаметр основания и высоту
- Примеры задач
- Как найти объем воздуха в цилиндре
- 💥 Видео
Зная радиус r и высоту h
Чему равен объем цилиндра V если известны его радиус r и высота h?
Формула
Пример
Если цилиндр имеет высоту h = 8 см, а его радиус r = 2 см, то:
V = 3.14156 ⋅ 2 2 ⋅ 8 = 3.14156 ⋅ 32 = 100.53 см 3
Зная диаметр d и высоту h
Чему равен объем цилиндра V если известны его диаметр d и высота h?
Формула
Пример
Если цилиндр имеет высоту h = 5 см, а его диаметр d = 1 см, то:
V = 3.14156 ⋅ ( 1 /2) 2 ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см 3
Зная площадь основания So и высоту h
Чему равен объем цилиндра V если известны его площадь основания So и высота h?
Формула
Пример
Если цилиндр имеет высоту h = 10 см, а площадь его основания So = 5 см 2 , то:
Зная площадь боковой поверхности Sb и высоту h
Чему равен объем цилиндра V если известны его площадь боковой поверхности Sb и высота h?
Формула
Пример
Если цилиндр имеет высоту h = 5 см, а площадь его боковой поверхности Sb = 30 см 2 , то:
V = 30 2 / 4 ⋅ 3.14⋅ 5 = 900 /62.8 = 14.33 см 3
Видео:"ГТ" ПРОСТЕЙШИЙ СПОСОБ ПРОВЕРКИ ПОДСОСА ВОЗДУХА!!!Скачать

Объем цилиндра
Объем цилиндра, формулы и калькулятор для вычисления объема цилиндра и площади его поверхностей, а также необходимая теория о характеристиках цилиндра.
Видео:Объём цилиндраСкачать

Объем правильного цилиндра через радиус и высоту цилиндра
Видео:Задача про ЦИЛИНДР / Как найти объем детали? / Профиль ЕГЭСкачать

Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндра
Видео:ПОДСОС ВОЗДУХА - НАЙТИ БЕЗ ДЫМОГЕНЕРАТОРАСкачать

Формулы и калькулятор для вычисления объема цилиндра через диаметр основания
Видео:11 класс. Геометрия. Объем цилиндраСкачать

Объем цилиндрической полости
Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.
На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.
Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.
Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.
Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.
Рассмотрим правильный цилиндр.
Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник
Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра.
Радиус основания цилиндра, является радиусом цилиндра.
Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.
Читайте также: Главный рабочий цилиндр сцепления акцент
Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.
Видео:Объем цилиндраСкачать

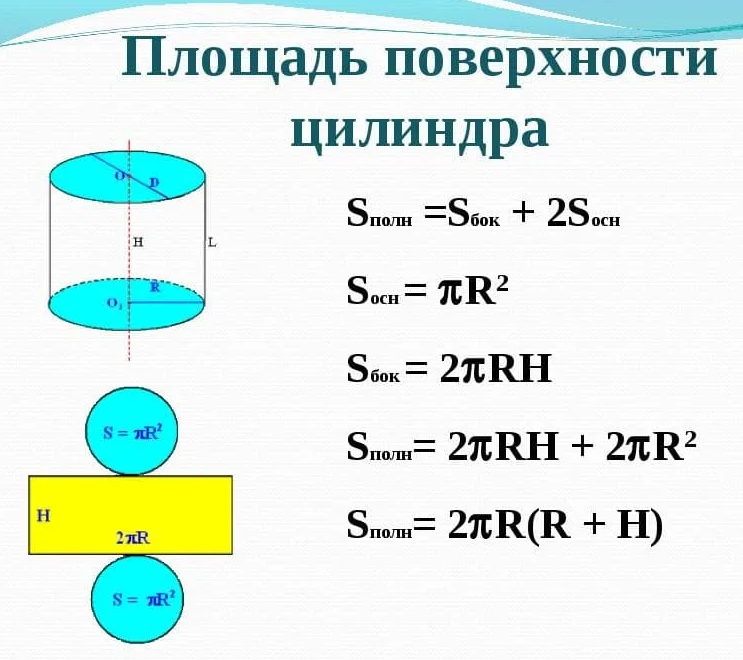
Поверхности цилиндра
Наружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая.
Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой.
Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке).
Видео:Пневмотестер - как это работает? Ищем утечки в цилиндре!Скачать

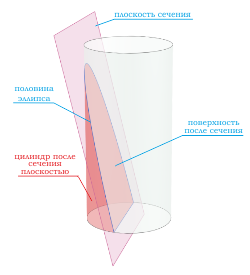
Сечения цилиндра
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура .
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник , но две боковые стороны которого будут являться кривыми линиями.
Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг .
Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс .
Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса .
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Что такое объем
Объем тела (геометрической фигуры) – это количественная характеристика, характеризующая количество пространства, занимаемого телом. Объем выражается в кубических единицах измерения, например: мм 3 , см 3 , мл 3 .
Формула вычисления объема цилиндра часто применяются при расчете массы различных цилиндров, например, прутков, заготовок и т.п. Для вычисления массы, необходимо вычисленный объем цилиндра умножить на плотность материала из которого цилиндр.
Так же, вычислить объём цилиндра иногда требуется для определения полости в виде цилиндра (цилиндрическая полость). В данном случае объём полости будет равен объёму цилиндра, который полностью занимает эту полость.
Объем и площадь других видов цилиндров рассмотрен в статьях:
Видео:Относительная влажность воздуха в цилиндре под поршнем равна 75. Объём воздуха изотремически - №Скачать

Объем жидкости в цилиндрической таре
Расчет объема жидкости в цилиндрической таре, лежащей на боку (создано по запросу пользователя).
Ага, сегодня я путем несложных умозаключений буду выяснять объем жидкости, находящейся в цилиндрической таре, лежащей на боку.
И это не праздности ради, а дела для.
Цитирую запрос пользователя объем сегмента цилиндра (2):
Доброго времени суток. Видел калькулятор объема сегмента цилиндра, но нужно немножко другое. По работе приходится измерять количество жидкости в таре. Так вот допустим тара цилиндрической формы R=1,13м и H=6,3м лежит на поверхности. Жидкости в таре 0,9м от поверхности. Вопрос: какой объем жидкости в таре?
Там дальше в запросе идут ссылки на решение, но это же не спортивно, поэтому я пошел своим путем ? Сразу замечу, что вторая, более сложная задача — объем жидкости в таре, лежащей под наклоном, еще ждет своего решения.
Вот калькулятор, который все считает, а ход рассуждений, как обычно, под ним.
Объем жидкости в цилиндрической таре
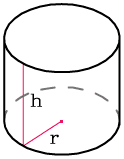
Итак, сформулируем задачу наглядно, и посмотрим на цилиндр в разрезе (см. рисунок). Если уровень жидкости m больше половины, то находим объем воздуха в оставшейся части, а потом вычитаем из общего объема — т. е. всегда сводим к случаю, изображенному на рисунке.
Формула объема всего цилиндра известна — площадь основания, помноженная на высоту.
А нам, значит, надо найти площадь фигуры, залитой синей жидкостью, и тоже помножить на высоту. Пытливый взгляд отметит, что фигура, залитая синей жидкостью, получается из сектора после вычета верхнего треугольника.
Площадь сектора находится как
, где альфа — это угол дуги в радианах.
Угол дуги нам неизвестен. Разберемся сначала с ним. Линия, опущенная вертикально вниз делит верхний треугольник на два прямоугольных треугольника. Гипотенуза у них равна R, а катет, прилежащий к верхнему углу, равен R-m. Таким образом,
Читайте также: Как восстановить задний тормозной цилиндр
и ответ нам Javascript даст как раз в радианах, то что нам нужно.
Теперь разберемся с верхним треугольником. Он равнобедренный, бедра равны R, а основание нам неизвестно. Найдем его.
А оно как раз равно удвоенному противолежащему катету, который, согласно всем известной теореме Пифагора равен
Зная все стороны треугольника, нетрудно найти его площадь по формуле Герона — Расчет площади треугольника по формуле Герона.
Вот, собственно, и все. Мы знаем площадь сектора и площадь треугольника. Вычитаем площадь треугольника из площади сектора, домножаем на высоту цилиндра (или длину цилиндра, с учетом того, что он лежит) и получаем результат.
Видео:Как просто поднять компрессию в цилиндрах, без разборки мотора!Скачать

Объем цилиндра
Цилиндр – это геометрическое тело, которое имеет цилиндрическую поверхность, называемое еще как боковая поверхность цилиндра и имеет две поверхности, которые носят название оснований цилиндра. Круговым цилиндр называют, если у него в основании лежит круг.
Если вам необходимо вычислить объем цилиндра, то прежде, чем начать его вычисление отставьте прочь калькуляторы и свои методы решения. Ведь теперь у вас есть более легкий способ решить такую задачу, а именно наш онлайн калькулятор, который сэкономит ваше время и лишит возможности ошибиться. Все что от вас требуется это ввести несколько значений. Причем мы предлагаем два способа решения с любым из неизвестных.
Первый способ наш онлайн калькулятор вычисляет по формуле: , а второй по формуле
Где S – это площадь основания, h – это высота цилиндра, число пи равное 3.14159, а r— это радиус цилиндра.
Смотрите также
Спасибо, очень полезным оказался
Спасибо, очень удобный калькулятор. Вспомнила формулу вычисления объёма. Невозможно держать в голове всю школьную программу. Пользуешься только необходимыми вычислениями, которые нужны для моей профессии.
А в каких единицах измерения, в бананах или коровах? Услугами данного калькулятора пользуются не профессора! Бесполезно потраченное время!
Оксана, результат у тебя, и таких как ты, получится в кубических курах. Потому, что у вас мозги куриные!
В школу ходить надо было.
Если измерение проводится в см, то и получаете см возведённые в куб.
Учитель не до конца вам объяснил или вы не усвоили, что в геометрии как правило объем измеряется в кубах, соответственно:
— Если вводите в бананах, то результат будет в бананах кубических,
— Если в сантиметрах, то результат будет в сантиметрах кубических (см³).
и т.д.
Слушайте учителей, образовывайтесь, заставляйте свой мозг работать.
Не нужно быть профессором чтобы воспользоваться этим калькулятором
Разницы нету метры, сантимеры, миллиметры он вам выдаёт куб того что вы ввели.
Видео:Урок 28 (осн). Вычисление массы и объема тела по плотностиСкачать

Нахождение объема цилиндра: формула и задачи
В данной публикации мы рассмотрим, как можно найти объем цилиндра и разберем примеры решения задач.
Видео:Физика При сжатии воздуха в цилиндре дизельного двигателя объем воздуха уменьшается в 15 разСкачать

Формула вычисления объема цилиндра
Через площадь основания и высоту
Объем (V) цилиндра равняется произведению его высоты и площади основания.
Через радиус основания и высоту
Как мы знаем, в качестве оснований цилиндра (равны между собой) выступает круг, площадь которого вычисляется так: S = π ⋅ R 2 . Следовательно, формулу для вычисления объема цилиндра можно представить в виде:
V = π ⋅ R 2 ⋅ H
Примечание: в расчетах значение числа π округляется до 3,14.
Через диаметр основания и высоту
Как нам известно, диаметр круга равняется двум его радиусам: d = 2R. А значит, вычислить объем цилиндра можно следующим образом:
Видео:5 способов найти подсос воздуха в двигатель.Скачать

Примеры задач
Задание 1
Найдите объем цилиндра, если дана площадь его основания – 78,5 см 2 , а также, высота – 10 см.
Решение:
Применим первую формулу, подставив в нее известные значения:
V = 78,5 см 2 ⋅ 10 см = 785 см 3 .
Задание 2
Высота цилиндра равна 6 см, а его диаметр – 8 см. Найдите объем фигуры.
Решение:
Воспользовавшись третьей формулой, в которой участвует диаметр, получаем:
V = 3,14 ⋅ (8/2 см) 2 ⋅ 6 см = 301,44 см 3 .
Видео:✅ Как быстро проверить подсос воздуха во всасывающем коллекторе и не только.Скачать

Как найти объем воздуха в цилиндре
Тонкостенный цилиндр с воздухом закрыт снизу поршнем массой m = 3 кг, который может без трения перемещаться в цилиндре. Цилиндр плавает в вертикальном положении в воде при температуре T = 300 К (см. рис.). Когда цилиндр опустили при постоянной температуре на глубину h = 10 м (от поверхности воды до его верхней крышки), он потерял плавучесть. Найдите массу воздуха в цилиндре. Атмосферное давление равно p0 = 10 5 Па, масса цилиндра и воздуха в цилиндре гораздо меньше массы поршня.
Читайте также: Мазда mpv порядок работы цилиндров
Поскольку цилиндр лёгкий, а трения между ним и поршнем нет, то при плавании воздух в цилиндре находится под атмосферным давлением Обозначим объём воздуха в цилиндре при плавании через Тогда, согласно уравнению Клапейрона — Менделеева, где — искомая масса воздуха.
Неизвестный объём воздуха при атмосферном давлении можно найти из следующих соображений. Сила Архимеда, действующая на цилиндр с поршнем при его плавании и в момент потери плавучести, одна и та же и равна весу поршня: где — плотность воды, а — объём вытесненной воды, равный объёму воздуха в цилиндре в момент потери плавучести. Согласно закону Бойля — Мариотта, при изотермическом процессе Поскольку по условию масса цилиндра пренебрежимо мала и трение между поршнем и цилиндром отсутствует, в равновесии давления на верхнюю грань цилиндра с обеих сторон одинаковы:
I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае — формула для внутренней энергии идеального газа, условие установления равновесия в сосуде);
II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, обозначений величин, используемых в условии задачи и стандартных обозначений величин, используемых при написании физических законов);
III) проведены необходимые математические преобразования, приводящие к правильному ответу;
Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют.
Лишние записи, не входящие в решение (возможно, неверные), не отделены от решения (не зачёркнуты, не заключены в скобки, рамку и т. п.).
В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) преобразования/вычисления не доведены до конца.
Представлены только положения и формулы, выражающие физические законы, применение которых необходимо для решения задачи, без каких-либо преобразований с их использованием, направленных на решение задачи, и ответа.
В решении отсутствует одна из исходных формул, необходимая для решения задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
«Поскольку цилиндр лёгкий, а трения между ним и поршнем нет, то при плавании воздух в цилиндре находится под атмосферным давлением Обозначим объём воздуха в цилиндре при плавании через Тогда, согласно уравнению Клапейрона–Менделеева, где — искомое количество воздуха.»
Это не так, поскольку мы видим, что на какую-то часть поршень погружен в воду. Поэтому давление в цилиндре будет равно Po+плотность воды *g*hводы до дна поршня.
Соответственно, когда поршень в воде полностью давление на дно поршня будет уравновешивать давление внутри поршня. И оно будет Po+плотность воды*g*hводы до дна поршня.
Поршень имеет ненулевую массу, поэтому давление газа сверху не равно давлению воды снизу. А вот цилиндр «лёгкий», поэтому давление воздуха снаружи равно давлению внутри.
💥 Видео
Какие должны быть показатели параметров при диагностике исправного автомобиляСкачать

Относительная влажность воздуха в цилиндре под поршнем равна 73. Воздух в конечное его давление - №Скачать

Как влияет на работу двигателя подсос воздуха.Скачать

!!!Как найти подсос воздуха в двигателе автомобиля ваз, быстро без приборовСкачать

1 часть: 1-й признак отсутствия компрессии из-за износа поршневой группы, Sprinter 316CDI 2.7Скачать

Пропуски зажигания, воспламенения в цилиндрах, подсос воздуха и устранение неполадкиСкачать