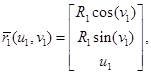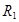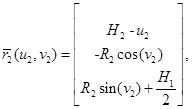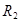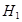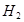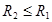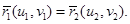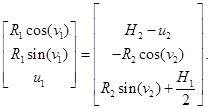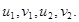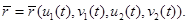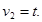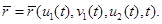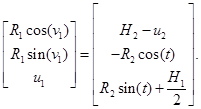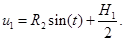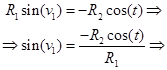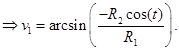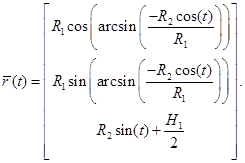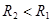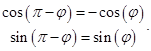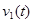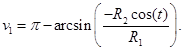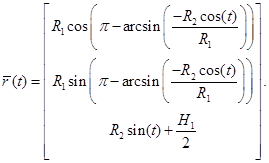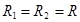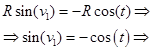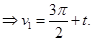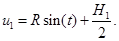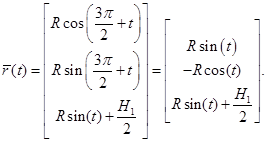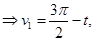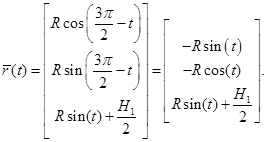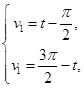Как найти пересечение двух цилиндров

На рис. 197 приведен случай пересечения двух цилиндров под прямым углом. Горизонтальные проекции линий пересечения совпадают с контуром вертикально расположенного цилиндра. Пересечение фронтальных проекций крайних образующих линий цилиндров определяет точки 1₂, 2₂, 3₂ и 4₂ С помощью горизонтальных проекций 5₁ и 6₁ находят фронтальные проекции 5₂ и 6₂ передних точек линий пересечения. Для нахождения промежуточных точек проводят горизонтальную плоскость ?. Эта плоскость пересечет вертикальный цилиндр по окружности, горизонтальная проекция которой совпадает с контуром этого цилиндра. Горизонтально расположенный цилиндр пересечется с плоскостью ? по образующим, которые удобнее найти с помощью третьей проекции (точки 73, 83). При отсутствии третьей проекции пользуются вспомогательной полуокружностью плоскости П₂. Она позволяет определить расстояние у от образующих до оси цилиндра. Получив горизонтальную проекцию 7₁ находят ее фронтальную проекцию 7₂ на фронтальной проекции ?₂ плоскости-посредника ?. Задачу решают путем проведения ряда таких плоскостей.

TBegin:http://polynsky.com.kg/uploads/posts/2010-09/1284966965_two-cylinders.jpg|—>TEnd—>

Линию пересечения в изометрической проекции строят с помощью одного из оснований цилиндров, в данном случае с помощью левого основания горизонтального цилиндра. От соответствующих точек этого основания по образующим откладывают величины, взятые с фронтальной или горизонтальной проекций цилиндра. Таким путем на чертеже построены точки 7′, 5′ и обведена четвертая часть передней (левой) линии пересечения; другие точки линии пересечения находятся аналогично; задняя (правая) линия пересечения в этом примере будет невидимой.

Видео:Как построить ЛИНИЮ ПЕРЕСЕЧЕНИЯ двух ЦИЛИНДРОВСкачать

уравнение пересечения двух цилиндров

Для просмотра формул ваш браузер должен поддерживать MathML.

Стало интересно построить линию пересечения двух цилиндров не методами начертательной геометрии.

Насколько я понимаю, кривая должна описываться системой, например, таких уравнений

Вопрос такой.
Правильно ли я записал систему. описывающую кривую, как такую кривую можно построить (например в какой-то программе), как добиться нагядности, есть ли альтернативные варианты задания такой кривой? по сути система аналитически описывает условие для задания места в пространстве, к которому принадлежали точки обоих бесконечных цилиндров. но вид кривой для меня не очевиден, когда я смотрю на эту систему

Пересекаются по двум эллипсам. Если хотите записать их аналитически, вычтите одно уравнение из другого. Вы увидите, что линии пересечения лежат в плоскостях $y = z, y = -z$ .

Для построения Ваши эллипсы удобно задать параметрически:

$x=\cos t$ , $y=\sin t$ , $z=\sin t$ — первый эллипс
$x=\cos t$ , $y=\sin t$ , $z=-\sin t$ — второй эллипс

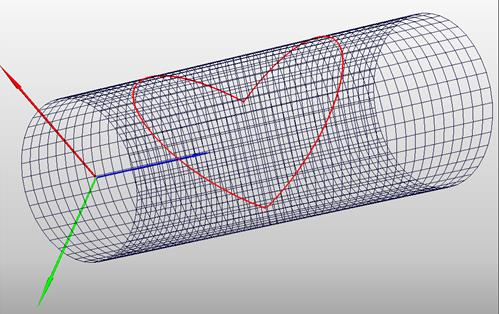
Построить, я думаю, можно в любом матпакете. Построение в Maple (вместе с цилиндрами и отдельно):

Читайте также: Что такое бачок главного тормозного цилиндра

A := plots[implicitplot3d]([x^2+y^2 = 1, x^2+z^2 = 1], x = -2 .. 2, y = -2 .. 2, z = -2 .. 2, style = surface, color = grey, numpoints = 25000, axes = normal):
B := plots[spacecurve]([cos(t), sin(t), sin(t)], t = 0 .. 2*Pi, color = red, thickness = 4):
C := plots[spacecurve]([cos(t), sin(t), -sin(t)], t = 0 .. 2*Pi, color = blue, thickness = 4):
plots[display](A, B, C, view = [-2.9 .. 2.9, -2.9 .. 2.9, -2.9 .. 2.9], lightmodel = light4, orientation = [30, 75]);
plots[display](B, C, view = [-2.9 .. 2.9, -2.9 .. 2.9, -2.9 .. 2.9], lightmodel = light4, orientation = [30, 75], axes = normal;)

Цитата
kitonum
Для построения Ваши эллипсы удобно задать параметрически:

$x=\cos t$ , $y=\sin t$ , $z=\sin t$ — первый эллипс
$x=\cos t$ , $y=\sin t$ , $z=-\sin t$ — второй эллипс

Построить, я думаю, можно в любом матпакете. Построение в Maple (вместе с цилиндрами и отдельно):

A := plots[implicitplot3d]([x^2+y^2 = 1, x^2+z^2 = 1], x = -2 .. 2, y = -2 .. 2, z = -2 .. 2, style = surface, color = grey, numpoints = 25000, axes = normal):
B := plots[spacecurve]([cos(t), sin(t), sin(t)], t = 0 .. 2*Pi, color = red, thickness = 4):
C := plots[spacecurve]([cos(t), sin(t), -sin(t)], t = 0 .. 2*Pi, color = blue, thickness = 4):
plots[display](A, B, C, view = [-2.9 .. 2.9, -2.9 .. 2.9, -2.9 .. 2.9], lightmodel = light4, orientation = [30, 75]);
plots[display](B, C, view = [-2.9 .. 2.9, -2.9 .. 2.9, -2.9 .. 2.9], lightmodel = light4, orientation = [30, 75], axes = normal;)

Видео:Задание 50. Построение ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ЦИЛИНДРОВСкачать

Пересечение двух цилиндров

Пересечение двух цилиндров является одной из основных задач начертательной геометрии, выполнение которой требует знания основ создания проекций.

Рассмотрим пример пересечения двух цилиндров под прямым углом из курса начертательной геометрии. Они параллельны профильной плоскости проекции (подразумевается, что оси вращения не пересекаются, а смещены друг от друга на некоторую величину а).

Ось малого цилиндра является перпендикулярной к горизонтальной плоскости проекции. Фронтальная проекция пересечения совпадает с очертанием большего цилиндра на отрезке между точками 1 и 7.

Таким образом, задача сводится к нахождению точек линии пересечения на проекции (профильной).

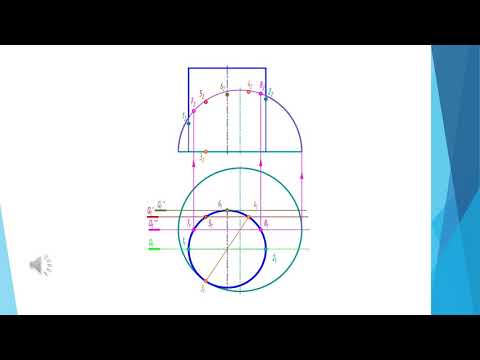
1. Для этого удобно применить вспомогательные секущие плоскости уровня. Для их равномерного расположения, проекцию основания вертикального цилиндра делят на 12 частей.
2. Затем через точки деления проводятся образующие, после чего выявляются точки их пересечений с поверхностью горизонтального цилиндра (фронтальная проекция).
3. Профильные линии точек находятся по линиям связи.
4. Для начала построения аксонометрии пересекающихся цилиндров необходимо изобразить их очерки (рисунок б).
5. Для нахождения опорных точек на горизонтальном цилиндре можно построить контур нормального сечения вокруг точки В.
6. Для нахождения точек, которые принадлежат линии перехода, необходимо рассечь цилиндры вспомогательными плоскостями уровня. Они пересекут оба цилиндра по образующим.
7. В пересечениях соответствующих образующих находятся промежуточные (рис. в-д) и характерные точки (1,4,7,10) линии перехода, которую ищем.
8. Найденные точки соединяются плавной кривой.
9. Готовый изометрический вид пересечения двух цилиндров изображен на рисунке е.

Видео:Пересечение двух цилиндров: объем и площадь поверхности через двойной интегралСкачать

Тело пересечения цилиндров

Видео:Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

Построение линии пересечения двух цилиндров в параметрическом виде

Рубрика: 14. Общие вопросы технических наук

Статья просмотрена: 3136 раз

Библиографическое описание:

Князев, Д. Н. Построение линии пересечения двух цилиндров в параметрическом виде / Д. Н. Князев, Е. С. Устинова. — Текст : непосредственный // Технические науки в России и за рубежом : материалы IV Междунар. науч. конф. (г. Москва, январь 2015 г.). — Москва : Буки-Веди, 2015. — С. 122-125. — URL: https://moluch.ru/conf/tech/archive/124/7023/ (дата обращения: 29.10.2021).

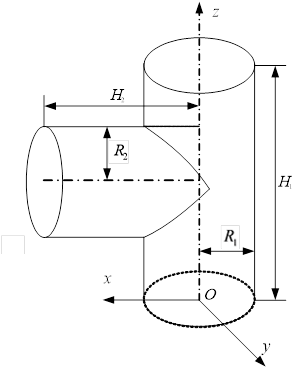
Для производства методом намотки из композиционных материалов элементов трансформируемых конструкций типа тройник, имеющего геометрическую форму двух пересекающихся цилиндров (рис. 1), необходимо иметь математическую модель такого объекта. Важным элементом такой модели является уравнение линии пересечения цилиндров.

Читайте также: Порядок работы цилиндров уаз 4213 инжектор

Рис. 1. Линия пересечения двух цилиндров

Параметрическое уравнение первого цилиндра (рис. 1) имеет вид:

(1)

где — радиус первого цилиндра.

Параметрическое уравнение второго цилиндра (рис. 1) имеет вид:

где — радиус второго цилиндра,

— высота первого цилиндра,

— высота второго цилиндра.

Для заданной конфигурации цилиндров зададим дополнительное условие, ограничивающее радиус второго цилиндра:.

Условие пересечения цилиндров выглядит следующим образом:

(2)

Последняя система уравнений содержит три уравнения и четыре неизвестных величины:

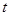
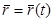
Введем для линии пересечения параметр , то есть — линия пересечения двух цилиндров.

(3)

Примем, что Тогда (3) запишется следующим образом:

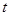
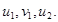
Теперь, так как параметр является задаваемой величиной, система (2) зависит от трех переменных: C учетом этого перепишем систему (2) следующим образом:

(4)

Из третьего уравнения системы (4) имеем:

(5)

Из второго уравнения системы (4) имеем:

(6)

Подставив (5) и (6) в систему (1), получим систему уравнений для линии пересечения цилиндров:

(7)

Линия пересечения при значении радиусов цилиндров представлена на рисунке 2.

Рис. 2. Линия пересечения цилиндров разного радиуса

Первое уравнение системы (7) дает положительные значения координаты X, что позволяем нам задать уравнения линии пересечения в положительном направлении оси X. Для получения уравнения линии пересечения в отрицательном направлении оси X необходимо получить отрицательные значения первого уравнения системы (7).

Воспользуемся тригонометрическими формулами приведения:

Параметр принимает следующий вид:

Уравнение для второй линий пересечения принимает вид:

Изображение второй линии пересечения представлено на рисунке 3.

Рис. 3. Вторая линия пересечения

Рассмотрим частный случай, в котором значения радиусов цилиндров равны . Из второго уравнения системы (4), на основании известных тригонометрических формул приведения, получим:

(8)

Из третьего уравнения системы (4) имеем:

(9)

Подставив (8) и (9) в систему (1), получим уравнение линии пересечения цилиндров (уравнение первого эллипса) равного радиуса:

(10)

Выражение для :

(11)

также является верным, так как с его помощью можно выразить уравнение второго эллипса, по которому пересекаются цилиндры, подставив (9) и (11) в систему (1). Уравнение второй линии пересечения имеет вид:

(12)

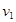
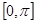
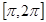
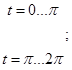
Системы уравнений (10) и (12) определяют эллипсы пересечения цилиндров. Для удобства рассмотрения выделим линии пересечения в положительном и отрицательном направлении оси Х через переопределение на интервалах и :

(13)

Используя для определения систему (13), можно получить линию пересечения цилиндров равного радиуса в положительном направлении оси Х, а используя систему (14) — в отрицательном.

Линия пересечения цилиндров равного радиуса в положительном направлении оси Х представлена на рисунке 4.

Рис. 4. Линия пересечения цилиндров равного радиуса

Видео:Пересечение поверхностей полусферы и цилиндра. Пошаговое видео. Инженерная графикаСкачать

Похожие статьи

Способ создания линии пересечения поверхностей вращения

Построение линии пересечения двух цилиндров. Уравнение для второй линий пересечения принимает вид: Изображение второй линии пересечения представлено на рисунке 3. Линия пересечения цилиндров равного радиуса в положительном.

Линия пересечения цилиндров равного радиуса.

Рис. 1. Линия пересечения двух цилиндров. Параметрическое уравнение первого цилиндра (рис. 1) имеет вид: (1). Линия пересечения цилиндров равного радиуса в положительном направлении оси Х представлена на рисунке 4.

Исследование свойств поверхностей вращения с использованием.

Поверхность, задаваемая уравнением , называется двуполостным гиперболоидом. Если поверхность пересечь плоскостями z=h, то линия пересечения определяется системой уравнений

Читайте также: Объем полого цилиндра пример

Касательная. Задачи на касательную | Статья в журнале.

Составим уравнение касательной к графику заданной функции в точке : Так как эта прямая проходит через точку (2;3), то имеет место равенство , откуда находим: . Может ли касательная к кривой в какой-либо ее точке составлять острый угол с положительным направлением оси ?

Об определении некоторых геометрических параметров.

После решения системы уравнений (9) получим уравнение прямой D1D3

С целью определения точек пересечения линии наибольшего наклона плоскости S к горизонту, проходящую через т. D1, с периметром площади АВС, определим точки пересечения.

Математическое моделирование взаимодействия ионов.

Расположим дипольные частицы в плоскости цилиндра диаметром равном , ось цилиндра параллельна оси .

Проведём окружность с центром в точке Q и радиусом 2 см, находим точку пересечения

Тогда динамику движения частиц можно описать уравнениями системы (1–3).

Сечение поверхностей 2-го порядка общего вида по эллипсу.

Способ создания линии пересечения поверхностей вращения. Создание горизонтальной проекции линии пересечения по фронтальной проекции не является сложным.

Расчёт фундаментных плит методом конечных элементов

Построение линии пересечения двух цилиндров. Важным элементом такой модели является уравнение линии пересечения цилиндров. Из второго уравнения системы (4), на основании известных тригонометрических формул приведения.

Евклидова плоскость в четырехмерном пространстве

Построение линии пересечения двух цилиндров в параметрическом виде. Анализ и разработка измерительной установки для определения момента инерции тел вращения сложной формы.

Видео:Пересечение двух цилиндров. Инженерная графикаСкачать

Похожие статьи

Способ создания линии пересечения поверхностей вращения

Построение линии пересечения двух цилиндров. Уравнение для второй линий пересечения принимает вид: Изображение второй линии пересечения представлено на рисунке 3. Линия пересечения цилиндров равного радиуса в положительном.

Линия пересечения цилиндров равного радиуса.

Рис. 1. Линия пересечения двух цилиндров. Параметрическое уравнение первого цилиндра (рис. 1) имеет вид: (1). Линия пересечения цилиндров равного радиуса в положительном направлении оси Х представлена на рисунке 4.

Исследование свойств поверхностей вращения с использованием.

Поверхность, задаваемая уравнением , называется двуполостным гиперболоидом. Если поверхность пересечь плоскостями z=h, то линия пересечения определяется системой уравнений

Касательная. Задачи на касательную | Статья в журнале.

Составим уравнение касательной к графику заданной функции в точке : Так как эта прямая проходит через точку (2;3), то имеет место равенство , откуда находим: . Может ли касательная к кривой в какой-либо ее точке составлять острый угол с положительным направлением оси ?

Об определении некоторых геометрических параметров.

После решения системы уравнений (9) получим уравнение прямой D1D3

С целью определения точек пересечения линии наибольшего наклона плоскости S к горизонту, проходящую через т. D1, с периметром площади АВС, определим точки пересечения.

Математическое моделирование взаимодействия ионов.

Расположим дипольные частицы в плоскости цилиндра диаметром равном , ось цилиндра параллельна оси .

Проведём окружность с центром в точке Q и радиусом 2 см, находим точку пересечения

Тогда динамику движения частиц можно описать уравнениями системы (1–3).

Сечение поверхностей 2-го порядка общего вида по эллипсу.

Способ создания линии пересечения поверхностей вращения. Создание горизонтальной проекции линии пересечения по фронтальной проекции не является сложным.

Расчёт фундаментных плит методом конечных элементов

Построение линии пересечения двух цилиндров. Важным элементом такой модели является уравнение линии пересечения цилиндров. Из второго уравнения системы (4), на основании известных тригонометрических формул приведения.

Евклидова плоскость в четырехмерном пространстве

Построение линии пересечения двух цилиндров в параметрическом виде. Анализ и разработка измерительной установки для определения момента инерции тел вращения сложной формы.

🌟 Видео

Линия пересечения двух поверхностей вращения (Метод вспомогательных сфер)Скачать

Тело пересечения цилиндровСкачать

ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ДВУХ ЦИЛИНДРОВ. Начертательная геометрия [crossing two cylinders]Скачать

Лекция 12. Пересечение поверхностей метод плоскостейСкачать

Линия пересечения конуса и цилиндра (метод концентричных секущих сфер)Скачать

85КБ. Пересечение поверхностей цилиндра и полусферы. Определение видимости.Скачать

Построение линии пересечения поверхности цилиндра с проецирующей плоскостиСкачать

СОЕДИНЕНИЕ ЦИЛИНДРОВ В BLENDER/РАЗНЫЕ СПОСОБЫСкачать

Взаимное пересечение поверхностей/ (способ секущих плоскостей)/ Задача 49./ Рабочая тетрадь.Скачать

Задание 51. Как начертить ЛИНИЮ ПЕРЕСЕЧЕНИЯ ПРИЗМ.Скачать

36. Построение развертки цилиндра с линией пересеченияСкачать

VFXLAB || 3D ТРЮКИ. ПЕРЕСЕЧЕНИЕ ЦИЛИНДРОВ И ТРУБЫ.Скачать

Сперматозоид-чемпион | наглядно показано оплодотворениеСкачать