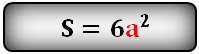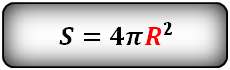Как найти площадь боковой поверхности конуса вписанного в цилиндр (7 видео)

Содержание

Все формулы для площадей полной и боковой поверхности тел
1. Площадь полной поверхности куба
2. Найти площадь поверхности прямоугольного параллелепипеда
3. Найти площадь поверхности шара, сферы
4. Найти площадь боковой и полной поверхности цилиндра
5. Площадь поверхности прямого, кругового конуса
Как найти площадь боковой поверхности конуса вписанного в цилиндр
📽️ Видео

Видео:ОТКУДА? Как найти площадь боковой поверхности конуса? Развёртка конуса | Математика с ДетекторомСкачать

Все формулы для площадей полной и боковой поверхности тел

Видео:Видеоурок по математике "Цилиндр"Скачать

1. Площадь полной поверхности куба

a — сторона куба

Формула площади поверхности куба,(S):

Видео:11 класс, 17 урок, Площадь поверхности конусаСкачать

2. Найти площадь поверхности прямоугольного параллелепипеда

a , b , c — стороны параллелепипеда

Формула площади поверхности параллелепипеда, (S):

Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

3. Найти площадь поверхности шара, сферы

R — радиус сферы

Формула площади поверхности шара (S):

Видео:ЗАДАНИЕ 8 из ЕГЭ_52Скачать

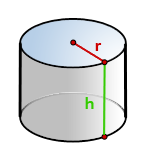
4. Найти площадь боковой и полной поверхности цилиндра

r — радиус основания

h — высота цилиндра

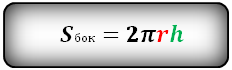
Формула площади боковой поверхности цилиндра, (S _бок ):

Формула площади всей поверхности цилиндра, (S):

Видео:ЗАДАНИЕ 8 из ЕГЭ_53Скачать

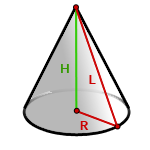
5. Площадь поверхности прямого, кругового конуса

R — радиус основания конуса

L — образующая конуса

Формула площади боковой поверхности конуса, через радиус ( R ) и образующую ( L ), (S _бок ):

Формула площади боковой поверхности конуса, через радиус ( R ) и высоту ( H ), (S _бок ):

Формула площади полной поверхности конуса, через радиус ( R ) и образующую ( L ), (S):

Формула площади полной поверхности конуса, через радиус ( R ) и высоту ( H ), (S):

Видео:62. Площадь поверхности конусаСкачать

Как найти площадь боковой поверхности конуса вписанного в цилиндр

Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 1:1, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса.

Исходный и отсеченный конус подобны с коэффициентом подобия 2. Площади поверхностей подобных тел относятся как квадрат коэффициента подобия. Поэтому площадь отсеченного конуса в 4 раза меньше площади поверхности исходного. Тем самым, она равна 3.

Полный конус и отсечённый конус имеют не пропорциональные полные поверхности:полный конус состоит из боковой поверхности+Sоснования, а отсечённый конус из Sбоковой и суммы двух оснований.

Отсечённый конус — это конус, а не усечённый конус.

Площадь полной поверхности конуса равна 108. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 1:1, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса.

Читайте также: Как посчитать воду в цилиндре

Площадь полной поверхности конуса равна 164. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 1:1, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса.

Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна Найдите площадь боковой поверхности конуса.

Заметим, что конус и цилиндр имеют общую высоту и равные радиусы основания. Площадь боковой поверхности цилиндра равна откуда, учитывая, что получаем: или

Образующая конуса его высота и радиус основания связаны соотношением откуда, учитывая, что получаем: или

Площадь боковой поверхности конуса равна следовательно:

Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.

Площадь основания конуса равна а площадь боковой поверхности Из условия имеем:

Значит, в прямоугольном треугольнике, образованном высотой, образующей и радиусом основания конуса, катет, равный радиусу, вдвое меньше гипотенузы. Тогда он лежит напротив угла 30°. Следовательно, угол между образующей конуса и плоскостью основания равен 60°.

Во сколько раз увеличится площадь боковой поверхности конуса, если его образующая увеличится в 3 раза, а радиус основания останется прежним?

Площадь боковой поверхности конуса равна где — длина окружности основания, а — образующая. При увеличении образующей в 3 раза площадь боковой поверхности конуса увеличится в 3 раза.

Во сколько раз увеличится площадь боковой поверхности конуса, если его образующая увеличится в 36 раз, а радиус основания останется прежним?

Читайте также: Блок цилиндров лифан х60

Площадь боковой поверхности конуса равна где — длина окружности основания, а — образующая. При увеличении образующей в 36 раз площадь боковой поверхности конуса увеличится в 36 раз.

Площадь боковой поверхности конуса в раз больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.

Площадь основания конуса равна а площадь боковой поверхности Из условия имеем:

Найдём косинус угла в прямоугольном треугольнике, образованном высотой, образующей и радиусом основания конуса: Значит, угол α равен 45°.

Аналоги к заданию № 27160: 509461 Все

Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшится в 1,5 раза, а образующая останется прежней?

Площадь боковой поверхности конуса равна где — радиус окружности в основании, а — образующая. Поэтому при уменьшении радиуса основания в 1,5 раза при неизменной величине образующей площадь боковой поверхности тоже уменьшится в 1,5 раза.

Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 8 раз, а образующая останется прежней?

Площадь боковой поверхности конуса равна где — радиус окружности в основании, а — образующая. Поэтому при уменьшении радиуса основания в 8 раз при неизменной величине образующей площадь боковой поверхности тоже уменьшится в 8 раз.

Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 15 раз, а образующая останется прежней?

Площадь боковой поверхности конуса равна где – радиус основания, а – образующая. Поэтому при уменьшении радиуса основания в 15 раз площадь боковой поверхности уменьшится тоже в 15 раз.

Длина окружности основания конуса равна 3, образующая равна 2. Найдите площадь боковой поверхности конуса.

Площадь боковой поверхности конуса равна где — длина окружности основания, а — образующая. Тогда

Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на

Найдем образующую по теореме Пифагора: Площадь полной поверхности конуса

Читайте также: Как отшлифовать тормозной цилиндр

Длина окружности основания конуса равна 7, образующая равна 2. Найдите площадь боковой поверхности конуса.

Площадь боковой поверхности конуса равна где — длина окружности основания, а — образующая. Тогда

Длина окружности основания конуса равна 6, образующая равна 2. Найдите площадь боковой поверхности конуса.

Площадь боковой поверхности конуса равна где – длина окружности основания, а – образующая. Тогда

Радиус основания конуса равен 12, высота равна 16. Найдите площадь полной поверхности конуса, деленную на π.

Найдем образующую по теореме Пифагора: Площадь полной поверхности конуса

Высота конуса равна 6, образующая равна 10. Найдите площадь его полной поверхности, деленную на

Площадь поверхности складывается из площади основания и площади боковой поверхности:

Радиус основания найдем по теореме Пифагора для треугольника, образованного высотой, образующей и радиусом: Тогда площадь поверхности

Высота конуса равна 20, образующая равна 25. Найдите площадь его полной поверхности, деленную на

Площадь поверхности складывается из площади основания и площади боковой поверхности:

Цилиндр и конус имеют общее основание, вершина конуса является центром другого основания цилиндра. Каждая образующая конуса наклонена к плоскости основания под углом 30°.

а) Докажите, что площади боковых поверхностей цилиндра и конуса равны

б) Найдите радиус сферы, касающейся боковых поверхностей цилиндра и конуса, а так

же одного из оснований цилиндра, если известно, что объем конуса равен

а) Пусть радиус основания цилиндра равен а высота Тогда тангенс угла наклона образующей есть откуда и образующая конуса равна Вычислим теперь площади боковой поверхности цилиндра и конуса. Это и что и требовалось доказать.

б) Рассмотрим сечение цилиндра и конуса осевой плоскость, проходящей через центр сферы. Все точки касания будут лежать в этой плоскости. В сечении получим окружность, вписанную в прямоугольный треугольник со сторонами поэтому ее радиус равен

C другой стороны, как мы знаем,

откуда поэтому искомый радиус равен 1.