- Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников
- Найдите площадь боковой поверхности правильной
- Как найти площадь боковой поверхности шестиугольной призмы описанной около цилиндра
- Найдите площадь боковой поверхности правильной шестиугольной
- Как найти площадь боковой поверхности шестиугольной призмы описанной около цилиндра
- 🌟 Видео
Видео:Стереометрия. ЕГЭ. Площадь боковой поверхности правильной шестиугольной призмыСкачать
Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников
Курс-тренинг Разбираем вариант 97 (1-14) —> Полный цикл видеоуроков по задачам 1-14 —> Полная В-подготовка (задачи 1-14) Полный цикл видеоуроков по задачам 1-14 При каком условии верно равенство 2990 + 1990 + 990 = 3900? —> Новые курсы: «EGE-мастер», «Достойный балл», «Ларинские варианты», «Раз-в-неделю», «Всё включено» —> Постоянно работают курсы для выпускников, учителей и репетиторов
12(B13). Площадь боковой поверхности правильной шестиугольной призмы (вар. 48)
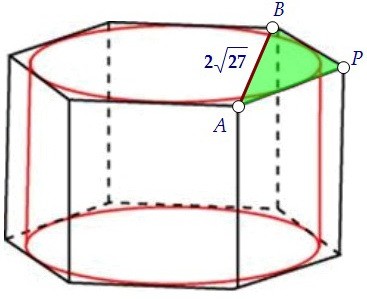
Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен √ 27 , а высота равна 1.
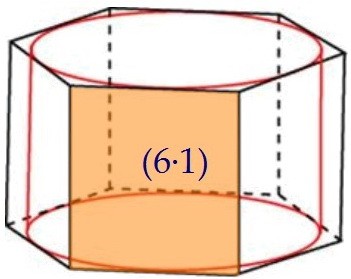
Площадь боковой поверхности правильной шестиугольной призмы состоит из площадей шести равных прямоугольников — боковых граней призмы: Sбок. = 6 · Sпрямоуг.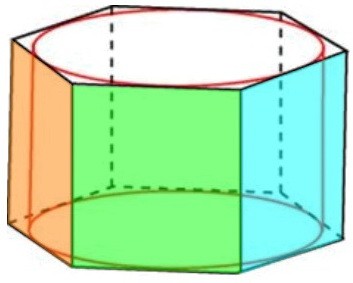 
Одна из сторон прямоугольника равна высоте вписанного цилиндра и дана по условию. Вторую сторону требуется найти. Иначе говоря, нам надо найти сторону шестиугольника. Дан радиус вписанного цилиндра, т.е. радиус вписанной в шестиугольник окружности. 
Диаметр этой окружности можно изобразить по-разному. Удобнее иметь дело с отрезком АВ. Треугольник АВР — равнобедренный (РВ = РА) с углом при вершине 120°. Основание в таком треугольнике в √ 3 раз больше боковой стороны, что полезно знать. 
Для подтверждения этого факта можно использовать теорему косинусов для стороны АВ: АВ 2 = а 2 + а 2 — 2 · а · а · cos120° АВ 2 = 2а 2 — 2а 2 · (-0,5) АВ 2 = 2а 2 + а 2 АВ 2 = 3а 2 AB = a√ 3 2√ 27 = a√ 3 6√ 3 = a√ 3 a = 6 Таким образом, одна сторона прямоугольника равна шести, вторая сторона равна единице. 
Площадь боковой грани равна 6 · 1 = 6, площадь боковой поверхности равна 6 · 6 = 36. Ответ: 36
Автор: Ольга Себедаш Просмотров: 70928
Курс-тренинг Разбираем вариант 97 (1-14) —> Полный цикл видеоуроков по задачам 1-14 —> Полная В-подготовка (задачи 1-14) Полный цикл видеоуроков по задачам 1-14 При каком условии верно равенство 2990 + 1990 + 990 = 3900? —> Новые курсы: «EGE-мастер», «Достойный балл», «Ларинские варианты», «Раз-в-неделю», «Всё включено» —> Постоянно работают курсы для выпускников, учителей и репетиторов
Комментарии к этой задаче:
Комментарий добавил(а): Ксюшинда
Дата: 2016-03-31
Спасибо большое. Всё понятно до невозможности)))))):)
Видео:Геометрия Найдите площадь боковой поверхности правильной треугольной призмы, описанной околоСкачать
Найдите площадь боковой поверхности правильной
27065. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен √3, а высота равна 2.
Площадь боковой поверхности данной призмы равна сумме площадей всех боковых граней. Так как дана правильная треугольная призма, то все три грани являются прямоугольниками, площади которых равны.
Для нахождения площади боковой грани необходимо знать её высоту и длину ребра основания. Высота дана. Найдём длину ребра основания. Рассмотрим проекцию (вид сверху:
Читайте также: Agb замки под цилиндр магнитный
Из прямоугольного треугольника АОС можем найти АС. По определению тангенса: Значит
Таким образом, сторона правильного треугольника выражается через радиус вписанной в него окружности как Значит площадь боковой поверхности будет равна: Ответ: 36
27066. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен √3, а высота равна 2.
Площадь боковой поверхности призмы равна произведению периметра снования и высоты. *Высота призмы равна высоте цилиндра. Вычислим сторону шестиугольника. Построим эскиз: Треугольник AOH равносторонний, Провели высоту OH, АН=НВ. Можем записать: Следовательно АВ=2. Таким образом, периметр шестиугольника равен 12, а искомая площадь 24 (периметр умножили на высоту призмы).
27107. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен 2√3, а высота равна 2.
Площадь боковой поверхности призмы равна: Сторона правильного треугольника выражается через радиус описанной окружности как: Тогда площадь боковой поверхности призмы равна: Ответ: 36
27064. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Диаметр цилиндра равен стороне квадрата лежащего в основании, это 2. Тогда периметр квадрата равен 8. Площадь боковой поверхности равна 8∙1=8.
Видео:ЕГЭ 2022 математика задача 4 вариант 2Скачать
Как найти площадь боковой поверхности шестиугольной призмы описанной около цилиндра
Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 2.
Площадь боковой поверхности фигуры равна сумме площадей всех боковых граней
Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 10.
Это задание ещё не решено, приводим решение прототипа.
Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота – 10.
площадь боковой поверхности фигуры равна сумме площадей всех боковых граней
Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 5.
Это задание ещё не решено, приводим решение прототипа.
Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота – 10.
площадь боковой поверхности фигуры равна сумме площадей всех боковых граней
Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 3, а высота — 10.
Это задание ещё не решено, приводим решение прототипа.
Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота – 10.
площадь боковой поверхности фигуры равна сумме площадей всех боковых граней
Видео:Найдите площадь боковой поверхности правильной шестиугольной призмыСкачать
Найдите площадь боковой поверхности правильной шестиугольной
27057. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 10.
Площадь боковой поверхности такой призмы равна сумме площадей ее боковых граней. У правильной шестиугольной призмы боковые грани равные прямоугольники со сторонами 5 и 10.
Читайте также: Площадь боковой поверхности цилиндра равна 100п см2
27066. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен , а высота равна 2.
Площадь боковой поверхности данной призмы равна сумме площадей всех боковых граней. Так как дана правильная шестиугольная призма, то все шесть граней являются прямоугольниками, площади которых равны.
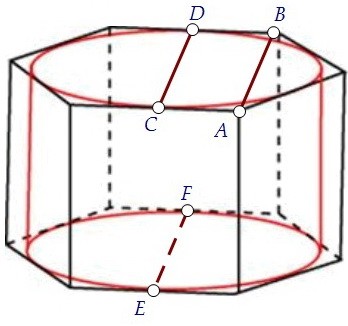
Для нахождения площади боковой стороны необходимо знать её высоту и длину ребра основания. Высота известна. Найдём длину ребра основания. Рассмотрим проекцию (вид сверху):
В прямоугольном треугольнике АВО известна АВ (это радиус цилиндра), ещё можем определить угол ОАВ, он равен 60 0 .
Воспользуемся определением тангенса прямоугольном треугольнике: Ребро АС равно 2АВ, так как ОВ является медианой, то есть делит АС пополам, значит: Таким образом, площадь боковой поверхности: Ответ: 24
Видео:Стереометрия. ЕГЭ. Найдите площадь боковой поверхности правильной шестиугольной призмыСкачать
Как найти площадь боковой поверхности шестиугольной призмы описанной около цилиндра
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Высота призмы равна высоте цилиндра, а сторона ее основания равна диаметру цилиндра. Боковые грани призмы — прямоугольники со сторонами 1 и 2. Поэтому площадь боковой поверхности 4 · 1 · 2 = 8.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 16. Найдите площадь боковой поверхности призмы.
Это задание ещё не решено, приводим решение прототипа.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Высота призмы равна высоте цилиндра, а сторона ее основания равна диаметру цилиндра. Боковые грани призмы — прямоугольники со сторонами 1 и 2. Поэтому площадь боковой поверхности 4 · 1 · 2 = 8.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Это задание ещё не решено, приводим решение прототипа.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Высота призмы равна высоте цилиндра, а сторона ее основания равна диаметру цилиндра. Боковые грани призмы — прямоугольники со сторонами 1 и 2. Поэтому площадь боковой поверхности 4 · 1 · 2 = 8.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 7. Найдите площадь боковой поверхности призмы.
Это задание ещё не решено, приводим решение прототипа.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Высота призмы равна высоте цилиндра, а сторона ее основания равна диаметру цилиндра. Боковые грани призмы — прямоугольники со сторонами 1 и 2. Поэтому площадь боковой поверхности 4 · 1 · 2 = 8.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 5,5. Найдите площадь боковой поверхности призмы.
Читайте также: Установка заднего тормозного цилиндра ваз 2109
Это задание ещё не решено, приводим решение прототипа.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Высота призмы равна высоте цилиндра, а сторона ее основания равна диаметру цилиндра. Боковые грани призмы — прямоугольники со сторонами 1 и 2. Поэтому площадь боковой поверхности 4 · 1 · 2 = 8.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 9. Найдите площадь боковой поверхности призмы.
Это задание ещё не решено, приводим решение прототипа.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Высота призмы равна высоте цилиндра, а сторона ее основания равна диаметру цилиндра. Боковые грани призмы — прямоугольники со сторонами 1 и 2. Поэтому площадь боковой поверхности 4 · 1 · 2 = 8.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 17. Найдите площадь боковой поверхности призмы.
Это задание ещё не решено, приводим решение прототипа.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Высота призмы равна высоте цилиндра, а сторона ее основания равна диаметру цилиндра. Боковые грани призмы — прямоугольники со сторонами 1 и 2. Поэтому площадь боковой поверхности 4 · 1 · 2 = 8.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 14. Найдите площадь боковой поверхности призмы.
Это задание ещё не решено, приводим решение прототипа.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Высота призмы равна высоте цилиндра, а сторона ее основания равна диаметру цилиндра. Боковые грани призмы — прямоугольники со сторонами 1 и 2. Поэтому площадь боковой поверхности 4 · 1 · 2 = 8.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 4. Найдите площадь боковой поверхности призмы.
Это задание ещё не решено, приводим решение прототипа.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Высота призмы равна высоте цилиндра, а сторона ее основания равна диаметру цилиндра. Боковые грани призмы — прямоугольники со сторонами 1 и 2. Поэтому площадь боковой поверхности 4 · 1 · 2 = 8.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 23,5. Найдите площадь боковой поверхности призмы.
Это задание ещё не решено, приводим решение прототипа.
Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
Высота призмы равна высоте цилиндра, а сторона ее основания равна диаметру цилиндра. Боковые грани призмы — прямоугольники со сторонами 1 и 2. Поэтому площадь боковой поверхности 4 · 1 · 2 = 8.
🌟 Видео
Площадь поверхности призмы. 11 класс.Скачать
Цилиндр вписан в четырехугольную призму. Найдите площадь боковой поверхности призмы.Скачать
ЕГЭ. Математика. База . Задача 16. Найдите площадь боковой поверхности правильной треугольной призмыСкачать
Стереометрия. ЕГЭ. Площадь боковой поверхности правильной треугольной призмыСкачать
КАК НАЙТИ ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПИРАМИДЫ?Скачать
#130. Задание 8: комбинация телСкачать
Площадь боковой поверхности правильной шестиугольной призмы#огэматематика #математикаСкачать
🔴 Стороны основания правильной шестиугольной ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать
Параллелепипед описан около цилиндраСкачать
ЕГЭ. Задача 8. Призма и цилиндрСкачать
Площадь полной поверхности призмыСкачать
Нахождение площади боковой поверхности цилиндраСкачать
ЕГЭ математика СТЕРЕОМЕТРИЯ 8#5.18🔴Скачать
11 класс, 15 урок, Площадь поверхности цилиндраСкачать
Призма и пирамида. Площадь и объем. Вебинар | Математика 10 классСкачать
