Как найти площадь боковой поверхности цилиндра если известна диагональ

Видео:Цилиндр - расчёт площади, объёма.Скачать

Цилиндр: площадь боковой поверхности. Формула площади боковой поверхности цилиндра

При изучении стереометрии одной из главных тем становится «Цилиндр». Площадь боковой поверхности считается если не главной, то немаловажной формулой при решении геометрических задач. Однако важно помнить и определения, которые помогут сориентироваться в примерах и при доказательстве различных теорем.

Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

Понятие цилиндра

Вначале нужно рассмотреть несколько определений. Только после их изучения можно приступать к рассмотрению вопроса о формуле площади боковой поверхности цилиндра. На основе этой записи можно вычислить и иные выражения.

• Под цилиндрической поверхностью понимают плоскость, описываемую образующей, движущейся и остающейся параллельной заданному направлению, скользящей по имеющейся кривой.
• Имеется и второе определение: цилиндрическую поверхность образуют множество параллельных прямых, пересекающих заданную кривую.
• Образующей называют условно высоту цилиндра. При ее перемещении вокруг оси, проходящей через центр основания, получается обозначенное геометрическое тело.
• Под осью подразумевают прямую, проходящую через оба основания фигуры.
• Цилиндром называется стереометрическое тело, ограниченное пересекающимися боковой поверхностью и 2 параллельными плоскостями.

Существуют разновидности данной объемной фигуры:

Видео:60. Площадь поверхности цилиндраСкачать

Условные обозначения

• Радиус основания – R (он же заменяет аналогичную величину стереометрической фигуры).
• Образующая – L.
• Высота – H.
• Площадь основания – Sосн (иначе говоря, необходимо найти указанный параметр круга).
• Высоты скошенного цилиндра – h1,h2 (минимальная и максимальная).
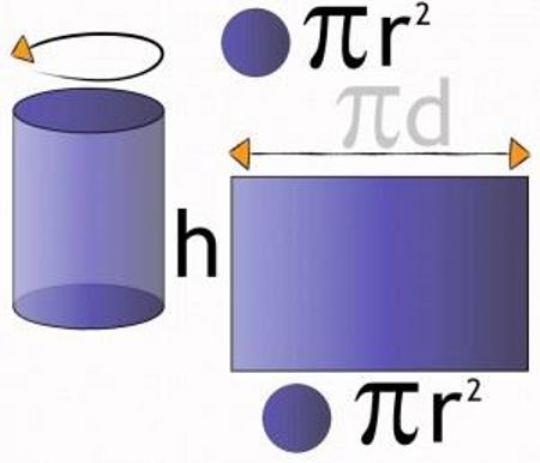
• Площадь боковой поверхности – Sбок (если ее развернуть, то получится своего рода прямоугольник).
• Объем стереометрической фигуры – V.
• Площадь полной поверхности – S.

Видео:Видеоурок по математике "Цилиндр"Скачать

«Компоненты» стереометрической фигуры

Когда изучается цилиндр, площадь боковой поверхности играет немаловажную роль. Связано это с тем, что данная формула входит в несколько других, более сложных. Поэтому необходимо быть хорошо подкованным в теории.

Основными составляющими фигуры являются:

Видео:Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндраСкачать

Основные формулы для работы с цилиндром

Для того чтобы ответить на вопрос, как найти площадь поверхности цилиндра, необходимо изучить основные «компоненты» стереометрической фигуры и формулы их нахождения.

Читайте также: Тепловая изоляция трубопровода цилиндр

Данные формулы отличаются тем, что вначале даются выражения для скошенного цилиндра, а затем – для прямого.

Видео:КАК НАЙТИ ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПИРАМИДЫ?Скачать

Примеры с разобранным решением

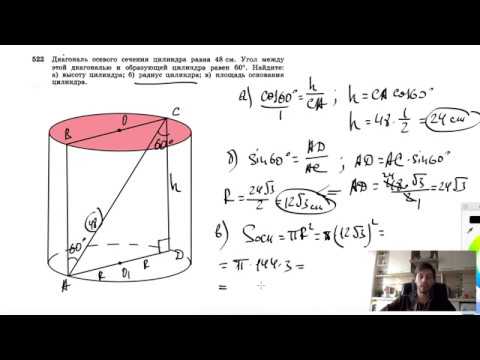
Необходимо узнать площадь боковой поверхности цилиндра. Дана диагональ сечения AC = 8 см (причем оно является осевым). При соприкосновении с образующей получается Решение. Поскольку известны величины диагонали и угла, то в таком случае: Комментарий. Треугольник ACD, в конкретном примере, прямоугольный. Это означает, что частное от деления CD и AC = косинусу имеющегося угла. Значение тригонометрических функций можно найти в специальной таблице. Аналогично, можно найти и значение AD: Теперь необходимо вычислить по следующей формулировке нужный результат: площадь боковой поверхности цилиндра равна удвоенному результату перемножения «пи», радиуса фигуры и ее высоты. Следует воспользоваться и другой формулой: площадью основания цилиндра. Она равняется результату перемножения «пи» на квадрат радиуса. И наконец, последняя формула: общая площадь поверхности. Она равна сумме предыдущих двух площадей. Даны цилиндры. Их объем = 128*п см³. У какого из цилиндров наименьшая полная поверхность? Решение. Для начала нужно воспользоваться формулами нахождения объема фигуры и ее высоты. Поскольку площадь полной поверхности цилиндра известна из теории, необходимо применить ее формулу. Если рассматривать полученную формулу в качестве функции площади цилиндра, то минимальный «показатель» будет достигнут в точке экстремума. Для получения последнего значения необходимо воспользоваться дифференцированием. Формулы можно посмотреть в специальной таблице по нахождению производных. В дальнейшем найденный результат приравнивается к нулю и находится решение уравнения. Ответ: Smin будет достигнута при h = 1/32 см, R = 64 см. Дана стереометрическая фигура – цилиндр и сечение. Последнее проведено таким образом, что располагается параллельно оси стереометрического тела. У цилиндра следующие параметры: ВК = 17 см, h = 15 см, R = 5 см. Необходимо найти расстояние между сечением и осью. Поскольку под сечением цилиндра понимается ВСКМ, т. е. прямоугольник, то его сторона ВМ = h. Необходимо рассмотреть ВМК. Треугольник является прямоугольным. Исходя из этого утверждения, можно вывести верное предположение, что МК = ВС. Отсюда можно сделать вывод, что МК = ВС = 8 см. Следующий шаг – проведение сечения через основание фигуры. Необходимо рассмотреть получившуюся плоскость. AD – диаметр стереометрической фигуры. Он параллелен сечению, упомянутому в условии задачи. BC – прямая, расположенная на плоскости имеющегося прямоугольника. ABCD – трапеция. В конкретном случае она считается равнобедренной, поскольку вокруг нее описана окружность. Если найти высоту полученной трапеции, то можно получить ответ, поставленный в начале задачи. А именно: нахождение расстояния между осью и проведенным сечением. Для этого необходимо найти величины AD и ОС. Ответ: сечение располагается 3 см от оси.

Видео:№523. Осевое сечение цилиндра — квадрат, диагональ которого равна 20 см. Найдите: а) высотуСкачать

Задачи на закрепление материала

Дан цилиндр. Площадь боковой поверхности используется в дальнейшем решении. Известны другие параметры. Площадь основания – Q, площадь осевого сечения – М. Необходимо найти S. Иными словами, полную площадь цилиндра. Дан цилиндр. Площадь боковой поверхности необходимо найти в одном из шагов решения задачи. Известно, что высота = 4 см, радиус = 2 см. Необходимо найти полную площадь стереометрической фигуры. Источник

Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Как найти площадь поверхности цилиндра: боковую, основания, полную

Видео:Как найти площадь боковой поверхности цилиндра #shorts #математика #геометрия #репетитор #огэ #егэСкачать

Площадь боковой поверхности цилиндра

Формула площади боковой поверхности цилиндра представляет собой произведение длины основания на его высоту:
Таким образом, используя формулы площади оснований и боковой поверхности фигуры, мы смогли найти полную площадь поверхности цилиндра.
Осевое сечение цилиндра представляет собой прямоугольник, в котором стороны равны высоте и диаметру цилиндра.
Формула площади осевого сечения цилиндра выводится из формулы расчета площади прямоугольника :

Видео:№543. Угол между диагоналями развертки боковой поверхности цилиндра равен φ, диагональ равна d.Скачать

Круговой цилиндр

где r – радиус основы, h – высота цилиндра, d – диаметр основы.

Видео:ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ ЦИЛИНДРАСкачать

Как рассчитать площадь боковой поверхности цилиндра с помощью калькулятора

1. внешний радиус и высота;
2. внешний диаметр и высота.

💡 Видео

Нахождение площади боковой поверхности цилиндраСкачать

№538. Площадь боковой поверхности цилиндра равна 5. Найдите площадь осевогоСкачать

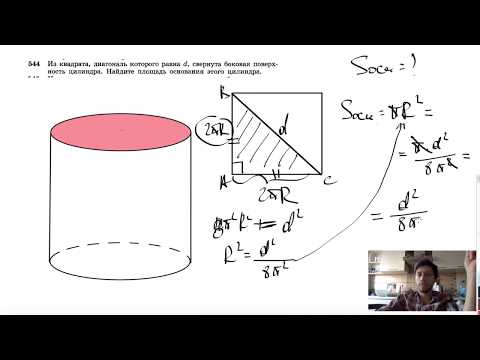
№544. Из квадрата, диагональ которого равна d, свернута боковая поверхность цилиндра.Скачать

Как найти площадь поверхности через диагональ куба? #509335Скачать

РЕШЕНИЕ ЗАДАЧ НА ЦИЛИНДРСкачать

Как находить площадь любой фигуры? Геометрия | МатематикаСкачать

Площадь поверхности призмы. 11 класс.Скачать

ПЛОЩАДЬ боковой поверхности ЦИЛИНДРАСкачать

№522. Диагональ осевого сечения цилиндра равна 48 см. Угол между этой диагональю и образующейСкачать