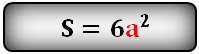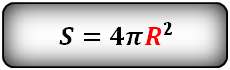- Все формулы для площадей полной и боковой поверхности тел
- 1. Площадь полной поверхности куба
- 2. Найти площадь поверхности прямоугольного параллелепипеда
- 3. Найти площадь поверхности шара, сферы
- 4. Найти площадь боковой и полной поверхности цилиндра
- 5. Площадь поверхности прямого, кругового конуса
- 5.5.6 Площадь поверхности конуса, цилиндра, сферы
- Нахождение площади поверхности конуса: формула и задачи
- Формула вычисления площади конуса
- 1. Боковая поверхность
- 2. Основание
- 3. Полная площадь
- Примеры задач
- Цилиндр, конус, шар
- Цилиндр, конус, шар
- Теорема Пифагора
- Формулы объема и площади поверхности. Цилиндр, конус и шар
- 🎬 Видео
Видео:Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шараСкачать

Все формулы для площадей полной и боковой поверхности тел
Видео:Шар вписан в цилиндр. Площадь поверхности шара равна 78. Найдите площадь полной поверхности цилиндраСкачать

1. Площадь полной поверхности куба
a — сторона куба
Формула площади поверхности куба,(S):
Видео:11 класс, 17 урок, Площадь поверхности конусаСкачать

2. Найти площадь поверхности прямоугольного параллелепипеда
a , b , c — стороны параллелепипеда
Формула площади поверхности параллелепипеда, (S):
Видео:Площадь полной поверхности цилиндраСкачать

3. Найти площадь поверхности шара, сферы
R — радиус сферы
Формула площади поверхности шара (S):
Видео:11 класс, 15 урок, Площадь поверхности цилиндраСкачать

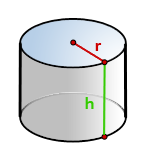
4. Найти площадь боковой и полной поверхности цилиндра
r — радиус основания
h — высота цилиндра
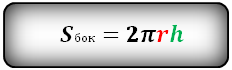
Формула площади боковой поверхности цилиндра, (S бок ):
Формула площади всей поверхности цилиндра, (S):
Видео:Как найти объем вписанного конуса? 🔍 #умскул_профильнаяматематика #умскул #никитасалливанСкачать

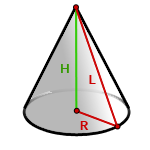
5. Площадь поверхности прямого, кругового конуса
R — радиус основания конуса
L — образующая конуса
Формула площади боковой поверхности конуса, через радиус ( R ) и образующую ( L ), (S бок ):
Формула площади боковой поверхности конуса, через радиус ( R ) и высоту ( H ), (S бок ):
Формула площади полной поверхности конуса, через радиус ( R ) и образующую ( L ), (S):
Формула площади полной поверхности конуса, через радиус ( R ) и высоту ( H ), (S):
Видео:Видеоурок по математике "Цилиндр"Скачать

5.5.6 Площадь поверхности конуса, цилиндра, сферы
Видеоурок: Объем и площадь поверхности тел вращения
Лекция: Площадь поверхности конуса, цилиндра, сферы
Поверхность цилиндра
Давайте вспомним, из чего состоит цилиндр – из боковой поверхности и двух оснований. Чтобы найти площадь всей боковой поверхности, следует найти площади каждой отдельной поверхности. Это значит, что для получения площади двух оснований (окружностей), следует воспользоваться формулой:
Двойка в формуле появилось из-за того, что у цилиндра два одинаковых основания. Поэтому вместо того, чтобы складывать две площади окружности, их достаточно просто умножить на «2».
С основаниями определились. Боковая поверхность цилиндра в развороте – это прямоугольник.
Площадь прямоугольника находится, как произведение смежных сторон. А так как одна из сторон описывает длину окружности основания, то можно воспользоваться формулой:
А значит, общая площадь поверхности цилиндра:
Поверхность конуса
Конус состоит из боковой поверхности, а также из основания в виде окружности. Для нахождения полной площади поверхности следует найти площадь каждой составляющей.
Площадь основания: S = πR 2
Площадь боковой поверхности: S = πRl , где l – образующая.
Следовательно, общая площадь поверхности конуса находится, как сумма площадей, описанных выше:
Поверхность сферы
Для нахождения площади поверхности шара необходимо воспользоваться формулой для площади круга, умножив её на «4»:
Для нахождения площади некоторого сегмента шара можно воспользоваться следующей формулой:
S = 2πRH , где Н – высота исследуемого сегмента.
Видео:ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ ЦИЛИНДРАСкачать

Нахождение площади поверхности конуса: формула и задачи
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь поверхности прямого кругового конуса (боковую, полную и основания), а также разберем примеры решения задач для закрепления материала.
Видео:Конус. 11 класс.Скачать

Формула вычисления площади конуса
1. Боковая поверхность
Площадь (S) боковой поверхности конуса равняется произведению числа π на радиус основания и на длину образующей.
Читайте также: Гелий в количестве находится в горизонтальном закрепленном цилиндре
Образующая ( l ) соединяет вершину конуса и границу основания, другими словами, точку на окружности.
Примечание: в вычислениях значение числа π округляется до 3,14.
2. Основание
Основанием конуса является круг, площадь которого вычисляется так:
Учитывая то, что диаметр круга равняется двум его радиусам ( d = 2R ), данную формулу можно представить в виде:
3. Полная площадь
Для вычисления суммарной площади конуса следует сложить площади боковой поверхности и основания:
Видео:62. Площадь поверхности конусаСкачать

Примеры задач
Задание 1
Вычислите площадь боковой поверхности конуса, если известно, что его радиус равен 16 см, а длина образующей – 5 см.
Решение:
Используем соответствующую формулу с известными нам величинами:
S = 3,14 ⋅ 16 см ⋅ 5 см = 251,2 см 2 .
Задание 2
Высота конуса равна 4 см, а его радиус – 3 см. Найдите суммарную площадь поверхности фигуры.
Решение:
Если рассмотреть конус в сечении, то можно заметить, что его высота, радиус и образующая представляют собой прямоугольный треугольник. Следовательно, воспользовавшись теоремой Пифагора, можно найти длину образующей (является гипотенузой):
l 2 = (4 см) 2 + (3 см) 2 = 25 см 2 .
l = 5 см.
Осталось только использовать найденное и известные по условиям задачи значения, чтобы рассчитать площадь:
S = 3,14 ⋅ 3 см ⋅ (5 см + 3 см) = 75,36 см 2 .
Видео:Шар вписан в цилиндр 5 задание проф. ЕГЭ по математикеСкачать

Цилиндр, конус, шар
Цилиндр, конус, шар
Цилиндр – тело, ограниченное цилиндрической поверхностью и двумя кругами с границами $М$ и $М_1$. Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.
Образующие цилиндрической поверхности называются образующими цилиндра, на рисунке образующая $L$.
Цилиндр называется прямым, если его образующие перпендикулярны основаниям. Осевое сечение цилиндра — это прямоугольник, у которого одна сторона равна диаметру основания, а вторая – высоте цилиндра.
Основные понятия и свойства цилиндра:
- Основания цилиндра равны и лежат в параллельных плоскостях.
- Все образующие цилиндра параллельны и равны.
- Радиусом цилиндра называется радиус его основания ($R$).
- Высотой цилиндра называется расстояние между плоскостями оснований (в прямом цилиндре высота равна образующей).
- Осью цилиндра называется отрезок, соединяющий центры оснований ($ОО_1$).
- Если радиус или диаметр цилиндра увеличить в n раз, то объем цилиндра увеличится в $n^2$ раз.
- Если высоту цилиндра увеличить в m раз, то объем цилиндра увеличится в то же количество раз.
- Если призму вписать в цилиндр, то ее основаниями будут являться равные многоугольники, вписанные в основание цилиндра, а боковые ребра — образующими цилиндра.
- Если цилиндр вписан в призму, то ее основания — равные многоугольники, описанные около оснований цилиндра. Плоскости граней призмы касаются боковой поверхности цилиндра.
- Если в цилиндр вписана сфера, то радиус сферы равен радиусу цилиндра и равен половине высоты цилиндра.
Площадь поверхности и объем цилиндра.
Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту.
Площадь поверхности цилиндра равна сумме двух площадей оснований и площади боковой поверхности.
Объем цилиндра равен произведению площади основания на высоту.
Объем части цилиндра, в основании которого лежит сектор: $V= / $, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.
Цилиндр описан около шара. Объём цилиндра равен $30$. Найдите объём шара.
Если в цилиндр вписан шар, то радиус цилиндра равен радиусу шара, а высота цилиндра в два раза больше радиуса шара.
Читайте также: Подъемный цилиндр кат 18343200
Распишем формулы объема цилиндра и шара.
Далее надо сравнить во сколько раз объем цилиндра больше объема шара, для этого разделим объемы друг на друга.
Объем цилиндра больше объема шара в $1.5$ раза, следовательно, чтобы найти объем шара, надо объем цилиндра разделить на $1.5$.
Конусом (круговым конусом) называется тело, которое состоит из круга, точки, не лежащей в плоскости этого круга, и всех отрезков, соединяющих заданную точку с точками круга.
Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими и обозначаются (l).
Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. Ось прямого конуса и его высота равны.
- Все образующие конуса равны.
- Осевым сечением конуса является равнобедренный треугольник, основание которого равно двум радиусам, а боковые стороны равны образующим конуса.
- Если боковая поверхность конуса – полукруг, то осевым сечением является равносторонний треугольник, угол при вершине равен $60°$.
- Если радиус или диаметр конуса увеличить в n раз, то его объем увеличится в $n^2$ раз.
- Если высоту конуса увеличить в m раз, то объем конуса увеличится в то же количество раз.
Площадь поверхности и объем конуса.
Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.
Площадь поверхности конуса равна сумме площади основания и площади боковой поверхности.
Объем конуса равен трети произведения площади основания на высоту.
Объем части конуса, в основании которого лежит сектор: $V= / $, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии ($R$) от данной точки (центра сферы $О$).
Тело, ограниченное сферой, называется шаром.
Осевое сечение шара это круг, радиус которого равен радиусу шара. Осевым сечением является самый большой круг шара.
Площадь поверхности сферы: $S_ =4π·R^2=π·d^2$, где $R$ — радиус сферы, $d$ — диаметр сферы
Объем шара: $V= / = / $, где $R$ — радиус шара, $d$ — диаметр шара.
Если радиус или диаметр шара увеличить в n раз, то площадь поверхности увеличится в $n^2$ раз, а объем в $n^3$ раз.
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$:
Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | $ / $ | $ / $ | $ / $ |
| $cosα$ | $ / $ | $ / $ | $ / $ |
| $tgα$ | $ / $ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | $ / $ |
Признаки подобия треугольников:
- Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Видео:11 класс. Геометрия. Объем цилиндра. 14.04.2020Скачать

Формулы объема и площади поверхности. Цилиндр, конус и шар
Тела вращения, изучаемые в школе, — это цилиндр, конус и шар.
Если в задаче на ЕГЭ по математике вам надо посчитать объем конуса или площадь сферы — считайте, что повезло.
Применяйте формулы объема и площади поверхности цилиндра, конуса и шара. Все они есть в нашей таблице. Учите наизусть. Отсюда начинается знание стереометрии.
Ты нашел то, что искал? Поделись с друзьями!
Смотрите также: Формулы объема и площади поверхности многогранников.
Кроме формул, в решении задач по стереометрии нужны также элементарная логика и пространственное воображение. Есть и свои небольшие секреты.
Например, такой важный факт:
Если все линейные размеры объемного тела увеличить в 2 раза, то площадь его поверхности увеличится в 4 раза, а объем — в 8 раз.
Вот такая задача. Как и остальные на нашем сайте, она взята из банка заданий ФИПИ.
1. Объем конуса равен . Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Очевидно, что объем меньшего конуса в раз меньше объема большого и равен двум.
Для решения некоторых задач полезны начальные знания стереометрии. Например — что такое правильная пирамида или прямая призма. Полезно помнить, что у цилиндра, конуса и шара есть еще общее название — тела вращения. Что сферой называется поверхность шара. А, например, фраза «образующая конуса наклонена к плоскости основания под углом 30 градусов предполагает, что вы знаете, что такое угол между прямой и плоскостью. Вам также может пригодиться теорема Пифагора и простые формулы площадей фигур.
Иногда неплохо нарисовать вид сверху. Или, как в этой задаче, — снизу.
2. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?
Всё просто — рисуем вид снизу. Видим, что радиус большего круга в раз больше, чем радиус меньшего. Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в раза больше.
Говорят, что хороший чертеж — это уже половина решения. Читайте о том, как строить чертежи в задачах по стереометрии.
Еще один важный момент. Помним, что в задачах части В вариантов ЕГЭ по математике ответ записывается в виде целого числа или конечной десятичной дроби. Поэтому никаких или у вас в ответе в части В быть не должно. Подставлять приближенное значение числа тоже не нужно! Оно обязательно должно сократиться!. Именно для этого в некоторых задачах задание формулируется, например, так: «Найдите площадь боковой поверхности цилиндра, деленную на ».
А где же еще применяются формулы объема и площади поверхности тел вращения? Конечно же, в задаче 14 Профильного ЕГЭ по математике.
Мы тоже расскажем о ней.
🎬 Видео
ЕГЭ 2022 математика задача 4 вариант 2Скачать

ОТКУДА? Как найти площадь боковой поверхности конуса? Развёртка конуса | Математика с ДетекторомСкачать

Цилиндр, конус, шар, 6 классСкачать

Цилиндр - расчёт площади, объёма.Скачать

Цилиндр и конус имеют общее основание и высоту. Высота цилиндра равна радиусу основания... (ЕГЭ)Скачать

ЗАДАНИЕ 8 из ЕГЭ_53Скачать

Площадь осевого сечения цилиндра равна 4. Найдите площадь боковой поверхности цилиндраСкачать